Собственное поглощение света

Оператор Гамильтона для электронов полупроводника, находящегося в световом поле, имеет вид

,

где - оператор энергии электрона в электромагнитном поле.

Под действием электромагнитного излучения могут происходить переходы электронов между стационарными состояниями в кристалле. Вероятность перехода можно получить, пользуясь теорией возмущений:

 

Где ψ _i (r,t) = ψ_1к1(r,t): – волновая функция электрона в валентной зоне с энергией E₁(к₁), ему соответствует волновая функция:

;

 

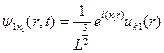ψ _f (r,t) = ψ_2к2(r,t)– волновая функция электрона в зоне проводимости с энергией E₂(к₂) и волновой функцией:

Рассмотрим возмущение , индуцирующее переходы из одного состояния в другое. В качестве возмущения мы берем энергию электрона в поле световой волны, которую можно характеризовать напряженностью E электрического поля и индукцией B магнитного поля.

Запишем уравнения Максвелла (в системе Гаусса) для случая, когда отсутствует сторонние поля и объемные заряды:

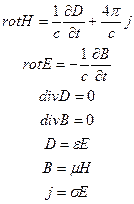
Вместо двух величин удобно ввести векторный потенциал A (r,t), который позволяет выразить через него E и B (в системе Гаусса):

Гамильтониан электрона в кристалле, находящемся в поле электромагнитной волны, в приближении эффективной массы имеет вид

Если ограничиться слабыми световыми потоками, которые можно получить от обычных источников света, то последний член, пропорциональный А², по сравнению с линейным членом можно отбросить. Учитывая, что векторный потенциал должен удовлетворять условию Лоренца:

divA=0,

выделим оператор возмущения

где,

Чтобы вычислить вероятность перехода, необходимо задать возмущение . Пусть кристалл взаимодействует с линейно-поляризованной монохроматической электромагнитной волной, тогда векторный потенциал также представляет собой плоскую волну:

A(r,t)=A₀e^i(ωt-(gr))

Для оператора возмущения имеем

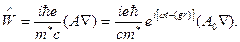
Вычислим матричный элемент перехода с помощью волновых функций Блоха ψ_1к1(r,t) и ψ_2к2(r,t):

Этот матричный элемент отличен от нуля только в том случае, когда

к₁+g=к₂

или

P₂=P₁+ћg,

т.е. при поглощении света должен выполняться закон сохранения квазиимпульса: квазиимпульс состояния равен векторной сумме квазиимпульса начального состояния и импульса фотона.

Если k₁=0, то k₂=g. Но такие переходы невозможны, поскольку в этом случае (А₀к₂)=(А₀g)=0 (условие поперечности световой волны). Квазиимпульс электронов с тепловой энергией имеет 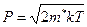. При T=300К и m^*=10^-27г имеем P≈10^-20г∙см/сек и к≈10⁷см^-1. Для света с длиной волны , что значительно меньше к для тепловых электронов. В таком случае, пренебрегая величиной ћg по сравнения с P₁, получим правила отбора

P₂=P₁; к₁=к₂.

Переходы из валентной зоны в зону проводимости в соответствии с правилами отбора – с сохранением волнового вектора электрона – носят название прямых, или вертикальных. Электрон, поглотив фотон, переходит из некоторой точки зоны Бриллюэна валентной зоны в эквивалентную точку зоны Бриллюэна зоны проводимости.

Матричный элемент оператора возмущения входит член . При вычислении вероятности перехода в единицу времени этот множитель дает δ-функцию

,

которая отражает факт выполнения закона сохранения энергии и при поглощении света:

Вероятность перехода электрона из единичного объема к₁-пространства в единичный объем к₂-пространства в единицу времени равна

Предполагая в дальнейшем, что закон сохранения энергии и квазиимпульса выполняются, мы можем опустить δ-функцию.

Выразим вероятность перехода электрона через число фотонов, проходящих через полупроводник. Для этого учтем, что средняя плотность световой энергии равна 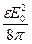(мгновенная плотность равна ), поток энергии равен , где n - коэффициент преломления вещества и 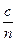- скорость света в нем. Поток фотонов q найдем, если поток энергии разделим на энергию одного фотона:

.

Найдем связь между А₀ и E₀:

и

отсюда следует

или

.

В итоге для вероятности перехода имеем

.

Переход электрона из одного состояния в другое возможен только в результате поглощения фотонов, поэтому есть вероятность поглощения фотонов. Так как она пропорциональна потоку фотонов q, то эффективное сечение поглощения однофотонного потока на одном электроне мы получим, разделив на поток фотонов q:

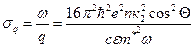
Оценим величину эффективного сечения поглощения однофотонного потока электроном, предположив, что m^*=10^-27г, ε≈16, n≈4, к₂≈10⁷см^-1 при ω≈10¹⁴сек^-1 и cos²Θ=1/3, получим σ_q=10^-26cм². Это значение соответствует площади поперечного сечения электрона в классической физике.

Если рассматривать вероятность, отнесенную к одному фотону, который образует поток 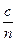, то

.

 

Перейдем к нахождению коэффициента поглощения α. В элементе объема имеется свободных и занятых состояний. В этом элементе объема имеется занятых и свободных состояний. Поскольку вероятность прямых и обратных переходов равна, то при вычислении коэффициента поглощения света необходимо учитывать как прямые, так и обратные переходы, вызванные светом. Спонтанными переходами (рекомбинационными переходами) мы будем при этом пренебрегать. За единицу времени будет поглощено фотонов

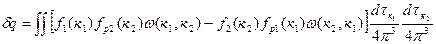
Первый член в этом выражении определяет число поглощенных фотонов, второй – излученных. В обычных условиях уровни энергии заняты электронами в соответствии с равновесным распределением их по состояниям:

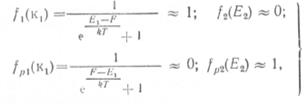
т.е. валентная зона практически заполнена, а зона проводимости практически свободна, поэтому обратными переходами можно пренебречь (но если в полупроводнике создать инверсную заселенность уровней, то такой полупроводник будет усиливать излучение, а не поглощать). Умножим на ћω, получим количество энергии, поглощаемой в единице объема в единицу времени:

.

Интегрируя с учетом , получим

Исключим зависимость α от E₁, E₂ и , учитывая, что величина эффективной массы m^*, входящая во все выражения, есть эффективная масса электрона в валентной зоне, или масса дырки. Выразим через ω:

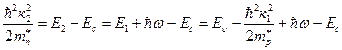
При к₁=к₂ имеем

где

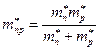
- приведенная эффективная масса электрона и дырки.

Не зависящий от времени матричный элемент перехода можно вычислить с помощью выражения

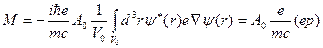
где 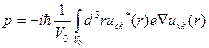- матричный элемент перехода для импульса

Пользуясь тем, что при комнатных температурах в полупроводнике зона проводимости свободна, а валентная зона практически заполнена, можно утверждать, что число поглощенных фотонов в единицу времени на единицу площади равно числу переходов, следовательно, вероятность перехода:

Коэффициент поглощения дается выражением:

Так как мы интересуемся спектральной зависимостью коэффициента поглощения вблизи края собственного поглощения, то рассматриваем переходы между состояниями, находящимися вблизи экстремумов разрешенных зон. Матричный элемент перехода для импульса в этом случае можно представить в виде ряда:

.

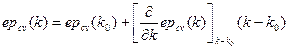Если , переход называется разрешенным. Ограничиваясь в этом случае первым членом ряда, получим

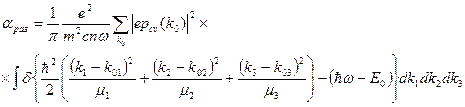
где - сумма значений для всех точек, соответствующих рассматриваемым экстремумам в зоне Бриллюэна.

Переходя к переменным интегрирования 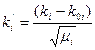, получим

,

где мы положили . Вводя переменную интегрирования и используя δ-функцию, получим

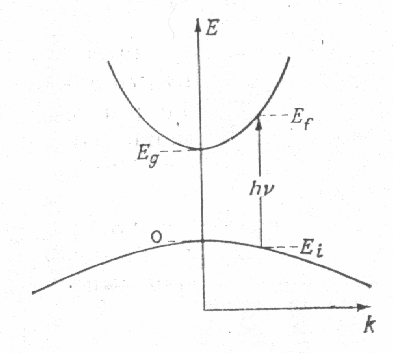
Рис 2. Зонная схема вблизи экстремумов для прямозонного полупроводника.

 

Рассмотрим, как α зависит от используемой модели зон. Если в полупроводнике экстремумы находятся в центре зоны Бриллюэна, то для скалярной эффективной массы имеем: 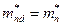; 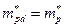. Так как вероятность перехода отлична от нуля в том случае, если выполняется закон сохранения энергии, то α можно выразить через N ₁(E) и N₂ (E₂) – функции плотности состояний дырки и электрона в валентной зоне и зоне проводимости соответственно:

и

Получим, что коэффициент поглощения является функцией

.

Согласно правилам отбора переходы могут быть, в дипольном приближении, разрешенными и запрещенными. Для запрещенных переходов, ряда 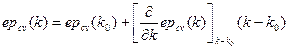будет равно нулю, поэтому разложение начинается со второго члена, что дает в результате зависимость:

.

Если , то α=0 – собственное поглощение имеет резкую границу со стороны малых частот. Граница собственного поглощения определяется (оптической) шириной запрещенной зоны для вертикальных переходов:

; .

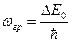Если выразить ширину запрещенной зоны в эВ, то граница собственного поглощения можно вычислить из соотношения:

.

Выражение на α справедливо только при переходах в полупроводниках со сферическими поверхностями энергии и экстремумами, лежащими в центре зоны Бриллюэна.

Таким образом, прямые переходы должны давать зависимость α от в виде:

Где r может принимать значения от ¹/₂ до ³/₂ при прямых, а 2, 3 при не вертикальных переходах. Граница поглощения определяет оптическую ширину запрещенной зоны , которая превосходит минимальное расстояние между валентной зоной и зоной проводимости, определяющее термическое возбуждение электронов.

Поскольку существует состояния, разделенные энергетическими промежутками меньшими, чем 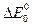, то возникает вопрос, возможно ли поглощение фотона с энергией меньшей, чем . Очевидно, что при этом правила отбора к₁+g=к₂, P2=P₁+ћg должны нарушаться. Однако нарушение правил отбора к₁+g=к₂ не может означать нарушения законы сохранения квазиимпульса (импульса). Переход электрона из состояния к₁≈0 в состояние к₂≈к₀ возможен, если изменение импульса электрона будет компенсироваться изменением импульса фотона.

Рассмотрим две возможности. Первая:

Электрон переходит из состояния E₁ (0) в состояние E₂ (к₀) в результате поглощения фотона с энергией 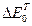длинноволнового фотона с энергией , при этом электрон оказывается в состоянии E₂ (0). Испустив фотон с энергией и волновым вектором - к₀, электрон оказывается в состоянии E₂ (к₀). Таким образом, электрон переходит из E₁ (0) в E₂ (к₀), поглотив фотон с энергией . Необходимая для переброса электрона энергия сообщается электрону решеткой, и решетке же она передается электроном. Переход электрона происходит через промежуточное состояние, в котором происходит преобразование длинноволнового фотона в коротковолновой. Другими словами, переход электрона из зоны проводимости в валентную зону происходит за счет энергии фотона, изменение же импульса электрона компенсируется решеткой (фононом).

Разобранная выше схема не является единственно возможной. Действительно, электрон в состоянии E₁ (0) может поглотить фонон с энергией и квазиимпульсом ћк₀, в результате чего он окажется в некотором виртуальном состоянии; испустив длинноволновой фотон с энергией , электрон окажется в состоянии E₂ (к₀). Электрон в состоянии E₁ (0) может испустить фонон с энергией и импульсом (-ћк₀) и оказаться при этом в некотором виртуальном состоянии, поглотив затем фотон с энергией 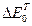, электрон окажется в состоянии E₂ (к₀). Таким образом, переход электрона из состояния E₁ (0) в состояние E₂ (к₀) при к₁≈0 и к₂≈к₀ происходит через ряд виртуальных состояний. Чтобы получить зависимость α(ω), необходимо учесть законы сохранения энергии и импульса

,

,

где ω_фон, К_фон – частота и волновой вектор поглощаемого (плюс) и испускаемого (минус) фотона. Граница поглощения должна определяться условием

.

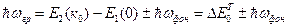Таким образом, существуют две границы собственного поглощения, оптическая ширина запрещенной зоны (минимальная) при непрямых невертикальных переходах должна быть меньше термической ширины запрещенной зоны 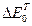на энергию фонона .

Если предположить, что возмущение содержит теперь некоторую характеристику фононов, то вероятность перехода электрона будет определяться как матричным элементом возмущения со стороны электромагнитного поля, так и матричным элементом возмущения со стороны решетки.

В предположении, что матричный элемент возмущения со стороны решетки не зависит от частоты фонона, мы получим зависимость коэффициента поглощения от частоты в виде

.

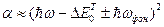Если учесть, что число фононов зависит от их энергии и температуры, то выражение для α можно записать в виде

Первый член описывает процесс поглощения света с поглощением фононов, число которых пропорционально величине , второй член описывает процесс поглощения фотона с испусканием фонона, вероятность испускания фонона равна вероятности того, что данное колебание состояние не возбудило, т.е.

.

Рис. 3. Зонная схема вблизи экстремумов зон Бриллюэна для непрямозонного полупроводника.

В заключение этого рассмотрения, сравним коэффициенты поглощения света в результате прямых и непрямых переходов. Прямой переход определяется вероятностью встречи двух частиц – электрона и фотона. При непрямых переходах должны встретиться три частицы – электрон, фотон и фонон. Но это означает, что непрямой переход является процессом менее вероятным, чем прямой, поэтому коэффициент поглощения света при прямых переходах должен достичь больших величин, чем для непрямых переходов. Таким образом:

1. Переходы электрона при поглощении света называются прямыми, или вертикальными, если выполняется правило отбора к₁+g=к₂, или к₁=к₂. Переходы называются непрямыми, или невертикальными, если .

2. Край собственного поглощения определяется при прямых и непрямых переходах соответственно соотношениями: , .

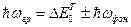3. Коэффициент поглощения α у края собственного поглощения пропорционален разности в степени r: 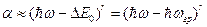где r принимает значения от ¹/₂ до 3 в зависимости от структуры зон энергии.

4. Собственное поглощение приводит к генерации пары свободных носителей заряда – электрон и дырка.

5. Собственное поглощение приводит к быстрому поглощению света; длина свободного пробега фотона l_фт при имеет величину порядка .

 

Экситон

Определение экситона

В полупроводниках и диэлектриках возможно поглощение света, которое не сопровождается появлением свободных носителей заряда. Возникающее возбуждение является электрически нейтральным и может быть рассмотрено как квазичастица, состоящая из электрона и дырки и называемая экситоном. Понятие «экситон» было введено Я.И.Френкелем в 1931 г. при теоретическом исследовании превращения света в тепло в твердых телах. Используя модель простейшего молекулярного кристалла, образованного атомами инертных газов, он рассмотрел коллективные возбужденные состояния кристалла, обусловленные резонансными взаимодействиями между возбужденными и невозбужденными атомами. Понятие экситона было введено Френкелем при интерпретации некоторых спектров кристаллов; в этом случае пара электрон - дырка рассматривается, как некая частица, которая может перемещаться по кристаллу в результате взаимодействий узлов решетки.

Возможность возникновения дополнительных волн в кристалле вблизи частот экситонного поглощения была показана Пекаром в 1957 г. с использованием микроскопического подхода для описания возбужденных экситонных состояний кристалла. Феноменологический подход к описанию электродинамики кристаллических сред с пространственной дисперсией был развит в работах Аграновича, Гинзбурга и Рухадзе. Вследствие зависимости тензора диэлектрической проницаемости среды от показателя преломления N степень основного уравнения кристаллооптики относительно N² становится выше второй и зависит как от структуры кристалла, так и от направления распространения волны. Это приводит к возникновению в кристалле окрестности экситонного резонанса дополнительной поперечной волны той же частоты и поляризации, что и основная волна вне области резонанса, но с другим значением показателя преломления.

В полупроводниках экситон был обнаружен в 1951 г. Е.Ф.Гроссом с сотрудниками. Было получено прямое экспериментальное доказательство существования экситонов в кристаллической решетке. Прямыми опытами был обнаружен водородоподобный оптический спектр экситона, спектр его образования и спектр его аннигиляции.

Рис 4. Спектр поглощения кристаллической закиси меди Cu₂O

Пики на Рис4. соответствуют энергетическим уровням экситонам закиси меди.

Этими опытами было установлено, что в некоторых кристаллах частоты линий спектра энергетических уровней экситонных возбужденных состояний образуют водородоподобные серии. Это показывало, что электрические заряды, входящие в состав образования (экситона), дающего водородоподобную серию линий в спектре, связаны силами Кулона. Отсюда следовало, что действительно в кристаллах экситон может существовать, как водородоподобный квазиатом, состоящий из электрона и дырки, связанных кулоновским притяжением, движущийся в кристаллической решетке, как целое.

Основным свойством экситона является его способность перемещаться в решетке. Именно благодаря этому важному свойству так велика роль экситонов в различных процессах, происходящих в кристаллах. Изучению движения экситонов посвящено большое число экспериментальных работ. Эти работы главным образом касаются переноса энергии экситонами в органических кристаллах.

Согласно представлениям зонной теории при возбуждении электронной системы полупроводника образуются пары свободных электронов и дырок. Г.Ваннье и Н.Мотт обратили внимание на то, что благодаря кулоновскому взаимодействию электронно-дырочная пара может иметь связанные состояния, образуя водородоподобную систему - экситоны большого радиуса (экситон Ваннье-Мотта). Для случая простых параболических зон в кубическом кристалле уравнение для нахождения как связанных, так и несвязанных состояний экситона имеет вид

,

где М=m_e+m_h – трансляционная масса экситона, - приведенная масса, - определяет координату центра масс электронно-дырочной пары, радиус-вектор относительно движения электрона и дырки, E - полная энергия экситона.

Используем метод разделения переменных. Для связанных состояний решение может быть представлено в виде

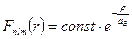- волновая функция водородоподобного атома, имеющего эффективный заряд ; n, l, m -квантовые числа, характеризующие внутреннее состояние водородоподобной системы, - радиус Бора, - волновой вектор поступательного движения экситона.

Энергия, которой обладает экситон в связанном состоянии, удовлетворяет уравнению

Большая величина радиуса экситона по сравнению с постоянной решетки дает возможность пользоваться приближением эффективной массы, в рамках которого и выводится уравнение.

 

Рис. 5: Дискретный и сплошной спектры экситона с учетом его кинетической энергии.

Пунктир в Рис. 5 – дисперсия света в среде.

На Рис.5 изображена энергетическая схема состояний, описываемая формулой энергии экситона. Цифры 1; 2;..∞ -значения главного квантового числа n; n=∞ соответствует краю сплошного спектра. Рождение экситона возможно в акте поглощения кванта света при выполнении законов сохранения волнового вектора и энергии. На рис.5 этим условиям соответствуют точки пересечения линии световой дисперсии (с учетом коэффициента преломления света в среде) с дисперсионными ветвями экситона. В соответствии со схемой рис.5 в спектре поглощения (пропускания) света достаточно тонких образцов должна наблюдаться серия линий, сходящихся в коротковолновую сторону и переходящая в сплошной спектр. После открытия такой серии в закиси меди экситон большого радиуса был зарегистрирован практически во всех полупроводниках.

 

Поглощение

Точное рассмотрение взаимодействия света с экситонами приводит к дальнейшему усложнению энергетического спектра дипольно-активных экситонов. Поскольку свет, распространяющийся по кристаллу, является поперечной волной вторичной поляризации, то в области резонанса световые волны должны сильно взаимодействовать с поперечными волнами экситонной поляризации и смешиваться с ними. В результате взаимодействия света с поперечными экситонами в кристалле происходит образование новых элементарных возбуждений – свето-экситонов (поляритонов).

Уравнения Максвелла дают следующую связь между индукцией D и поперечной компонентой поля :

При совместном решении данного уравнения и материального уравнения получаем дисперсионное соотношение:

Далее, используя выражение для диэлектрической проницаемости

можно найти и конкретный вид дисперсионной зависимости для поперечных поляритонов Рис. 6. Для среды с пространственной дисперсией диэлектрическая проницаемость выражается как: и закон дисперсии принимает вид:

,

где , , где Г – константа затухания, ε ₀-фоновая диэлектрическая проницаемость, обусловленная другими возбуждениями кристалла, ω₀-резонансная частота. Две ветви решения T₁ и T₂ соответствуют возбуждениям свето-экситонов и называются поляритонами.

Ход дисперсионных ветвей T₁ и T₂ в области «антипересечения» показывает, что свето-экситонам примерно в одинаковой степени присущи как свойства фотонов, так и свойства экситонов. Вследствие этого процессы поглощения и излучения света экситонами определяются динамикой поляритонов в области резонанса. Продольные экситоны (L) не участвуют в свето-экситонном взаимодействии с поперечными световыми колебаниями, поэтому дисперсия ветви продольных экситонов не изменяется.

Дисперсионная зависимость экситона представлена на Рис 6.

Рис. 6. Дисперсионная кривая экситона при учете взаимодействия поперечного поля с полем поперечного экситона.