Пример
Если в одном и том же круге центральные углы равны, то равны и соответствующие им дуги.
Если в одном и том же круге дуги равны, то равны и соответствующие им центральные углы
2. Числовая функция и ее график. Определения: композиции функций, обратной функция. График обратной функции. Основные элементарные функции и их графики. Определение элементарной функции.
Числовая функция -функция, у которой область определения и множество значений являются числовыми множествами.
График числовой функции — это множество точек плоскости с координатами (x, f(x)), когда x принимает всевозможные значения из области определения функции f
Компози́ция фу́нкций — это применение одной функции к результату другой.
Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией
Если у нас будет задан график некоторой обратимой функции f, то для того чтобы построить график обратной функции, можно пользоваться следующим утверждением: график функции f и обратной к ней функции g будут симметричны относительно прямой, заданной уравнением y = x.
Элементарной функцией называется функция, которая может быть задана в виде y = f (x), где справа стоящее выражение составлено из основных элементарных функций, постоянных при помощи конечных операций сложения, вычитания, умножения, деления и взятия функции от функции.
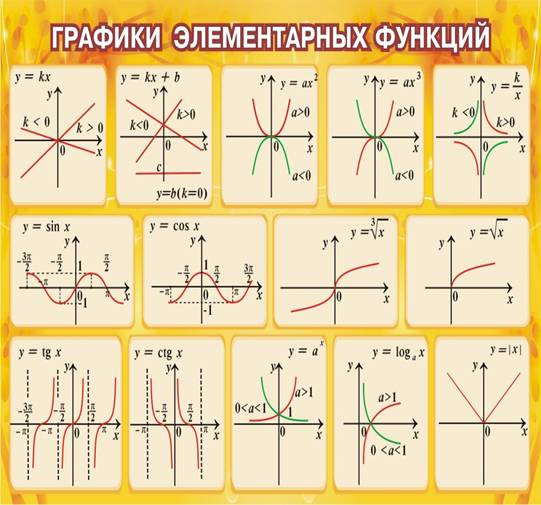 |
3. Определение предела последовательности, геометрическая интерпретация предела. Определение сходящейся последовательности. Общие свойства предела последовательности: предел постоянной, единственность предела, арифметические теоремы (о пределе константы, суммы, разности, произведения и частного двух последовательностей). Необходимое условие сходимости последовательности (ограниченность), достаточное условие сходимости последовательности (монотонность и ограниченность). Число е. Натуральные логарифмы. Определение гиперболических функций, основное гиперболическое тождество.
ОПРЕДЕЛЕНИЕ. Число a∈ℝ называется пределом последовательности { xn } если ∀ε>0 ∃N∈ℕ такое, что | xn – a | <ε, ∀n>N.
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ предела последовательности Пусть r ∈ ℝ, M(r) ∈Ox M(r) – геометрическая интерпретация числа r ∈ ℝ. Пусть x 0 ∈ ℝ, ε>0. Интервал (x 0 – ε; x 0 + ε) называют ε -окрестностью точки x 0. (геометрическое определение ε -окрестности точки)
если { x n } → a, то с геометрической точки зрения это означает, что в любой ε -окрестности точки a находятся все члены последовательности { x n}, за исключением может быть конечного их числа. (Геометрическая интерпретация предела последовательности).
Последовательность, имеющую предел, называют сходящейся (сходящейся к a)
Свойство 1. Постоянный множитель c можно выносить за знак предела:
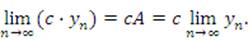
Свойство 2. Если существуют конечные пределы последовательностей  и
и 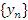 , то
, то
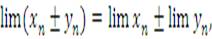


Свойство 3. Если существуют конечные пределы последовательностей 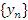 и
и  , то
, то
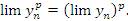
Предел постоянной равен самой постоянной
Единственность предела. Если последовательность сходится, то она имеет только один предел.
Предел суммы
Предел суммы равен сумме пределов, если каждый из них существует, т.е.
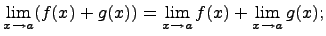
Предел разности
Предел разности равен разности пределов, если каждый из них существует, т.е.

Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
