1. Нелинейная система устойчива в «малом», то есть при малых начальных отклонениях, если отрицательны все вещественные части корней характеристического уравнения системы, составленного для ее линейного приближения.
2. Нелинейная система неустойчива в «малом», если хотя бы одна вещественная часть корня характеристического уравнения ее линейного приближения положительна.
При наличии чисто мнимых корней указанного уравнения вопрос об устойчивости системы требует в каждом случае дополнительного исследования.
БИЛЕТ№11
Общий вид кривых Перла, описываемых математической функцией времени, приведен на рис. 2.1.
Логистическая функция описывается уравнением вида [4, 7]:
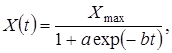(2.1)
 X
   
   
   t
0 t 1 ln a/b t2
|
где 
– численность популяции в единице объема выпуска системы в момент времени t; 
– максимальная численность популяции; a, b – константы.
Из рис. 2.1 видно, что логистическая кривая начинается в точке 
, симметрична и имеет точку перегиба с координатами
| Рис. 2.1 |
Константа a определяет положение логистической кривой по времени (сдвиг влево или вправо), константа b – наклон кривой. Эти константы очень легко вычисляются по формулам:
. (2.2)
При известном времени удвоения биологических популяций t 1/2 константу b можно определить по формуле
(2.3)
Логистическая функция обладает одним замечательным свойством – на ней можно четко выделить три основных периода в развитии:
1-й период 
– начало развития, «молодость».
2-й период 
– интенсивное развитие, «зрелость».
3-й период 
– экстенсивное развитие, «старость».
Зная, на каком из участков развития находится система в момент наблюдения, можно использовать упрощенные, приближенные формулы, описывающие развитие системы. Так, при малых t развитие может быть описано экспоненциальной функцией
(2.4)
при больших t в момент «старости»
(2.5)
то есть система асимптотически приближается к максимуму.
Полученную экспериментально логистическую функцию можно использовать для вскрытия внутренней структуры системы путем выяснения механизма развития. Такой качественный переход к совершенствованию анализа системы может быть осуществлен путем перехода к дифференциальному описанию системы (феноменологии). Зная уравнение (2.1) логистической функции, можно составить дифференциальное уравнение, порождающее эту функцию в качестве решения. Для этого продифференцируем (2.1) по времени, после чего получим
(2.6)
где 
.
Уравнение (2.6) позволяет наглядно вскрыть структуру развивающейся системы (популяции). Действительно, динамика изменения общей численности популяции определяется двумя процессами – рождением и гибелью. Вводя обобщенные показатели рождаемости (B) и смертности (L), можно (2.6), исходя из закона сохранения численности популяций, записать в виде
(2.7)
где 
Таким образом, закон логистического роста отражает такую структуру биологической популяции, когда при постоянной рождаемости наблюдается линейный рост смертности, пропорциональный существующей численности. Физически это нелинейный рост, так как он описывается нелинейным дифференциальным уравнением (2.6) и определяется многими лимитирующими факторами.
Как будет показано далее, практически все процессы роста в развивающихся системах любой природы нелинейные, что на определенных этапах развития может приводить к качественным скачкам.
Дальнейшие исследования роста и развития биологических популяций показали универсальность логистических функций, описывающих динамику развития самых разнообразных популяций.
Развитие математической биологии привело к необходимости изучения взаимодействия системы биологических популяций – биологических сообществ, характеризующих окружающую среду – экологическую систему. Общая математическая модель экологической системы, состоящая из множества взаимодействующих популяций, может быть представлена системой нелинейных дифференциальных уравнений [4, 7]:
(2.8)
где 
Здесь коэффициенты 
приобретают реальный физический смысл, то есть 
может быть отождествлен с внутривидовой конкуренцией, а 
– с межвидовой конкуренцией популяций. Если рассматривать произвольный вид нелинейной функции 
, то уравнения (2.8) носят общий характер, описывая развивающиеся системы самой различной природы. Эти уравнения получили название эволюционных.