Суммативное оценивание за раздел
«Неравенства»
Тема Квадратное неравенство
Рациональное неравенство
Решение систем неравенств
Цель обучения 8.2.2.8 решать квадратные неравенства
8.2.2.9 решать рациональные неравенства
8.2.2.10 решать системы из двух неравенств, одно из которых линейное, а второе-квадратное
Критерий оценивания Обучающийся
· Решает квадратные неравенства
· Решает рациональные неравенства
· решает системы из двух неравенств, одно из которых линейное, а второе-квадратное
Время выполнения 25 минут
1 вариант
1.Для каждого неравенства укажите множество его решений(показать решение каждого неравенства, затем выбрать нужный ответ и заполнить таблицу ответов)
А) х2 + 4 > 0. Б) x2 – 4 > 0. В) x2 – 4 < 0. Г) х2 + 4 < 0
1) (- ∞; -2)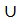 
(2; + ∞). 2) (- ∞; + ∞). 3) (-2; 2). 4) (2; + ∞) 5) 
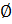6) (- ∞; -2)
| А | Б | В | Г | |
| ответ |
[5]
2. Решите неравенство:. (4-х)(3х-1)(х+8) ≤ 0
[5]
3. Решите систему неравенств:
2х2+5х+2≥0,
3х+9<0.
[5]
| Критерий оценивания | № задания | Дескриптор | Балл |
| Обучающийся | |||
| Решает квадратные неравенства | Определяет соответствующий вывод для неравенства, решением которого является вся числовая прямая | ||
| Определяет соответствующий вывод для неравенства, которое не имеет решений | |||
| Определяет соответствующий вывод для неравенства, решением которого является промежуток | |||
| Определяет соответствующий вывод для неравенства, решением которого является объединение двух промежутков | |||
| Обосновывает свои выводы | |||
| Решает рациональные неравенства | Представляет каждый двучлен в виде (х-х1) | ||
| Делит неравенство на -1 | |||
| Отмечает нули на координатной прямой | |||
| Определяет знаки произведения в каждом промежутке | |||
| Записывает ответ | |||
| Решает системы из двух неравенств, одно из которых линейное, а второе-квадратное | Определяет метод решения первого неравенства | ||
| Решает первое неравенство | |||
| Решает второе неравенство | |||
| Изображает решения на числовой оси | |||
| Записывает ответ | |||
| Всего баллов |
Суммативное оценивание за раздел
«Неравенства»
Тема Квадратное неравенство
Рациональное неравенство
Решение систем неравенств
Цель обучения 8.2.2.8 решать квадратные неравенства
8.2.2.9 решать рациональные неравенства
8.2.2.10 решать системы из двух неравенств, одно из которых линейное, а второе-квадратное
Критерий оценивания Обучающийся
· Решает квадратные неравенства
· Решает рациональные неравенства
· решает системы из двух неравенств, одно из которых линейное, а второе-квадратное
Время выполнения 25 минут
2 вариант
.Для каждого неравенства укажите множество его решений(показать решение каждого неравенства, затем выбрать нужный ответ и заполнить таблицу ответов)
А) 9– х2 > 0. Б) 9+ x2 > 0. В) 9– x2 < 0. Г) 9+ х2 < 0
1) (- ∞; -3) 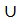(3; + ∞). 2) (- ∞; + ∞). 3) (-3; 3). 4) (3; + ∞) 5) 6) (- ∞; -3)
| А | Б | В | Г | |
| ответ |
[5]
2. Решите неравенство:. (9-х)(6х+1)(х-7) ≥ 0
[5]
3. Решите систему неравенств:
х2+7х+6˃0,
2х-6≤0.
[5]
| Критерий оценивания | № задания | Дескриптор | Балл |
| Обучающийся | |||
| Решает квадратные неравенства | Определяет соответствующий вывод для неравенства, решением которого является вся числовая прямая | ||
| Определяет соответствующий вывод для неравенства, которое не имеет решений | |||
| Определяет соответствующий вывод для неравенства, решением которого является промежуток | |||
| Определяет соответствующий вывод для неравенства, решением которого является объединение двух промежутков | |||
| Обосновывает свои выводы | |||
| Решает рациональные неравенства | Представляет каждый двучлен в виде (х-х1) | ||
| Делит неравенство на -1 | |||
| Отмечает нули на координатной прямой | |||
| Определяет знаки произведения в каждом промежутке | |||
| Записывает ответ | |||
| Решает системы из двух неравенств, одно из которых линейное, а второе-квадратное | Определяет метод решения первого неравенства | ||
| Решает первое неравенство | |||
| Решает второе неравенство | |||
| Изображает решения на числовой оси | |||
| Записывает ответ | |||
| Всего баллов |