Метод Гаусса
Данный метод является универсальным методом решения систем линейных алгебраических уравнений, так как с помощью него можно найти решения как определенных, так и неопределенных систем.
Суть метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы. Для этого используются элементарные преобразования матриц:
- умножение (деление) всех элементов какой-либо строки расширенной матрицы системы на постоянное число, не равное нулю,
- сложение (вычитание) каких-либо двух строк расширенной матрицы системы,
- перестановка строк расширенной матрицы системы.
При этом расширенная матрица системы приводится к ступенчатому виду, после чего вычисляются по очереди значения неизвестных системы.
Рассмотрим несколько примеров решения систем линейных алгебраических уравнений методом Гаусса.
4.
Сущность метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы. Сначала из первого уравнения выражаем  и подставляем во все остальные уравнения. После этого из полученного второго уравнения выражаем
и подставляем во все остальные уравнения. После этого из полученного второго уравнения выражаем 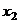 и подставляем во все следующие уравнения и так далее.
и подставляем во все следующие уравнения и так далее.
Все преобразования такого рода удобно выполнять, воспользовавшись так называемой расширенной матрицей системы:

 .
.
Матрица, расположенная слева от вертикальной черты, называется основной, а вся матрица расширенной (здесь справа от черты стоят элементы правой части системы). Элементарные преобразования уравнений системы равносильны эквивалентным преобразованиями строк расширенной матрицы системы:
1. Можно поменять местами любые две строки матрицы  .
.
2. Любую строку матрицы  можно умножить на любое отличное от нуля число.
можно умножить на любое отличное от нуля число.
3. Любую сроку матрицы  можно прибавить к любой другой строке.
можно прибавить к любой другой строке.
Чаще всего преобразования 2 и 3 заменяют следующим:
Любую строку расширенной матрицы системы можно умножить на некоторое число и прибавить к любой другой строке.
Метод Гаусса (метод последовательного исключения переменных) при использовании расширенной матрицы системы сводится к получению нулей ниже главной диагонали данной матрицы с помощью эквивалентных преобразований, чаще всего с помощью преобразования 4.
Если в результате элементарных преобразований в расширенной матрице системы, до черты (т.е. в основной матрице) получается матрица треугольного вида, т.е. все элементы ниже главной диагонали равны нулю, а диагональные элементы все ненулевые:

 ,
,
то рассматриваемая система совместная и определённая, т.е. имеет единственное решение.
 Если после преобразований, в какой - либо строке матрицы получили до черты все нулевые элементы, а элемент, стоящий в той же строке после черты - ненулевой, например
Если после преобразований, в какой - либо строке матрицы получили до черты все нулевые элементы, а элемент, стоящий в той же строке после черты - ненулевой, например

где  , то рассматриваемая система несовместна, т.е. не имеет решений.
, то рассматриваемая система несовместна, т.е. не имеет решений.
Если же после преобразования расширенной матрицы, после получения нулей ниже главной диагонали в нижней строке основной матрицы осталось больше одного ненулевого элемента, т.е. основная матрица имеет вид трапеции, например

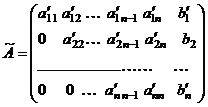 ,
,
то система имеет бесконечно много решений.
Пример 9.
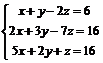 .
.
Составим расширенную матрицу системы и приведем ее к ступенчатому виду.

 . Умножим элементы первой строки сначала на -2 и сложим с соответствующими элементами второй строки, а затем на –5 и сложим с соответствующими элементами третьей строки.
. Умножим элементы первой строки сначала на -2 и сложим с соответствующими элементами второй строки, а затем на –5 и сложим с соответствующими элементами третьей строки. 
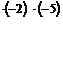 ~
~  . Теперь умножим элементы второй строки на 3 и сложим с соответствующими элементами третьей строки.
. Теперь умножим элементы второй строки на 3 и сложим с соответствующими элементами третьей строки.



 ~
~  . Получили матрицу ступенчатого вида. Теперь составим систему уравнений, соответствующую этой матрице.
. Получили матрицу ступенчатого вида. Теперь составим систему уравнений, соответствующую этой матрице.
 . Из третьего уравнения находим
. Из третьего уравнения находим  , подставляем во второе уравнение и находим
, подставляем во второе уравнение и находим  , подставляем в первое уравнение и находим
, подставляем в первое уравнение и находим 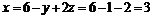 .
.
Ответ:  .
.
«Ступеньки» можно получить и в другом направлении.
Пример 10.
 .
.
Составим расширенную матрицу системы и приведем ее к ступенчатому виду.



 ~
~ 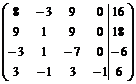
 ~
~
 ~
~  ~
~ 
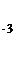 ~
~
 |
~  . Получили матрицу ступенчатого вида.
. Получили матрицу ступенчатого вида.
Теперь составим систему уравнений, соответствующую этой матрице.
 . Из первого уравнения находим
. Из первого уравнения находим 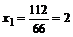 ,, подставляем во второе уравнение и находим
,, подставляем во второе уравнение и находим  , подставляем в третье уравнение и находим
, подставляем в третье уравнение и находим  , подставляем в четвертое уравнение и находим
, подставляем в четвертое уравнение и находим 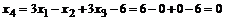 .
.
Ответ:  .
.
Пример 11.
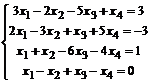 .
.
Составим расширенную матрицу системы и приведем ее к ступенчатому виду.

 ~
~  .
.
Поменяем местами первую и третью строки матрицы.
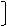


 ~
~ 
 ~
~ 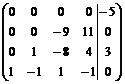 . Получили ступенчатую матрицу.
. Получили ступенчатую матрицу.
Ей соответствует система 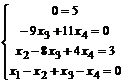 . Так как первое равенство системы ложное, то данная система не имеет решений, то есть является несовместной.
. Так как первое равенство системы ложное, то данная система не имеет решений, то есть является несовместной.
Ответ: нет решений.
Пример 12.
 . Особенностью данной системы является то, что в ней уравнений больше, чем неизвестных.
. Особенностью данной системы является то, что в ней уравнений больше, чем неизвестных.
Составим расширенную матрицу системы и приведем ее к ступенчатому виду.


 ~
~ 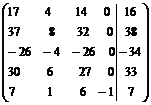
 ~
~
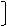

 ~
~ 


 ~
~  .
.
Первые три строки соответствуют одному и тому же уравнению системы, поэтому из них можно оставить только одну.
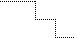
 . Эта матрица уже имеет ступенчатый вид, причем строк в ней меньше, чем столбцов. Следовательно, система, соответствующая полученной матрице, является неопределенной, то есть имеет бесконечное множество решений.
. Эта матрица уже имеет ступенчатый вид, причем строк в ней меньше, чем столбцов. Следовательно, система, соответствующая полученной матрице, является неопределенной, то есть имеет бесконечное множество решений.
 ,
,  – свободная переменная,
– свободная переменная,  ,
,  ,
,  – базисные переменные. Выразим базисные переменные через свободные.
– базисные переменные. Выразим базисные переменные через свободные.
Из первого уравнения выражаем  , подставляем во второе уравнение и выражаем
, подставляем во второе уравнение и выражаем 
=  , подставляем в третье уравнение и находим
, подставляем в третье уравнение и находим 
 . Так как
. Так как  – свободная переменная, то она может принимать любое значение, пусть
– свободная переменная, то она может принимать любое значение, пусть  =с, тогда
=с, тогда 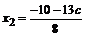 ,
,  =
= 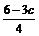 ,
, 

Общее решение: (с; 
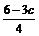 ;
;  ), где с – любое действительное число.
), где с – любое действительное число.
Для проверки можно найти какое-либо частное решение, придав конкретное значение независимой переменной.
Пусть с=6, тогда частное решение можно вычислить, подставив это значение в общее решение.
(6; 
 ;
;  )=
)=  – частное решение. Подставим его во все уравнения первоначальной системы.
– частное решение. Подставим его во все уравнения первоначальной системы.
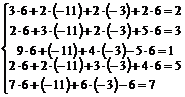

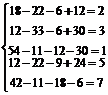

 .
.
Получившиеся числовые равенства свидетельствуют о том, что система решена верно.
Ответ: (с; 
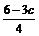 ;
;  ), где с – любое действительное число.
), где с – любое действительное число.
Пример 13.
 . Особенность данной системы в том, что в ней неизвестных больше, чем уравнений. Составим расширенную матрицу системы и приведем ее к ступенчатому виду.
. Особенность данной системы в том, что в ней неизвестных больше, чем уравнений. Составим расширенную матрицу системы и приведем ее к ступенчатому виду.
 . Для удобства поменяем местами первую и вторую строки матрицы.
. Для удобства поменяем местами первую и вторую строки матрицы.



 ~
~ 

 ~
~
~  . Из двух одинаковых последних строк оставляем одну, а другую отбрасываем.
. Из двух одинаковых последних строк оставляем одну, а другую отбрасываем.

 . Получили ступенчатую матрицу, в которой строк меньше, чем неизвестных. Следовательно, система, соответствующая этой матрице, является неопределенной, то есть имеет бесконечное множество решений.
. Получили ступенчатую матрицу, в которой строк меньше, чем неизвестных. Следовательно, система, соответствующая этой матрице, является неопределенной, то есть имеет бесконечное множество решений.
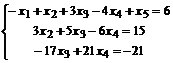 . Пусть
. Пусть  ,
,  ,
,  – базисные переменные, а
– базисные переменные, а  и
и  - свободные переменные. Выразим базисные переменные через свободные.
- свободные переменные. Выразим базисные переменные через свободные.
Из третьего уравнения выражаем  , подставляем во второе уравнение и выражаем
, подставляем во второе уравнение и выражаем 
= 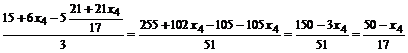 , подставляем в первое уравнение и находим
, подставляем в первое уравнение и находим 
 . Так как
. Так как  и
и  - свободные переменные, то они могут принимать любые значения, пусть
- свободные переменные, то они могут принимать любые значения, пусть  , а
, а  , тогда
, тогда  ,
, 
 ,
, 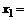

Общее решение: ( ;
; 
 ;
; 
 ), где
), где  и
и  – любые действительные числа.
– любые действительные числа.
Для проверки можно найти какое-либо частное решение, придав конкретное значение независимым переменным.
Пусть  =-1,а
=-1,а  =1, тогда частное решение можно вычислить, подставив эти значения в общее решение.
=1, тогда частное решение можно вычислить, подставив эти значения в общее решение.
(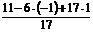 ;
; 
 ;
; 
 )=
)=  – частное решение. Подставим его во все уравнения первоначально заданной системы.
– частное решение. Подставим его во все уравнения первоначально заданной системы.




 .
.
Получившиеся числовые равенства свидетельствуют о том, что система решена верно.
Ответ: (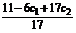 ;
; 
 ;
; 
 ), где
), где  и
и  – любые действительные числа.
– любые действительные числа.
Решая методом Гаусса однородные системы линейных алгебраических уравнений (системы, в которых свободные члены всех уравнений равны 0), которые всегда совместны, можно получить единственное – тривиальное решение (когда все значения неизвестных системы равны 0), если эта система определенная. Но можно получить и общее решение, если эта система неопределенная, выражающее закономерность, по которой получается бесконечное множество решений такой системы. В однородных неопределенных системах общее решение можно выразить в виде линейной комбинации частных решений, образующих фундаментальную систему линейно-независимых решений.
Пример 14.
 .
.
Решая методом Гаусса однородные системы, можно преобразовывать только основную матрицу, так как столбец свободных членов всегда будет нулевой.
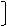
 ~
~  , если разделить все элементы четвертой строки на 2, то мы получим в матрице три одинаковых строки, из которых можно оставить одну, а остальные отбросить.
, если разделить все элементы четвертой строки на 2, то мы получим в матрице три одинаковых строки, из которых можно оставить одну, а остальные отбросить.

 . Получили ступенчатую матрицу, которой соответствует следующая однородная система:
. Получили ступенчатую матрицу, которой соответствует следующая однородная система:
 . Пусть
. Пусть  и
и  - базисные переменные, а
- базисные переменные, а  ,
,  и
и  - свободные переменные. Из второго уравнения системы выражаем
- свободные переменные. Из второго уравнения системы выражаем  =
= 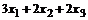 , подставляем в первое и выражаем
, подставляем в первое и выражаем  =
= 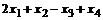 =
= 
 .
.
Так как у нас три свободных переменных, то фундаментальная система решений будет состоять из трех линейно независимых ненулевых частных решений.
Пусть  =1,
=1,  =0,
=0,  =0, тогда
=0, тогда  =3,
=3,  =5.
=5.  .
.
Пусть  =0,
=0,  =1,
=1,  =0, тогда
=0, тогда  =2,
=2,  =3.
=3.  .
.
Пусть  =0,
=0,  =0,
=0,  =1, тогда
=1, тогда  =2,
=2,  =1.
=1. 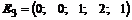 .
.
Решения 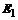 ,
,  и
и  образуют фундаментальную систему решений. Общее решение есть линейная комбинация решений
образуют фундаментальную систему решений. Общее решение есть линейная комбинация решений 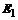 ,
,  и
и  .
.
Если  - общее решение данной системы, то
- общее решение данной системы, то  =
=  , где
, где  - любые действительные числа.
- любые действительные числа.
 =
=  , где
, где  - любые действительные числа.
- любые действительные числа.
Сделаем проверку.
Пусть  =2,
=2, 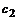 =-3,
=-3,  =4, тогда:
=4, тогда:
 =
= 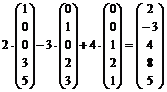 . Подставим полученные значения неизвестных в первоначально заданную систему.
. Подставим полученные значения неизвестных в первоначально заданную систему.


 . Система решена верно.
. Система решена верно.
Ответ:  =
=  , где
, где 
 .
.
Пример 15.
 .
.





 ~
~  ~
~ 
 ~
~  .
.
Однородная система, соответствующая полученной ступенчатой матрице, будет иметь столько же уравнений, сколько неизвестных. Такая система является определенной, следовательно, единственное ее решение имеет вид:  .
.
Рассмотрим пример решения системы методом Гаусса. Пусть дана система:

Составим расширенную матрицу этой системы:

 ˜
˜
Поменяем местами первую и третью строки матрицы:
 ˜
˜  ˜
˜
С помощью первой строки полученной матрицы получим нули в первом столбце. Для этого первую строку умножим на (-1) и прибавим к второй строке, и её же умножим на (-2) и прибавим к третьей строке, Получим новую матрицу
 ˜
˜  ˜
˜
Умножим третью строку на (-3) и прибавим ко второй строке и эту же строку прибавим к первой строке, получим
 ˜
˜  ˜
˜

 Вторую строку умножим на (2) и прибавим к третьей
Вторую строку умножим на (2) и прибавим к третьей
˜  ˜
˜  ˜
˜
Мы разделили последнюю строку на 47. После это третью строку умножим на (-29) и прибавим ко второй строке и ту же строку умножим на (6) и прибавим к первой строке:
 ˜
˜ 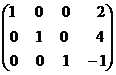 .
.
Слева от черты получили единичную матрицу, тогда после черты получено решение данной системы. Таким образом,  Сделаем проверку:
Сделаем проверку:

Получили тождественные равенства. Следовательно, в самом деле, получено решение системы.
Рассмотрим ещё один пример:

 Расширенная матрица этой системы имеет вид:
Расширенная матрица этой системы имеет вид:
 ˜
˜
Умножим первую строку на (-2) и прибавим к второй и третьей строке, эту же строку умножим на (-1) и прибавим к четвёртой строке, получим:
 ˜
˜  ˜
˜
Вторую строку умножим на (-1) и прибавим к первой строке и вторую строку просто прибавим к третьей строке:
 ˜
˜ 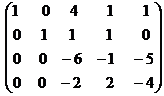 ˜
˜
Четвёртую строку разделим на (-2) и поменяем с третьей строкой:
 ˜
˜  ˜
˜
После этого получим нули в третьем столбце, для чего третью строку умножим на (-4) и прибавим к первой строке; умножим на (-1) и прибавим к второй строке; умножим на (6) и прибавим к третьей строке. Получим:

 ˜
˜  ˜
˜ 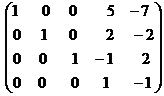 ˜
˜
Мы разделили последнюю строку на (-7). После этого можем получить нули в четвёртом столбце. Для этого последнюю строку прибавим к третьей строке; умножим на (-2) и прибавим к второй строке и, умножив на (-5), прибавим к первой строке. В результате получается матрица:
 ˜
˜  .
.
Слева, до черты, получили единичную матрицу. Тогда после черты находится решение, т.е.
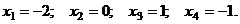
Подставив эти значения переменных в равенства системы, получим тождественные равенства.
Прежде чем перейти к рассмотрению систем произвольной размерности, вернёмся снова к понятию ранга матрицы, введённому в § 3. Приведём утверждение, доказывать которое мы не будем.
Утверждение. Ранг матрицы равен числу ненулевых строк в матрице, полученной в результате эквивалентных преобразований после получения нулей ниже главной диагонали матрицы.
Примеры. Найти ранги следующих матриц:
1.  ˜
˜
Получим нули в первом столбце. Для этого умножим первую строку на (-1) и прибавим к второй строке; умножим ту же строку на (-5) и прибавим к третьей строке и, аналогично, умножим её на (-7) и прибавим к четвёртой строке. Получим:
˜  ˜
˜
Умножим вторую строку на (-2) и прибавим соответственно к третьей и четвёртой
˜  ˜
˜  .
.
Следовательно ранг этой матрицы  .
.
2.  ˜
˜
С помощью первой строки получим нули в первом столбце. Для этого умножим её на (-2) и прибавим к второй строке, умножим на (-3) и прибавим к третьей и пятой строке, умно- жим на (-1) и прибавим к четвёртой строке. В результате получим:
˜ 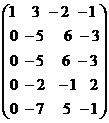 ˜
˜
Вторую строку умножим на (-1) и прибавим к третьей, четвёртую строку умножим на (-4) и прибавим к пятой:
˜  ˜
˜
Пятую строку умножим на (5) и прибавим к второй и умножим на (2) и прибавим к четвёртой:
˜  ˜
˜
четвёртую строку умножим на (-3) и прибавим к второй:
˜  ˜
˜  .
.
Ранг этой матрицы тоже равен  .
.
При исследовании систем важную ролю играет следующая теорема:
ТЕОРЕМА (Кронекера – Капелли). Ранг основной матрицы системы не превосходит ранга расширенной матрицы, т.е.
 , причём, если
, причём, если 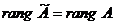 , то система совместна, а если
, то система совместна, а если  , то система несовместна (не имеет решений).
, то система несовместна (не имеет решений).
Рассмотрим пример.

 Тогда
Тогда  ˜
˜
Умножим первую строку на (-2) и прибавим к второй и третьей строке; после этого поменяем местами первую и вторую строки:
 |  | ||
˜  ˜
˜  ˜
˜
прибавим ко второй, а после этого прибавим к третьей:
 ˜
˜  ˜
˜
После этого прибавим вторую строку к третьей и получим матрицу:
 ˜
˜  .
.
В результате получили матрицу, у которой 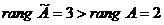 , следовательно, система несовместна. Решений нет.
, следовательно, система несовместна. Решений нет.
Если 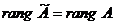 , т. е, если система совместна, то в случае, если
, т. е, если система совместна, то в случае, если 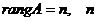 - число неизвестных, система имеет единственное решение. Если же
- число неизвестных, система имеет единственное решение. Если же  , то система имеет бесконечно много решений, при этом число свободных переменных (т.е. переменных, через которые можно выразить все остальные и которые могут принимать любые значения из множества действительных чисел)
, то система имеет бесконечно много решений, при этом число свободных переменных (т.е. переменных, через которые можно выразить все остальные и которые могут принимать любые значения из множества действительных чисел)  , а число базисных переменных (т.е. таких переменных, которые выражаем через свободные) равно
, а число базисных переменных (т.е. таких переменных, которые выражаем через свободные) равно  .
.
Рассмотрим примеры: решить системы уравнений методом Гаусса; найти общие и частные решения; сделать проверку.
1. 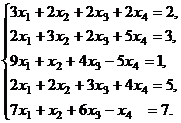
Запишем расширенную матрицу данной системы:


 ˜
˜
Уменьшим элементы первого столбца с помощью четвёртой строки. Для этого умножим её на (-1) и прибавим к первой и второй строке; умножим на (-4) и прибавим к третьей строке и, наконец, умножим на (-3) и прибавим к пятой строке.

 ˜
˜  ˜
˜
Теперь получим нули в первом столбце. Умножим первую строку на (-1) и прибавим к третьей и пятой строке; умножим её же на (-2) и прибавим к четвёртой строке. Получим:

 ˜
˜  ˜
˜
С помощью второй строки получим нули во втором столбце. Для этого умножим её на (7) и прибавим к третьей строке; умножим на (-2) и прибавим к четвёртой строке; умножим на (5) и прибавим к пятой строке:

 ˜
˜ 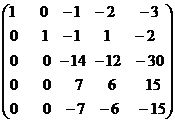 ˜
˜
Четвёртую строку умножим на (2) и прибавим к третьей строке и её же просто прибавим к пятой строке:
 ˜
˜  .
.
Видим, что в данном случае  , поэтому система совместна, но так как переменных 4, а ранг матрицы равен 3, то одна переменная свободная, а три базисных. За – пишем полученную систему:
, поэтому система совместна, но так как переменных 4, а ранг матрицы равен 3, то одна переменная свободная, а три базисных. За – пишем полученную систему:

Выберем свободную переменную  , тогда из третьего уравнения
, тогда из третьего уравнения  ; из второго уравнения
; из второго уравнения

из первого уравнения

Таким образом, общее решение системы имеет вид:
 ,
,
т.е. при любом значении  мы будем получать решения системы. Это общее решение. Задавая какие – либо значения постоянной
мы будем получать решения системы. Это общее решение. Задавая какие – либо значения постоянной  , будем получать частные решения. Например, при
, будем получать частные решения. Например, при  получаем частное решение
получаем частное решение

Сделаем проверку:

Получили тождественные равенства. Аналогично можно получать другие частные решения и делать проверку. Например, при  :
:  . Подставив эти значения в уравнения системы, снова получим тождественные равенства. Таким же образом, при разных значениях
. Подставив эти значения в уравнения системы, снова получим тождественные равенства. Таким же образом, при разных значениях  можем получить любое частное решение системы.
можем получить любое частное решение системы.
Ещё одна система:
2. 
Её расширенная матрица имеет вид:

 ˜
˜
Поменяем местами первую и вторую строки:

 ˜
˜  ˜
˜
С помощью первой строки получим нули в первом столбце. Для этого умножим её на (-3) и прибавим к второй строке; умножим на (-4) и прибавим к третьей строке; умножим на
(-2) и прибавим к четвёртой строке, получим:

 ˜
˜  ˜
˜
 Вторую строку умножим на (-1) и прибавим к третьей и четвёртой, получим
Вторую строку умножим на (-1) и прибавим к третьей и четвёртой, получим
˜  .
.
Видим, что ранг полученной матрицы равен
 .
.
Поэтому система совместна. Число базисных переменных равно рангу матрицы, т.е. две базисные переменные Число свободных переменных равно разнице «число переменных» = 5 минус «ранг матрицы» = 2, т. е 3 свободные переменные.
Запишем полученную систему:

В качестве базисных переменных, если есть возможность, удобно выбрать переменные с единичными коэффициентами, чтобы избежать вычислений с дробными выражениями. Например, в данном примере, в качестве базисных можем выбрать  , а остальные считать свободными, т.е. положим:
, а остальные считать свободными, т.е. положим:

Тогда из второго уравнения:
 ,
,
а из первого уравнения:
 .
.
Следовательно, общее решение имеет вид:


Запишем частное решение и сделаем проверку. Например, при  получим:
получим:


Сделаем проверку:


Получили тождественное равенство. Аналогичным образом можно получить любое другое частное решение, например, при  получим:
получим:

Подставив эти значения переменных в уравнения системы, также получим верные равенства.
ОДНОРОДНЫЕ СИСТЕМЫЛИНЕЙНЫХ УРАВНЕНИЙ.
Отдельно следует выделить множество однородных уравнений, т.е. уравнений вида:

Такие системы всегда совместны, так как всегда имеется тривиальное (т.е. нулевое решение 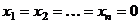 ).
).
Нулевое решение будет единственным, если ранг основной матрицы системы равен числу неизвестных, т.е. в случае  . Если же
. Если же  , то система имеет бесконечно много решений.
, то система имеет бесконечно много решений.
Рассмотрим примеры: найти фундаментальные системы решений однородных систем линейных уравнений
1. 
Для однородных систем нет смысла писать расширенную матрицу, так как элементарные преобразования не меняют нули, стоящие в правых частях системы уравнений. Поэтому про -изводим преобразования основной матрицы системы: