Определение. Квадратной называется матрица, у которой число строк равно числу столбцов, т.е. матрица вида
.
Квадратную матрицу размерности n на n называют матрицей n -го порядка.
Вектор 
называют главной диагональю квадратной матрицы, а вектор 
– побочной диагональю.
Виды квадратных матриц:
· треугольная матрица – квадратная матрица, у которой элементы ниже (выше) главной диагонали нулевые;
· диагональная матрица – квадратная матрица, у которой все элементы вне главной диагонали нулевые;
· скалярная матрица – квадратная матрица, у которой все элементы главной диагонали равны, а все остальные элементы нулевые;
· единичная матрица – квадратная матрица, у которой все элементы главной диагонали равны единицы, а все остальные элементы нулевые.
Перечисленные виды квадратных матриц обладают рядом свойств. Особое место среди них занимает единичная матрица. Исключительность матриц такого вида выражена в следующем свойстве.
Теорема 1. 
Доказательство. Покажем, что 
. Две матрицы равны, если их размерности совпадают и равны их элементы соответственно.
По определению умножения матриц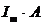 
– матрица размерности m на n – как и матрица A. Рассмотрим произвольный элемент матрицы 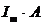и покажем, что он совпадет с соответствующим элементом матрицы A:
Тождество 
докажите самостоятельно■
Следствие.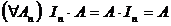 
.
Таким образом, единичная матрица n -го порядка играет роль единицы на множестве квадратных матриц n -го порядка.
Определение. Квадратная матрица A n –го порядка называется обратимой, если существует матрица B n –го порядка такая, что 
. Сама матрица B при этом называется обратной для матрицы A и обозначается 
.
Очевидно, что единичная матрица обратима, а обратной для единичной матрицы является сама эта матрица.
Лемма (свойства обратимых матриц). Если матрицы A и B обратимы, то:
1) 
; 2) 
; 3) 
.
Доказательство. Первое очевидно.
Покажем, что матрица 
является обратной для 
. Действительно, 
. 
.
Самостоятельно покажите, что 
является обратной для матрицы 
■
Теорема 2. (критерий обратимости матрицы) Квадратная матрица обратима тогда и только тогда, когда ее ранг равен ее порядку.
Доказательство.
Необходимость. Пусть матрица A n -го порядка обратима. Покажем, что 
. Так как матрица A обратима, то существует матрица B такая, что . Но тогда по лемме о строчечном пространстве произведения матриц имеем 
. В то же время 
, так как строки единичной матрицы – стандартный базис пространства 
. Получаем, 
, откуда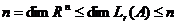 
. Итак, 
, а 
, т.е. .
Достаточность. Пусть A – матрица n -го порядка и . Покажем, что она обратима.
По определению 
, поэтому базис строчечного пространства матрицы A состоит из n строк матрицы A n -го порядка, а значит все строки матрицы линейно независимы. Поскольку их количество совпадает с размерностью , то строки матрицы A образуют базис пространства и через них выражается всякий вектор этого пространства, в том числе и строки матрицы I. По следствию из леммы о строчечном пространстве произведения матриц, найдется матрица B такая, то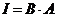 
.
По определению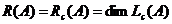 
, поэтому базис столбцового пространства матрицы A состоит из n столбцов матрицы A n -го порядка, а значит все столбцы матрицы линейно независимы. Поскольку их количество совпадает с размерностью , то столбцы матрицы A образуют базис пространства и через них выражается всякий вектор этого пространства, в том числе и столбцы матрицы I. По следствию из леммы о столбцовом пространстве произведения матриц, найдется матрица C такая, то 
.
Осталось показать, что 
. Действительно, 
■
Замечание. Квадратную матрицу, у которой ранг совпадет с ее порядком, называют невырожденной.