Перенос теплоты от одного тела к другому, температура которого ниже на бесконечно малую величину, представляет собой обратимый процесс, т.к. направление переноса можно изменить на противоположное, для этого нужно изменить Т одного из тел на бесконечно малую величину.
Примеры:
Плавление вещества в точке Тпл и испарение жидкости при постоянном парциальном давлении, равном давлению его насыщенного пара – примеры изотермических превращений, которые могут идти в обратном направлении при бесконечно малом изменении температуры.
Для такого рода изменений можно рассчитать ∆S:
Пусть Т=const интегрируем уравнение 2.1 dS≡ 
/T
S2-S1=∆S =qобр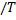 
(2.6)
Где qобр – теплота поглощенная при обратном изменении.
Для 1 моля при P,T=const
(2.7)
Поскольку количество теплоты, полученное системой равно количеству теплоты, отданному окружающей средой, изменение S для окружающей среды равно ∆S, а для системы с обратным знаком; суммарное изменение S для системы и окружающей среды равно нулю, если перенос теплоты происходит обратимо, согласно уравнению 2.4 (для изолированных систем).
Пусть газ находится в равновесии с твердым телом в (.) плавления. Тогда согласно представлению об S как о мере неупорядоченности S=f(Ω).
Мольная S пара всегда > чем S жидкости, а мольная S жидкости всегда > S твердого тела.
(ТД не рассматривает молекулы или конкретные модели систем, но для уяснения смысла ТД функций полезно перейти к молекулярным моделям вещества)
В статистической физике будут рассмотрена молекулярная модель вещества и приведены расчеты ТД величин по данным о строении молекул. Мы здесь вспомним только рассуждения Больцмана о возможном распределении молекул при взаимной диффузии двух идеальных кристаллов. Согласно Больцману, состояния смешанного кристалла более вероятно, чем состояние чистого вещества и именно это является причиной существования равновесных смесей.
S обладает свойством аддитивности => S системы, состоящей из двух частей есть сумма S=S1+S2.
Пусть число равновероятных распределений (т.е. микросостояний) для одной части системы Ω1 , для другой - Ω2. То для всей системы число равновероятных распределений есть Ω1* Ω2, так как любое распределение в одной части с любым распределением в другой части дает определенное микросостояние.
Пусть S=f(Ω), тогда S=S1+S2 и f(Ω1*Ω2)= f(Ω1)+ f(Ω2).
Чтобы эти соотношения выполнялись, Больцман постулировал
S=k*ln(Ω), где kБ=R/Na
(2.8)
Используя описанное выше представление о числе возможных микрораспределений в системе можно понять расширение идеального газа
Обратимое изменение Т
Возрастание S системы можно рассчитать, например, если оно вызвано увеличением T, т.к. изменение Т можно осуществить обратимо.
Пусть Р=const, тогда нагревание приводит к тому, что q, поглощенное на каждой бесконечно малой стадии равняется CpdT:
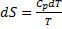
(2.9)
(2.9’)
Пусть Сp≠f(T) => S2-S1=Cp(lnT2-lnT1)=Cpln(T2/T1)=2/303Cplg(T2/T1)
Тот факт, что всегда S больше при более высокой Т согласуется с большей неупорядоченностью движения молекул при более высокой температуре.
Пусть теперь Т и Р изменяются обратимо, тогда для 1 моля идеального газа (I закон ТД) dU=dq-PdV
Идеальный газ=> 
Бесконечно малое изменение S в расчёте на 1 моль
Пусть СV≠f(T,V)
После интегрирования.
(2.10)
Это уравнение применимо к любому изменению состояния идеального газа.
Пусть Т=const (процесс испарения, плавления), тогда
(2.11)
Отсюда следует:
Для увеличения объема идеального газа в 10 раз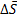 
=(1,987)*2.303=4.59 Кал/(К*моль).
S идеального газа изменяется на эту величину как при обратимом, там и при необратимом изотермическом расширении, т.к. 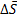зависит от значений S в начальном и конечном состоянии.