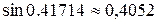Вычисление значений функций
При компьютерных вычислениях значений функций, заданных формулами, далеко не безразлично, в каком виде записана соответствующая формула. Математически эквивалентные выражения часто оказываются неравноценными с точки зрения практики вычислений. Рассмотрим приемы, сводящие вычисление некоторых функций к циклам из элементарных операций.
2.1. Вычисление значения многочлена по схеме Горнера
Пусть дан многочлен 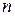 -й степени с действительными коэффициентами
-й степени с действительными коэффициентами
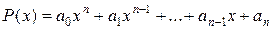 ,
,
где 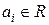 ,
,  .
.
Требуется найти значение 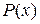 при
при 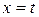 , т.е.
, т.е.
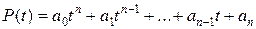 .
.
Если находить значения каждого члена и суммировать их, то при больших 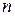 потребуется выполнить большое число операций (
потребуется выполнить большое число операций (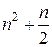 умножений и
умножений и 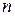 сложений). Кроме того, это может привести к потере точности за счет погрешностей округления.
сложений). Кроме того, это может привести к потере точности за счет погрешностей округления.
Схема Горнера – алгоритм вычисления значения многочлена, записанного в виде суммы одночленов, при заданном значении переменной.
Проиллюстрируем его идею на примере многочлена третьей степени:
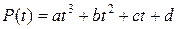 .
.
Его можно представить в виде
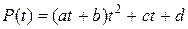
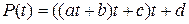 .
.
В общем случае
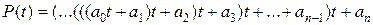 .
.
Обозначим:
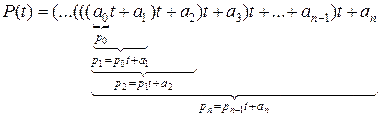
Отсюда, последовательно вычисляя числа
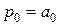
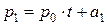
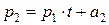 (1)
(1)
………………
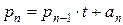 ,
,
находим 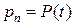 .
.
Таким образом, вычисление значения многочлена 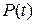 сводится к вычислению совокупности
сводится к вычислению совокупности
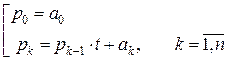 (2)
(2)
Вычисление значений многочлена 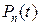 по схеме Горнера требует выполнения
по схеме Горнера требует выполнения 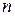 умножений и
умножений и 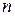 сложений. Во многих практических расчетах применение правила Горнера не только экономит машинное время, но и повышает точность за счет уменьшения верхнего предела ошибки округления.
сложений. Во многих практических расчетах применение правила Горнера не только экономит машинное время, но и повышает точность за счет уменьшения верхнего предела ошибки округления.
Вычисление значений рациональных дробей
Рациональной дробью называют отношение двух многочленов
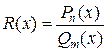 ,
,
где 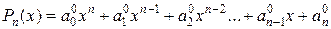 ,
,
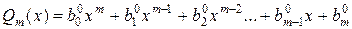 .
.
Рациональная дробь называется правильной, если n < m, т.е. если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе. В противном случае (если n ≥ m) дробь называется неправильной.
Пример. Указать, какие из приведённых ниже дробей являются рациональными. Если дробь является рациональной, то выяснить, правильная она или нет.
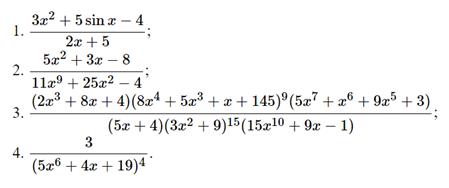
Пусть требуется вычислить значение 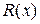 в точке
в точке 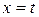 :
:
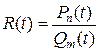 .
.
Числитель и знаменатель данной дроби можно найти, пользуясь схемой Горнера. Отсюда получаем простой способ вычисления числа 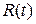
Вычисление значений показательной функции
Разложение функции в ряд Тейлора во многих случаях является удобным способом вычисления значений этой функции.
Для показательной функции 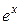 справедливо разложение
справедливо разложение
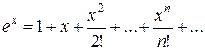 (
(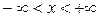 ). (1)
). (1)
Приближенное вычисление 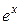 по формуле (1) для малых
по формуле (1) для малых 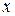 удобно производить по схеме
удобно производить по схеме
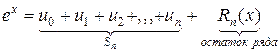 ,
,
где
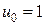 ,
,
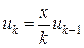 ,
, 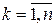 .
.
Пусть 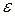 – заданная допустимая погрешность вычислений, тогда процесс суммирования следует прекратить, как только будет выполнено неравенство
– заданная допустимая погрешность вычислений, тогда процесс суммирования следует прекратить, как только будет выполнено неравенство
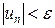 .
.
Пример. Найти 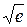 с точностью до
с точностью до 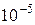 .
.
Пользуемся формулой
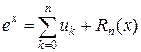 ,
,
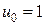 ,
,
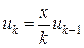 ,
, 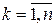 .
.
Слагаемые будем подсчитывать с двумя запасными десятичными знаками.
Последовательно имеем

Округляя сумму до пяти десятичных знаков после запятой, получим
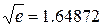 .
.
Вычисление значений синуса и косинуса
Для вычисления значений функций 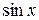 и
и 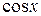 пользуемся степенными разложениями
пользуемся степенными разложениями
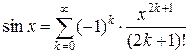 (
(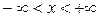 ) (1)
) (1)
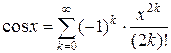 (
(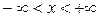 ) (2)
) (2)
Ряды (1) и (2) при больших 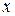 сходятся медленно, но, учитывая периодичность функций
сходятся медленно, но, учитывая периодичность функций 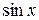 и
и 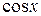 и формулы приведения тригонометрических функций, легко заключить, что достаточно уметь вычислять
и формулы приведения тригонометрических функций, легко заключить, что достаточно уметь вычислять 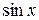 и
и 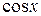 для промежутка
для промежутка
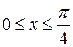 .
.
При этом используют следующие рекуррентные формулы
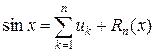 ,
,
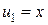 ,
,
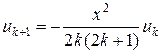 ,
, 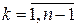
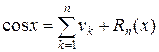 ,
,
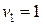 ,
,
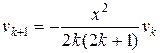 ,
, 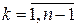
Т.к. в промежутке 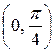 ряд знакочередующийся с монотонно убывающими по модулю членами, то для его остатка
ряд знакочередующийся с монотонно убывающими по модулю членами, то для его остатка 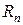 справедлива оценка
справедлива оценка
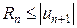 .
.
Аналогично для ряда (2)
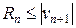 .
.
Следовательно, процесс вычисления 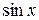 и
и 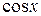 можно прекратить, как только очередной полученный член ряда по модулю будет меньше допустимой погрешности
можно прекратить, как только очередной полученный член ряда по модулю будет меньше допустимой погрешности 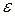 .
.
Пример. Вычислить 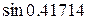 с точностью до
с точностью до 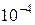
Получаем:
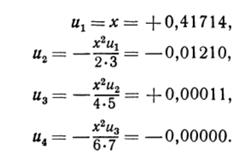
Сумма: 0,40515
Отсюда