Так как для наглядного представления декартова произведения двух числовых множеств можно использовать прямоугольную систему координат, то помимо задания, в котором требуется перечислить элементы декартова произведения двух множеств предложены ещё два типа задач. К первому типу относятся задачи, где нужно изобразить на координатной плоскости декартово произведение двух числовых множеств. Ко второму – задачи, в которых на координатной плоскости изображены фигуры, являющиеся графиком декартова произведения двух числовых множеств, и требуется указать данные множества.
Задача. Изобразите на координатной плоскости декартово произведение множеств X = {x | x Î N и x < 4} и Y = {y | y Î R и -1 < y < 3}.
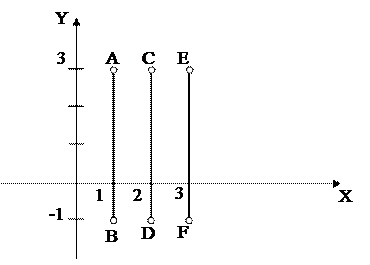Решение. В данном случае множество Х конечно, его элементы можно перечислить Х = {1, 2, 3}. Множество Y – бесконечное, его можно записать в виде числового промежутка Y = (-1; 3). Так как множество Y бесконечно, то перечислить все элементы декартова произведения множеств Х и Y невозможно, но можно представить процесс образования этого декартова произведения. Так как множество Х состоит из трех элементов, а множество Y содержит все действительные числа от -1 до 3, то декартово произведение Х ´ Y будет состоять из бесконечного множества пар, в каждой паре первая компонента либо 1, либо 2, либо 3, а вторая – любое действительное число из промежутка (-1; 3). Все пары, первая компонента которых есть число 1, а вторая пробегает значения из промежутка (-1; 3), точками отрезка АВ; пары, первая компонента которых есть число 2, а вторая принимает все значения из промежутка (-1; 3), – точками отрезка СD, а пары, первая компонента которых есть число 3, а вторая – любое действительное число из промежутка (-1; 3) – точками отрезка EF. Таким образом, декартово произведение множеств Х ´ Y на координатной плоскости изобразится тремя отрезками.
Рис. 2.
Задание 5. Понятие разбиения множества на класы
В данное задание включены два типа задач. В каждом варианте один тип. Решение задач первого типа, связанные с оценкой правильности разбиения множества на классы, основано на непосредственной проверке условий разбиения множества на классы. Для решения задач второго типа, связанные с самостоятельным разбиением множества на классы при использовании двух свойств, целесообразно воспользоваться кругами Эйлера и с их помощью изобразить исходное множество и те множества, характеристические свойства которых заданы в условии. Затем выделить непересекающиеся подмножества, объединение которых составляет исходное множество, и охарактеризовать их.
Задача 1. Учащийся А из множества четырехугольников выделил подмножества трапеций, параллелограммов и прямоугольников. Произошло ли разбиение множества на классы?
Решение. Разбиение множества на классы произойдет в том случае, если будут выполнены следующие условия:
1. Подмножества попарно не пересекаются.
2. При объединении всех подмножеств получается исходное множество.
В данном случае не выполняется первое условие. Действительно, множество прямоугольников является подмножеством параллелограммов, следовательно, эти множества пересекаются. Это значит, что разбиения множества четырехугольников на классы не произошло.
Задача 2. На какие классы разбивается множество натуральных чисел, если использовать такие свойства; «делиться на 2» и «быть однозначным»?
Решение. Обозначим через А множество четных натуральных чисел, а через В – множество однозначных чисел. Заметим, что А∩В≠Ø, так как некоторые четные числа являются однозначными, а некоторые однозначные числа – четными. Далее с помощью кругов Эйлера изобразим множества А. В и N и выделим классы разбиения. Из рисунка видим, что их 4. Охарактеризуем каждый из них:
I – множество четных однозначных натуральных чисел;
II – множество четных не однозначных натуральных чисел;
III – множество нечетных однозначных натуральных чисел;
IV – множество нечетных не однозначных натуральных чисел;
 |
N
Рис. 3
Задание 6. Число элементов в объединении и разности конечных множеств.
Формулы для подсчета числа элементов в объединении и разности конечных множеств можно использовать для решения текстовых задач определенного вида, что предполагает знание этих формул и владение теоретико-множественными понятиями.
Задача. В классе английский язык изучают 25 человек, а немецкий – 27 человек, причем 18 человек изучают одновременно английский и немецкий языки. Сколько всего человек в классе изучают эти иностранные языки? Сколько человек изучают только английский язык? Только немецкий язык?
Решение. Пусть А – множество школьников, изучающих английский язык, В – множество школьников, изучающих немецкий язык, тогда множество школьников, изучающих два языка – А∩В. По условию задачи: n(А)=25, n(В)=27, n(А∩В)=18.
Требуется найти число учащихся класса, которые изучают эти иностранные языки, а также число учащихся класса, которые изучают только английский язык, только немецкий язык.
1 способ.
1) АÈВ – множество учащихся класса, которые изучают эти иностранные языки. Чтобы найти число элементов этого множества воспользуемся общей формулой для подсчета числа элементов в объединении конечных множеств:
n(АÈВ) = n(А)+n(В)-n(А∩В) = 25+27-18 = 34.
2) Английский язык изучают 25 человек, но среди них 18 человек изучают и немецкий язык. Чтобы найти число учащихся класса, которые изучают только английский язык, воспользуемся формулой для подсчета числа элементов разности конечных множеств. По условию (А∩В) Ì А, следовательно, n(А/(А∩В)) = n(А)-n(А∩В) = 25-18 = 7.
3) Немецкий язык изучают 27 человек, но среди них 18 человек изучают и английский язык. Чтобы найти число учащихся класса, которые изучают только немецкий язык, воспользуемся формулой для подсчета числа элементов разности конечных множеств. По условию (А∩В) Ì В, следовательно, n(В/(А∩В)) = n(В)-n(А∩В) = 27-18 = 9.
2 способ.
Изобразим данные множества при помощи кругов Эйлера и определим число элементов в каждом из непересекающихся подмножеств. Так как два языка изучают 18 школьников, то пересечение множеств А и В содержит 18 элементов. Английский язык изучают 25 человек, но среди них 18 человек изучают и немецкий язык, значит, только английский язык изучают 7 человек (25-18 = 7), укажем это число на кругах Эйлера. Рассуждая аналогично, получим, что только немецкий язык изучают 27 – 18 = 9 человек, укажем это число на кругах Эйлера. Теперь известно количество элементов в каждом из непересекающихся подмножеств, изображенных на кругах Эйлера. Чтобы ответить на первый вопрос задачи нужно сложить все числа: 7 + 18 + 9 = 34.
Рис. 4
Ответ: 34 человека в классе изучают иностранные языки, 7 изучают только английский язык, 9 изучают только немецкий язык.