Рассмотрим систему материальных точек 
на которые действуют активные силы 
с проекциями на неподвижные оси координат 
. В общем случае перемещения точек системы будут стеснены наложенными на систему связями, поэтому не могут быть произвольными. Действие на точки системы связей эквивалентно действию некоторых сил, которые называются силами реакций и обозначаются через 
Проекции этих сил на неподвижные оси координат обозначим через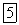 
. В соответствии с одной из основных аксиом механики связи, наложенные на систему материальных точек, могут быть заменены силами реакций. После такой замены система может рассматриваться как свободная от связей.
Будем предполагать, что на систему материальных точек наложены идеальные связи, т. е. связи, сумма работ реакций которых на любом возможном перемещении системы равна нулю, что аналитически можно записать в виде равенства
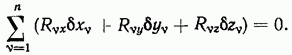
Заменив связи, наложенные на систему, силами, можно записать уравнения движения для каждой точки системы
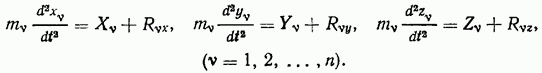
Разрешая эти уравнения относительно реакций связей и подставляя полученные значения в уравнение, определяющее идеальные связи, получим равенство
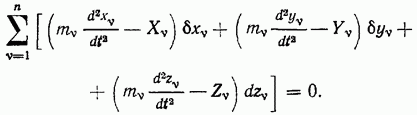
Равенство (а) имеет место для всех возможных перемещений системы. Оно, как видно из вывода, является необходимым условием для действительного движения механической системы. Можно показать и его достаточность, т. е. что соотношение (а) выполняется только для действительных движений (определяет действительное движение системы). Для доказательства к активным силам, действующим на систему, добавим силы реакции связей, после чего будем рассматривать систему как свободную
от связей. Для такой системы допустимы любые возможные перемещения. Обозначив теперь через 
возможные перемещения «освобожденной» системы, будем иметь
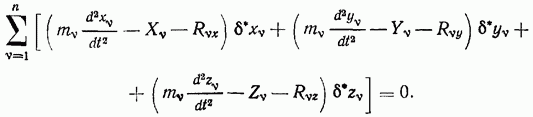
В силу того, что теперь величины 
независимы и произвольны, отсюда получим
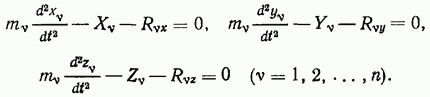
Последние равенства определяют действительное движение системы материальных точек, чем и доказывается достаточность уравнения 
Уравнение (а) является общим уравнением динамики системы материальных точек и было впервые установлено Лагранжем. Впоследствии это уравнение стали называть принципом Даламбера — Лагранжа, или принципом Даламбера. Оно охватывает все движения механических систем с идеальными связями. Принцип Даламбера—Лагранжа заключается в том, что уравнение (а) является необходимым и достаточным условием действительного движения механической системы.
Исходя из общего уравнения динамики, можно решать все задачи о движении механических систем. Оно не содержит реакций связей, а следовательно, дает возможность решать задачи о движении механической системы, не определяя этих реакций. Величины 
представляют собой возможные перемещения точек системы, т. е. те перемещения, которые допускаются связями в данный момент времени. Для каждого конкретного возможного перемещения общее уравнение дает одно дифференциальное уравнение движения системы. Перебирая различные возможные перемещения, получим полную систему дифференциальных уравнений движения системы.
Пример 82. Рассмотрим движение системы, состоящей из двух призм, одна из которых, с массой М, может свободно скользить по гладкой горизонтальной плоскости, а вторая, с массой 
под действием силы тяжести скользит без трения по первой (рис. 183).
Положение системы можно полностью определить двумя параметрами 
которые можно изменять независимо один от другого. Рассмотрим
сначала возможное перемещение, соответствующее изменению только параметра 
оставляя параметр 
неизменным. Обозначая через 
вторые производные по времени от величин 
запишем уравнение для рассматриваемого перемещения
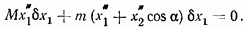
Отсюда, сокращая на 
получим дифференциальное уравнение движения
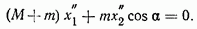
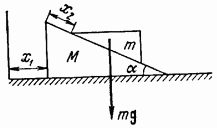
Рис. 183
Рассматривая далее возможное перемещение, при котором изменяется параметр 
и не меняется 
будем иметь
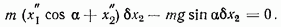
Отсюда, после сокращения на 
получим второе дифференциальное уравнение движения
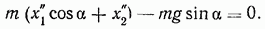
Замечание. Все члены уравнения (а) имеют размерность работы, поэтому можно сказать, что общее уравнение динамики устанавливает равенство нулю работы активных сил и сил инерции Даламбера
на всех возможных перемещениях системы.