Механические колебания – движения, которые точно или приблизительно точно повторяются через определенные интервалы времени. Для колебаний характерно, что колеблющееся тело попеременно смещается то в одну, то в другую сторону относительно некоторой точки или линии – положения равновесия.
Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют:
Колебательная система – система тел, способная совершать свободные колебания.
Одно из основных общих свойств всех колебательных систем заключается в возникновении силы, возвращающей систему в положение устойчивого равновесия.
Рассмотрим примеры колебательных систем:
Маятник – твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.
1) Математический маятник – материальная точка, подвешенная на длинной прочной нерастяжимой невесомой нити.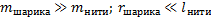 
. → модель.
| В устойчивом положении равновесия силы, действующие на тело, взаимно уравновешены: сила тяжести 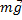 уравновешена силой натяжения нити маятника  .
|
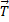| Если отклонить шарик от положения равновесия, то равнодействующая сил тяжести и натяжения нити будет направлена к положению равновесия и под ее действием шарик начнет двигаться с ускорением. |
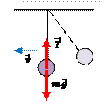
| В момент, когда шарик достигнет положения равновесия сумма всех сил, действующих на него, станет равной нулю. Следовательно, и ускорение шарика, согласно II закону Ньютона станет равным нулю. Но к этому моменту скорость шарика уже достигнет некоторого значения. Согласно закону инерции, любое тело обладает свойством сохранять свою скорость, если на него не действуют силы или равнодействующая сил равна нулю. Поэтому, не останавливаясь в положении равновесия, шарик по инерции будет двигаться. |
 
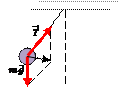
| После прохождения положения равновесия, равнодействующая сил, а значит и ускорение, будет направлена противоположно скорости. Следовательно, шарик будет двигаться замедленно, до тех пор, пока не остановится. После этого шарик начнет ускоренное движение в противоположную сторону. |
| Проскакивая по инерции положение равновесия, шарик продолжит свое движение, после чего весь колебательный процесс повторяется сначала. |
При колебаниях математического маятника шарик всегда движется по дуге окружности, радиус которой равен длине нити l. Поэтому положение шарика в любой момент времени определяется углом отклонение нити от вертикали. Будем считать α положительным, если маятник отклонен вправо от положения равновесия, и отрицательным, если он отклонен влево.
Для того чтобы вывести уравнение движения математического маятника, воспользуемся II законом Ньютона:
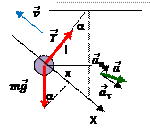
OX: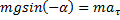 
Проекция силы тяжести на ось ОХ и будет силой, возвращающей маятник в положение равновесия. Причем эта сила всегда имеет знак, противоположный знаку угла: при отклонении маятника вправо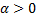 
, проекция силы тяжести на ось ОХ направлена влево 
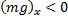; при отклонении маятника влево 
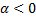, проекция силы тяжести на ось ОХ направлена вправо 
.
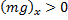Из прямоугольного треугольника: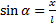 
, тогда: 
Т.к.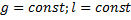 
, то введем обозначение 
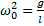, тогда:
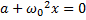- уравнение колебаний математического маятника.
2) Пружинный маятник – материальная точка, подвешенная на упругой невесомой пружине. 
. → модель.
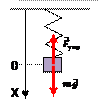
| В устойчивом положении равновесия силы, действующие на тело, взаимно уравновешены: сила тяжести 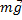уравновешена силой упругости пружины  .
|
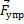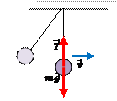
| Если сместить грузик вниз так, чтобы длина пружины увеличилась на x, то на тело начнет действовать дополнительная сила упругости, которая согласно закону Гука, пропорциональна удлинению пружины. Будем называть эту силу – квазиупругая сила – геометрическая сумма силы тяжести и силы упругости, действующих на пружинный маятник. Эта сила направлена вверх и под ее воздействием тело будет двигаться с ускорением, направленным вверх, постепенно увеличивая скорость. Квазиупругая сила будет при этом уменьшаться. |
| Дойдя до положения устойчивого равновесия, квазиупругая сила станет равной нулю, и ускорение, согласно II закону Ньютона, также станет равным нулю. Однако тело не остановится, а будет продолжать двигаться вверх по инерции. |
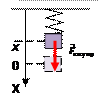
| После прохождения положения равновесия, пружина начинает сжиматься, и в результате вновь появляется квазиупругая сила, направленная уже вниз и тормозящая движение груза. Согласно II закону Ньютона, тело продолжит движение вверх с ускорением, направленным вниз, то есть замедленно. Следовательно, квазиупругая сила стремится вернуть тело в положение равновесия. Скорость убывает до тех пор, пока в самой верхней точке не обратится в ноль. При этом сжатие пружины, а, следовательно, и квазиупругая сила, увеличиваются. |
| После этого тело с ускорением начнет двигаться вниз. С уменьшением х модуль квазиупругой силы убывает и в положении равновесия вновь становится равным нулю. Но тело уже успевает к этому моменту набрать скорость и продолжает двигаться вниз по инерции. Это движение приводит к дальнейшему растяжению пружины. Движение груза тормозиться до полной остановки в крайнем нижнем положении, после чего весь процесс повторяется сначала. |
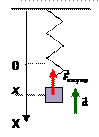Воспользуемся II законом Ньютона для движения пружинного маятника под действием квазиупругой силы:
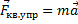
OX: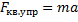 
. Согласно закону Гука: 
Уравнение движения не содержит силы тяжести. Дело в том, что сила тяжести, действуя на груз, вызывает растяжение пружины на постоянную величину. Но это не влияет на характер движения груза.
Т.к.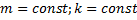 
, то введем обозначение 
, тогда:
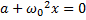- уравнение колебаний пружинного маятника.
Вывод: уравнения движения, описывающие колебания таких различных систем, как груз на пружине и математический маятник, одинаковы. Следовательно, движения этих колебательных систем происходят одинаковым образом. Смещения груза на пружине и шарика маятника от положения равновесия изменяются со временем по одному и тому же закону, несмотря на то, что силы, вызывающие колебания, имеют различную физическую природу. В первом случае это квазиупругая сила, во втором – составляющая силы тяжести.
Величины, характеризующие колебательное движение:
1) Амплитуда (х0) – модуль наибольшего смещения тела от положения равновесия.
Амплитуда определяется начальными условиями.
При колебаниях движение тела периодически повторяется. Колеблющееся тело совершает одно полное колебание, если проходит путь, равный четырем амплитудам.
2) Период (T) – минимальный промежуток времени, через который движение тела полностью повторяется.
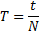
t – время колебаний; N – число полных колебаний.
Си: [T] → 1с.
3) Частота (ν) – число колебаний в единицу времени.
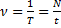Си: [ν] → 1/с = 1Гц.
4) Циклическая (круговая) частота (ω0) – число колебаний за 2π секунд.
Си: [ 
] → 1 рад/с
Эту частоту называют:
Собственная частота (ω0) – частота свободных колебаний.
Согласно уравнению колебаний математического маятника, эта величина равна:
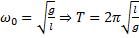
Период колебаний математического маятника зависит:
1) От длины маятника.
Чем больше длина маятника, тем медленнее происходят его колебания. Маятник 1 колеблется медленнее маятника 2.
2) От ускорения свободного падения.
Чем меньше ускорение свободного падения, тем больше период колебаний маятника, и, следовательно, тем медленнее идут часы с маятником. Так часы с маятником в виде груз на стержне отстанут за счет уменьшения ускорения свободного падения с высотой в сутки почти на 7с, если их поднять на вершину Останкинской телебашни (500м).
Период колебаний математического маятника не зависит:
1) От массы маятника.
Маятники 1 и 2 будут совершать одинаковое число колебаний в единицу времени.
1) От амплитуды колебаний (при малых углах отклонения).
Это свойство независимости периода колебаний от амплитуды называют изохронность.
Пусть амплитуда колебаний увеличилась в 2 раза → сила, возвращающая тело в положение равновесия увеличилась в 2 раза → ускорение, вызванное этой силой, увеличилось в 2 раза → приобретенная скорость станет больше в два раза → за то же время тело пройдет вдвое больший путь к положению равновесия, что и при колебаниях вдвое меньшей амплитуды.
Согласно уравнению колебаний пружинного маятника, собственная частота равна:
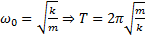
Период колебаний пружинного маятника зависит:
1) От массы маятника.
Чем больше масса маятника, тем медленнее он изменяет свою скорость под действием силы, тем медленнее происходят его колебания. Маятник 1 колеблется медленнее маятника 2.
2) 
От жесткости пружины.
Более жесткая пружина сообщает телу большее ускорение, т.е. быстрее меняет его скорость и, следовательно, уменьшает время одного колебания. Маятник 1 колеблется медленнее маятника 2.
Период колебаний математического маятника не зависит:
1) От амплитуды колебаний (при упругих деформациях).
5) Фаза колебаний (φ) – физическая величина, однозначно определяющая положение колебательной системы в любой момент времени.
Си: [ 
]→ 1 рад
 
| 
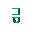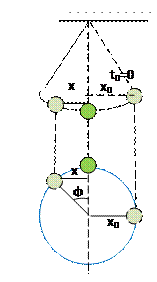
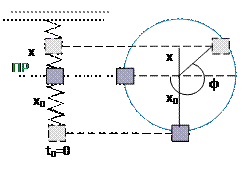
| Проведем вспомогательную окружность радиуса x0. Спроецируем начальное положение тела, и положение тела в момент времени t на эту окружность. Фаза характеризует смещение от положения равновесия (ПР) (или от начального положения) и равна углу между двумя положениями тела на вспомогательной окружности Фаза отсчитывается против часовой стрелки. |
; 
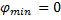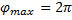
Начальная фаза колебаний (φ0) – фаза колебаний в начальный момент времени (t=0).
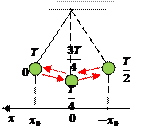
Пусть маятники колеблются с одинаковой частотой и одинаковыми амплитудами. Различают следующие случаи:
| В любой момент времени скорости маятников направлены в противоположные стороны → колебания происходят в противоположных фазах. |
| В любой момент времени скорости маятников направлены в одну сторону → колебания происходят в одинаковых фазах. |
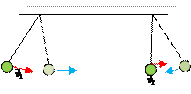
| В некоторый момент времени направления скоростей маятников совпадают. Через какое-то время скорости направлены в разные стороны → колебания происходят с разностью фаз. |
Основная задача механики заключается в нахождении положения тела в любой момент времени. Следовательно, необходимо получить зависимость х=х(t) для математического и пружинного маятников. Для этого необходимо решить уравнение колебаний. Однако математическое решение этих уравнение – задача сложная и требует знаний высшей математики.
Для нахождения зависимости координаты от времени обратимся к вспомогательной окружности. Для математического маятника из прямоугольного треугольника:
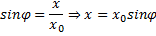
Для пружинного маятника из прямоугольного треугольника:
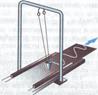
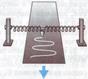Полученную зависимость можно доказать экспериментально. Для этого массивный сосуд с маленьким отверстием снизу подвешивают на нити. Под сосудом находится длинная бумажная лента. В сосуд насыпают песок и приводят в колебательное движение. Если ленту перемещать с постоянной скоростью в направлении, перпендикулярном плоскости колебаний, то на ней останется волнообразная дорожка песка, каждая точка которой соответствует положению колеблющегося груза в тот момент, когда он проходил над ней. Полученная кривая называется синусоидой. Аналогичная кривая получается для груза, подвешенного на пружине.
Гармонические колебания – периодические изменения физической величины в зависимости от времени по закону синуса или косинуса.
Гармонические колебания происходят под действием силы, пропорциональной смещению колеблющейся точки и направленной противоположно этому смещению.
Таким образом, решением уравнения колебания пружинного и математического маятников является функция:
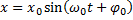либо 
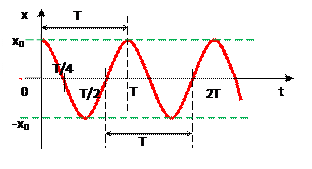где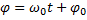 
- фаза колебаний.
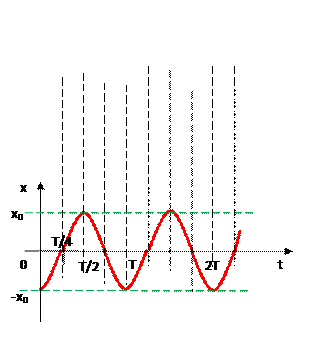
Данную зависимость можно представить графически. График зависимости координаты тела от времени 
имеет вид:
Наибольшие отклонения груза от положения равновесия в обе стороны одинаковы по модулю и равны х0. Маятник начал движение из крайней точки с координатой х = х0. За время, равное периоду, маятник совершил полное колебание, т.е., миновав положение равновесия, дошел до противоположной крайней точки с координатой – х0, на мгновенье задержался в ней, изменил направление скорости на противоположное, затем пошел в обратном направлении и, вторично пройдя через положение равновесия, вернулся в то же самое место, откуда начал движение. Затем колебания повторяются.
При колебательном движении маятников скорость и ускорение меняются со временем (т.е. движение не является равноускоренным), так как меняется величина и направление силы, возвращающей тело в положение равновесия. Рассмотрим характер этого изменения для математического маятника. В начальный момент времени маятник отклонили от положения равновесия.
| t | T/4 | T/2 | 3T/4 | T | |
| x | x0 | 0 | -x0 | 0 | x0 |
| Vx | 0 | -Vmax | 0 | Vmax | 0 |
| Fx | -Fmax | 0 | Fmax | 0 | -Fmax |
| ax | -amax | 0 | amax | 0 | -amax |
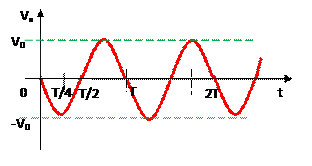Следовательно, зависимость скорости от времени и ускорения от времени также будет периодической.
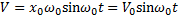
где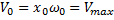 
- амплитуда скорости.
где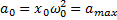 
- амплитуда ускорения.
Построим графики соответствующих колебаний.