ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ
ВОГНУТОЙ ПОВЕРХНОСТИ
МЕТОДОМ КАТАЮЩЕГОСЯ ШАРИКА
Цель работы: Определить радиус кривизны вогнутой сферической поверхности и произвести оценку погрешности полученного результата.
Принадлежности: Вогнутое сферическое зеркало, стальные шарики, секундомер, штангенциркуль.
КРАТКАЯ ТЕОРИЯ
Движение шарика, катящегося по плоской поверхности, можно представить в виде векторной суммы двух движений: 1) поступательного со скоростью uс, равной скорости его центра масс, 2) вращательного вокруг оси, проходящей через центр масс, с угловой скоростью w.
Скорость любой точки шарика относительно поверхности определится соотношением
.  . (1)
. (1)
Если качение шарика происходит без проскальзывания, то скорость его точки B, соприкасающейся с поверхностью, будет равна нулю. В силу этого, как следует из (1) (см. рис.1), 0 = uс - w× r. Поэтому
 , (2)
, (2)
где r - радиус шарика.
С помощью формул (1) и (2), можно подсчитать скорость любой точки шарика. Так, например, скорость точки А равна 2u с.
Шарик, помещенный на вогнутую поверхность, занимает положение, соответствующее минимуму его потенциальной энергии. Если шарик вывести из этого положения и отпустить, то он будет колебаться около своего положения равновесия. Качение шарика без проскальзывания возможно при действии на него со стороны поверхности силы трения покоя (силы трения сцепления) Ft (рис.2). Эта сила Ft может принимать любое значение от 0 до m×N, где m - коэффициент трения, N – величина нормальной реакции поверхности. При качении сила Ft принимает такое значение, при котором скольжение отсутствует. Если сила требующаяся для этого, превышает величину m×N, то чистое качение невозможно - оно будет сопровождаться проскальзыванием.
Покажем, что на вогнутой сферической поверхности при небольших смещениях от положения равновесия, шарик будет совершать гармонические колебания. Результирующая сил, действующих на шарик (силы трения сцепления Ft , нормальной реакция поверхности N и силы тяжести mg) сообщает центру масс шарика некоторое ускорение, которое можно представить в виде векторной суммы нормального an и тангенциального a t ускорений:
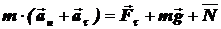 . (3)
. (3)
Проектируя (3) на направление касательной к траектории шарика, получим:

Если ограничиться малыми углами, при которых sina » a, то будем иметь:
 . (4)
. (4)
Результирующий момент сил, действующих на шарик, сообщает ему угловое ускорение b, которое входит в основное уравнению динамики вращающихся твердых тел
 . (5)
. (5)
Уравнение (5) описывает вращение шарика относительно оси, проходящей через его центр масс. Здесь Ic - момент инерции шарика относительно оси, проходящей через центр масс, b - его угловое ускорение шарика, Ft× r - момент силы трения сцепления относительно указанной оси. (Моменты сил mg и N относительно указанной оси равны нулю). Для однородного шара
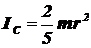 . (6)
. (6)
Если радиус кривизны сферической поверхности R существенно превосходит радиус шарика r, то связь между ускорениями at и b может быть представлена соотношением:
 (7)
(7)
Подставляя (6) и (7) в (5), получим:
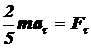 . (8)
. (8)
Исключая величину Ft из формул (4) и (8), можно получить:
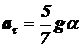 .
.
Принимая во внимание, что
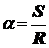 ,
,
где S - смещение шарика от положения равновесия, отсчитанное по траектории центра масс шарика, R - радиус кривизны этой траектории, получим:
 . (9)
. (9)
Из полученного следует, что тангенциальное ускорение шарика пропорционально его смещению от положения равновесия и направлено к положению равновесия. Это указывает на то, что колебания шарика будут гармоническими.
В самом деле, при гармоническом колебании смещение S изменяется по закону
S = A×cosw×t
Дифференцируя S дважды по t, получим:
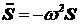 Þ
Þ 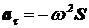 (10)
(10)
Здесь 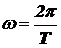 - циклическая частота колебания.
- циклическая частота колебания.
Из формул (9) и (10) следует, что
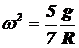
В результате для радиуса кривизны траектории центра масс шарика R получим
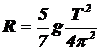 . (11)
. (11)
Радиус кривизны вогнутой поверхности зеркала будет превышать R на величину радиуса шарика r. Поэтому
Rз=R + r. (12)
Чтобы получить более точное выражение для радиуса кривизны сферического зеркала необходимо учесть, что путь S, проходимый центром масс шарика и длина дуги l, описываемая точкой B, не равныдругу. Как следует из рис. 2,
l=a Rз, S=a (Rз-r ) и кроме того l=jr
Дифференцируя приведенные соотношения дважды по t, и принимая во внимание, что тангенциальная составляющая ускорения центра масс шарика at и его угловое ускорение b соответственноравны;
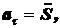 и
и 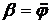 ,
,
получим формулу, связывающую их между собой
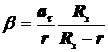 (7’)
(7’)
Используя вместо (7) формулу (7’), получим более точное выражение для радиуса кривизны зеркала
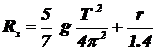 (12’)
(12’)
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Протереть зеркало и шарик чистой фланелевой салфеткой.
2. Определить период колебаний шариков разных размеров, измеряя секундомером время 5 – 10 их колебаний на вогнутой поверхности зеркала.
3. Используя средние значения периодов колебаний шариков разных размеров, по формуле (10) подсчитать R.
4. При помощи штангенциркуля или микрометра определить радиусы шариков r1, r2 и... и подсчитать радиус кривизны сферического зеркала по формулам (12). и (12’).
5.Сравнить полученные результаты и произвести оценку погрешности.
6. Разработать геометрический метод оценки радиуса кривизны сферической поверхности. Найти величину радиуса кривизны вогнутого зеркала этим методом. Сравнить полученные результаты между собой и сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Выяснить, что называют переносной, относительной и абсолютной скоростью. Сформулировать классический закон сложения скоростей.
2. Доказать справедливость соотношения (2). При каком условии оно выполняется?
3. Сформулировать основной закон динамики для вращающихся твердых тел.
4. Определить условия, при которых тело совершает гармонические колебания. Записать формулы для смещения, скорости и ускорения точки, совершающей гармонические колебания.
5. Вывести формулы (9), (11).,(12) и (12’). Сравнить между собой формулы (7) и (7’). Выяснить условия, при которых они дают практически совпадающие результаты..
6. Решитьзадачу. Небольшое тело может скользить без трения по вогнутой сферической поверхности радиуса R. Определить период малых колебаний этого тела на данной поверхности.
ЛИТЕРАТУРА
1. Хайкин С.Э. Физические основы механики -- М.: Наука. 1971.
2. Савельев И.В. Курс общей физики. -- М.: Наука. 1968. т.1. (и более поздние издания).