Примеры решения задач электростатики
Пусть область 
в 
симметрична относительно начала координат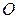 
; в этой области введены сферические координаты 
.(См. Приложение.)
Пусть векторное поле 
обладает свойством:
= 
= 
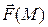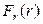
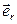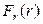
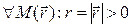(1)
В этом случае говорят, что векторное поле обладает сферической симметрией; обычно используется запись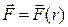 
.
Пусть значение скалярного поля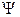 
в любой точке поля 
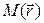зависит только от 
. В этом случае говорят, что скалярное поле 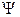обладает сферической симметрией; обычно используется запись 
.
Если точка 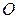принадлежит области определения векторного поля 
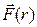, то
, (2)
или, что то же,
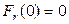. (2+)
Действительно, если бы вектор был отличен от нуля в точке (центре симметрии), то он имел бы в этой точке некоторое определенное направление (в силу однозначности вектор-функции ); тем самым это направление было бы выделенным и симметрия была бы нарушена.
Пусть 
- дифференцируемое скалярное поле. Тогда
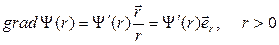(3)
Векторное поле 
обладает сферической симметрией; следовательно, если это поле определено в точке 
, то в силу (2)
(4)
или
. (4+)
(объясните).
Будем рассматривать задачи на нахождение векторов электрического поля 
и электростатического потенциала 
, если известны распределение заряда и свойства среды.
В задачах со сферической симметрией будем полагать, что система зарядов находится в ограниченной области пространства, суммарный заряд системы конечен.
Применение электростатической теоремы Гаусса в условиях сферической симметрии. Нахождение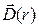 
.
Пусть распределение заряда обладает сферической симметрией. Пусть известны объемная плотность заряда 
и относительная диэлектрическая проницаемость среды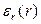 
.
Фиксируем некоторое значение координаты 
и найдем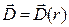 
. Для этого введем вспомогательную Гауссову поверхность 
в виде сферы радиуса 
с центром в начале координат. В соответствии с электростатической теоремой Гаусса
, (5)
где 
- заряд, находящийся внутри поверхности .
В силу сферической симметрии во всех точках поверхности вектор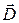 
имеет одинаковую абсолютную величину и представляется в виде:
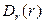
. (6)
Поэтому поток вектора 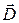через поверхность в левой части соотношения (5) определяется выражением:
(7)
Из (5) и (7) получаем:
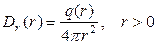. (8)
Рассмотрим различные случаи распределения заряда при наличии сферической симметрии. Будем считать, что заряженные тела не являются проводниками (этот случай рассмотрим отдельно).
А. В начале координат расположен точечный заряд 
.
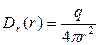, . (9)
Точка 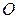- особая точка поля .
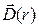Б. Заряд распределен равномерно на сфере радиуса 
.
. (10)
В. Заряжено объемное тело: шар или система шаровых слоев. При этом объемная плотность заряда 
- кусочно непрерывная функция.
Выразим через объемную плотность заряда (см. Приложение).
. (11)
Здесь 
- переменная интегрирования.
Замечание 1. При решении конкретной задачи бывает легче найти заряд из физических соображений, чем формальным интегрированием из (11).
Из соотношений (8) и (11) получаем:
, . (12)
Замечание 2. При решении конкретной задачи бывает проще не формально рассчитать интеграл (12), а осмысленно применить к своей задаче теорему Гаусса, следуя описанной здесь методике (начиная с соотношения (5))
Поле 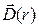, создаваемое объемным телом, не имеет особых точек и определено во всех точках пространства, включая начало координат. В силу свойства (2+) имеем
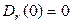. (13)
Кроме того, поле 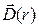, создаваемое объемным телом, является непрерывной функцией; следовательно,
. (14)
Итак, кусочно-непрерывная объемная плотность заряда при наличии сферической симметрии удовлетворяет соотношению (14), а также ограничению
, (15)
которое обусловлено конечностью суммарного заряда рассматриваемой системы тел.
Нахождение напряженности 
, вектора поляризованности 
и электростатического потенциала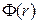 
.
Будем полагать, что среда является линейной, изотропной, не сегнетоэлектрической. Напряженность 
электрического поля связана с индукцией соотношением:
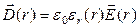. (16)
Относительная диэлектрическая проницаемость среды 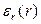- скалярная функция, удовлетворяющая ограничению:
. (17)
Имеет место соотношение
, (18)
где 
- вектор поляризованности.
Соотношение
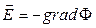(19)
в условиях сферической симметрии принимает вид:
. (19+)
Воспользуемся известной формулой для потенциала в произвольной точке :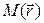
, (20)
где 
- точка, в которой мы полагаем потенциал равным нулю.
Так мы полагаем, что заряды сосредоточены в ограниченной области пространства, естественно положить потенциал равным нулю на бесконечности.
Учитывая сказанное и принимая во внимание сферическую симметрию, соотношение (20) запишем в виде:
. (21)
Задача 1. Шаровой слой с внутренним радиусом 
и внешним радиусом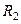 
заряжен с плотностью 
. Слой заполнен диэлектриком с относительной диэлектрической проницаемостью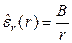 
, 
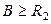. Слой помещен в вакуум.
Здесь 
и 
- константы соответствующих размерностей; укажите эти размерности. Объясните ограничение 
.
Найдите векторы электрического поля 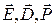и электростатический потенциал 
. Изобразите эскизы графиков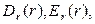 
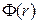, рассмотрев различные знаки константы .
Решение. Совместим начало координат с центром шарового слоя. Ясно, что задача обладает сферической симметрией. Следовательно, искомые поля обладают соответствующими свойствами (см. выше).
Объемная плотность, соответствующая рассматриваемому распределению заряда, задается кусочно непрерывной функцией:
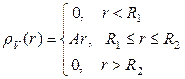. (22)
Относительная диэлектрическая проницаемость среды задается кусочно непрерывной функцией:
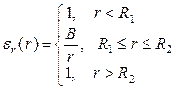. (23)