Фиксируем некоторое значение координаты 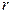 и найдем
и найдем  . Для этого введем вспомогательную Гауссову поверхность
. Для этого введем вспомогательную Гауссову поверхность  в виде сферы радиуса
в виде сферы радиуса  с центром в начале координат. В соответствии с электростатической теоремой Гаусса
с центром в начале координат. В соответствии с электростатической теоремой Гаусса
 , (*)
, (*)
где  - заряд, сосредоточенный внутри поверхности
- заряд, сосредоточенный внутри поверхности  .
.
Из (*) следует (см. равенства (5)-(8)):
 ,
,  .
.
В рассматриваемой задаче
 .
.
Таким образом,
 , (61)
, (61)
 .
.
 , (62)
, (62)
 .
.
Потенциал рассчитываем по формуле (21). Имеем:
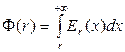
 (63)
(63)
2. Задачи, обладающие цилиндрической (азимутальной) симметрией. Случай отсутствия зависимости полей от продольной координаты  .
.
Пусть введены цилиндрические координаты  . (См. Приложение. Не путайте координату
. (См. Приложение. Не путайте координату  со сферической координатой, обозначенной той же буквой.) Пусть область
со сферической координатой, обозначенной той же буквой.) Пусть область  в
в  обладает азимутальной симметрией (т.е. симметрией по углу
обладает азимутальной симметрией (т.е. симметрией по углу  ). Ось симметрии – ось
). Ось симметрии – ось  .
.
Будем рассматривать скалярные поля, зависящие только от полярного радиуса  , и векторные поля, обладающие свойством:
, и векторные поля, обладающие свойством:
 =
= 

 . (1)
. (1)
Здесь  - орт (в точке М) цилиндрической системы координат. Понятно, что такие векторные и скалярные поля обладают азимутальной симметрией: их значения не зависят от полярного угла
- орт (в точке М) цилиндрической системы координат. Понятно, что такие векторные и скалярные поля обладают азимутальной симметрией: их значения не зависят от полярного угла  .
.
Если ось  принадлежит области определения векторного поля
принадлежит области определения векторного поля  , то
, то
 . (2)
. (2)
Действительно, если бы вектор  был отличен от нуля на оси симметрии, то он имел бы в точках этой оси некоторое определенное направление (в силу однозначности вектор-функции
был отличен от нуля на оси симметрии, то он имел бы в точках этой оси некоторое определенное направление (в силу однозначности вектор-функции  ); тем самым это направление было бы выделенным и симметрия была бы нарушена, появилась бы зависимость поля от угла
); тем самым это направление было бы выделенным и симметрия была бы нарушена, появилась бы зависимость поля от угла  .
.
Будем рассматривать задачи на нахождение векторов электрического поля  и электростатического потенциала
и электростатического потенциала  , если известны распределение заряда и свойства среды.
, если известны распределение заряда и свойства среды.
Заметим, что зависимость полей только от полярного радиуса имеет место в том случае, если электростатическое поле создается азимутально-симметричными системами зарядов, имеющими бесконечную протяженность вдоль оси  (цилиндр, цилиндрическая поверхность, нить и т.п.). Именно этот случай мы и будем рассматривать.
(цилиндр, цилиндрическая поверхность, нить и т.п.). Именно этот случай мы и будем рассматривать.
Применение электростатической теоремы Гаусса. Нахождение  .
.
Пусть известны объемная плотность заряда  и относительная диэлектрическая проницаемость среды
и относительная диэлектрическая проницаемость среды  . (Здесь
. (Здесь  - полярный радиус).
- полярный радиус).
Фиксируем некоторое значение координаты  и найдем
и найдем  . Для этого введем вспомогательную Гауссову поверхность
. Для этого введем вспомогательную Гауссову поверхность  в виде цилиндра единичной длины радиуса
в виде цилиндра единичной длины радиуса  , ось симметрии которого совпадает с осью
, ось симметрии которого совпадает с осью  . В соответствии с электростатической теоремой Гаусса
. В соответствии с электростатической теоремой Гаусса
 , (5)
, (5)
где  - заряд, находящийся внутри поверхности
- заряд, находящийся внутри поверхности  .(Индекс 1 подсказывает, что заряд находится в цилиндре единичной длины.)
.(Индекс 1 подсказывает, что заряд находится в цилиндре единичной длины.)
Поток вектора  через торцы цилиндра
через торцы цилиндра  равен нулю. (подумайте, почему.)
равен нулю. (подумайте, почему.)
Во всех точках боковой поверхности  цилиндра
цилиндра  вектор
вектор  имеет одинаковую абсолютную величину и представляется в виде:
имеет одинаковую абсолютную величину и представляется в виде:


 . (6)
. (6)
Поэтому поток вектора  через поверхность
через поверхность  в левой части соотношения (5) определяется выражением:
в левой части соотношения (5) определяется выражением:
 (7)
(7)
Из (5) и (7) получаем:
 . (8)
. (8)
Замечание. При решении конкретной задачи бывает проще не формально воспользоваться формулой (8), а осмысленно применить к своей задаче теорему Гаусса, следуя описанной здесь методике (начиная с соотношения (5))
Нахождение напряженности  , вектора поляризованности
, вектора поляризованности  и электростатического потенциала
и электростатического потенциала  .
.
Будем полагать, что среда является линейной, изотропной, не сегнетоэлектрической. Напряженность  электрического поля связана с индукцией соотношением:
электрического поля связана с индукцией соотношением:
 . (9)
. (9)
Относительная диэлектрическая проницаемость среды  - скалярная функция, удовлетворяющая ограничению:
- скалярная функция, удовлетворяющая ограничению:
 .
.
Имеет место соотношение
 , (10)
, (10)
где  - вектор поляризованности.
- вектор поляризованности.
Соотношение
 (11)
(11)
в условиях зависимости полей только от полярного радиуса  принимает вид:
принимает вид:
 . (12)
. (12)
Воспользуемся известной формулой для потенциала в произвольной точке  :
:
 , (13)
, (13)
где 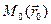 - точка, в которой мы полагаем потенциал равным нулю.
- точка, в которой мы полагаем потенциал равным нулю.
Мы рассматриваем здесь заряженные тела, имеющие бесконечную протяженность вдоль оси  . Поэтому потенциал не может считаться равным нулю на бесконечности (мы это покажем на примере). Соотношение (13) запишем в виде:
. Поэтому потенциал не может считаться равным нулю на бесконечности (мы это покажем на примере). Соотношение (13) запишем в виде:
 , (14)
, (14)
считая  ,
,  .
.
Пример. Заряд распределен равномерно с объемной плотностью  в бесконечном цилиндре радиуса
в бесконечном цилиндре радиуса  . Среда: вакуум.
. Среда: вакуум.
Совместим ось  с осью цилиндра. Изобразим схематично картину поля в плоскости, перпендикулярной оси
с осью цилиндра. Изобразим схематично картину поля в плоскости, перпендикулярной оси  .
.

Ясно: 


Поле обладает цилиндрической симметрией и не зависит от координаты  .
.
В силу (8)
 .
.
 .
.
Тогда с учетом (9)
 .
.
 =
=  , где
, где  .
.
Так как потенциал определяется с точностью до произвольной постоянной, выбор 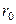 за нами.
за нами.
Если мы положим 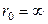 , то
, то  , следовательно,
, следовательно,  , то есть потенциал будет определен некорректно.
, то есть потенциал будет определен некорректно.
Следовательно,  . Положим
. Положим  . Получим:
. Получим:
 .
.


