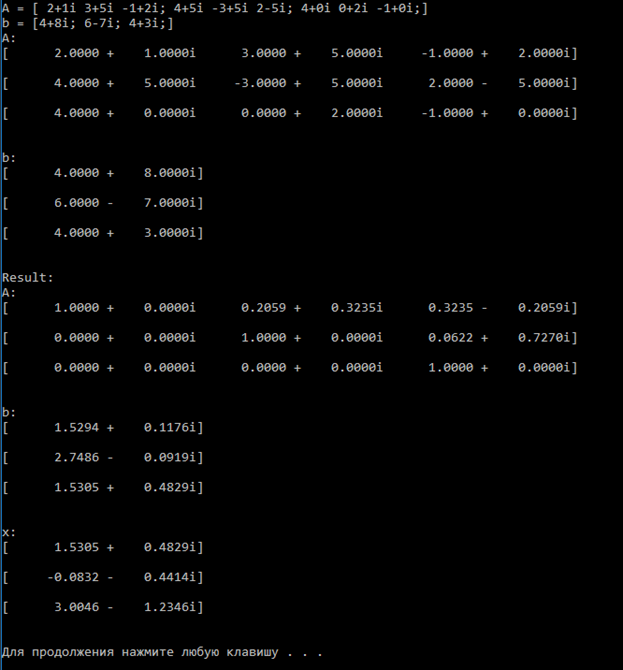
Рисунок 3 — Решение контрольной задачи в программе
Как видно из представленных скриншотов разработанное программное обеспечение позволяет решать СЛАУ с помощью матриц. При этом программа предоставляет достаточную точность результатов, о чём свидетельствует проверка при помощи калькулятора или иного программного обеспечения. Программа реализует все операции над комплексными числами, поэтому пользоваться ими ничуть не сложнее, чем вещественными. При этом достигается хорошая скорость предоставления результата решения.
РЕШЕНИЕ ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ

Рисунок 4 — Исходная матрица в программе

Рисунок 5 — Решение задачи повышенной сложности в программе

Рисунок 6 — Исходная матрица в MATLAB

Рисунок 7 — Решение задачи повышенной сложности в MATLAB
Как видно из представленных выше рисунков, разработанное программное обеспечение реализует метод Гаусса для решения СЛАУ и при этом обладает точностью решения сопоставимой с MATLAB.
ЗАКЛЮЧЕНИЕ
При написании курсовой работы была изучена проблемы вычисления значений корней систем линейных алгебраических уравнений и один из методов для реализации этого решения на вычислительных машинах.
Метод Гаусса обладает достаточно большой скоростью при обработке матриц, построенных из СЛАУ, малых размеров, однако, как выяснилось, не очень хорошо справляется при больших размерностях. Также основным недостатком метода Гаусса является невозможность обработки матриц с нулевыми элементами на главной диагонали. Однако, этот недостаток устраняется при реализации выбора ведущего элемента, который несколько замедляет выполнение программы, но делает результат более точным, а сам алгоритм более устойчивым.
Разработанное программное обеспечение продемонстрировало хорошие и точные результаты для матриц малых размеров, что вполне соответствует ожиданиям при реализации метода Гаусса.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1 Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы: учеб. пособие. - М.: Издательский дом МЭИ, 2008. – 672 с.
2 Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: учеб. пособие для вузов. - М.: БИНОМ. Лаборатория знаний, 2006. – 624 с.
3 Турчак Л.И., Плотников П.В. Основы численных методов: учеб. пособие. - М.: Физматлит, 2005.
4 Бьёрн Страуструп. Язык программирования C++ = TheC++ ProgrammingLanguage / Пер. с англ. — 3-е изд. — СПб.; М.: Невский диалект — Бином, 1999. — 991 с. — 3000 экз. — ISBN 5-7940-0031-7 (Невский диалект), ISBN 5-7989-0127-0 (Бином), ISBN 0-201-88954-4 (англ.).
5 Бьёрн Страуструп. Язык программирования C++. Специальноеиздание = The C++ programming language. Special edition. — М.: Бином-Пресс, 2007. — 1104 с. — ISBN 5-7989-0223-4.
Приложение А
Листинг
Main.cpp
#include <cstdlib>
#include "matrix.h"
using namespace std;
matrix gauss(const matrix& A, const matrix& b)
{
matrix _A = A;
matrix _b = b;
matrix _x(_A.getSizeM(),1);
vector<int> indexes(_A.getSizeM());
intindex{0};
complex tmp{0,0};
for(inti{0}; i< (int)indexes.size(); i++) indexes[i] = i;
for(int k{0}; k < _A.getSizeN(); k++)
{
index = _A.mainColumn(k);
_A.swapColumn(index,k);
swap(indexes[k], indexes[index]);
tmp = _A[k][k];
for(int j{0}; j < _A.getSizeM(); j++) _A[k][j] = _A[k][j]/tmp;
_b[k][0] = _b[k][0]/tmp;
for(inti{k+1}; i< _A.getSizeN(); i++)
{
tmp = _A[i][k];
for(int j{k}; j < _A.getSizeM(); j++)
{
_A[i][j] = _A[i][j] - _A[k][j] * tmp;
}
_b[i][0] = _b[i][0] - _b[k][0] * tmp;
}
}
cout<<"Result:"<<endl;
cout<<"A:"<<endl<<_A<<endl;
cout<<"b:"<<endl<<_b<<endl;
_x = _b;
for(inti{_A.getSizeN()-1}; i>= 0; i--)
{
for(int j{_A.getSizeM()-1}; j >i; j--)
{
_x[i][0] = _x[i][0] - _x[j][0] * _A[i][j];
}
}
matrix x(_x.getSizeN(),1);
for(inti{0}; i< _x.getSizeN(); i++)
{
x[indexes[i]] = _x[i];
}
return x;
}
intmain() {
matrix A, b;
while(true)
{
cout<<"A = ";
cin>>A;
if(cin.fail() || cin.bad())
{
cin.clear();
cin.sync();
}
else break;
}
while(true)
{
cout<<"b = ";
cin>>b;
if(cin.fail() || cin.bad())
{
cin.clear();
cin.sync();
}
else break;
}
cout<<"A:"<<endl<<A<<endl;
cout<<"b:"<<endl<<b<<endl;
matrix x = gauss(A,b);
cout<<"x:"<<endl<<x<<endl;
system("pause");
return 0;
}
Complex.h
#pragma once
#include <iostream>
#include <iomanip>
#include <cmath>
class complex
{
private:
double re;
double im;
public:
complex();
complex(double, double);
complex(const complex&);
double Re() const;
double Re();
double Im() const;
double Im();
double Abs() const;
complex& operator = (const complex&);
friend complex& operator +(const complex&, const complex&);
friend complex& operator -(const complex&, const complex&);
friend complex& operator /(const complex&, const complex&);
friend complex& operator *(const complex&, const complex&);
friend std::ostream& operator <<(std::ostream&, const complex&);
friend std::istream& operator >>(std::istream&, complex&);
};
std::istream&errorprint(std::istream&, const char*);
Complex.cpp
#include "complex.h"
complex::complex():re{0.0},im{0.0}
{}
complex::complex(double r, double i):re{r},im{i}
{}
complex::complex(const complex& value):re{value.Re()},im{value.Im()}
{}
double complex::Re(){return re;}
double complex::Im(){return im;}
double complex::Re()const{return re;}
double complex::Im()const{return im;}
double complex::Abs() const
{
return double{std::sqrt(re*re+im*im)};
}
complex&complex::operator =(const complex& right)
{
if(this!= &right)
{
re = right.Re();
im = right.Im();
}
return *this;
}
complex& operator + (const complex& left, const complex& right)
{
return (*new complex{left.Re()+right.Re(), left.Im()+right.Im()});
}
complex& operator - (const complex& left, const complex& right)
{
return (*new complex{left.Re()-right.Re(), left.Im()-right.Im()});
}
complex& operator * (const complex& left, const complex& right)
{
double _re = left.Re() * right.Re() - left.Im() * right.Im();
double _im = left.Re() * right.Im() + left.Im() * right.Re();
return *new complex(_re,_im);
}
complex& operator / (const complex& left, const complex& right)
{
double tmp = right.Re() * right.Re() + right.Im() * right.Im();
double _re = (left.Re() * right.Re() + left.Im() * right.Im())/tmp;
double _im = (left.Im() * right.Re() - left.Re() * right.Im())/tmp;
return *new complex(_re,_im);
}
std::ostream& operator <<(std::ostream& out, const complex& value)
{
char op;
double _im = value.im;
if(value.im<0)
{
op = '-';
_im *= (-1);
}
else op = '+';
out<<value.Re()<<std::setw(2)<<op<<std::setw(10)<<_im<<'i';
return out;
}
std::istream& operator >>(std::istream& in, complex& value)
{
char op = ' ', i = ' ';
double _re, _im;
in>>_re>>op>>_im>>i;
if(in.fail())
{
in.clear(std::ios_base::failbit);
}
else if(op!= '-' && op!='+')
{
return errorprint(in,"!!!ERROR: Invalid input(Missing '-' or '+')!!!");
}
else if(i!= 'i') return errorprint(in,"!!!ERROR: Invalid input(Missing 'i')!!!");
else if(in.bad()) std::cout<<"!!!ERROR: Stream is corrupted"<<std::endl;
else
{
if(op == '-') _im *= (-1);
value = complex(_re,_im);
}
return in;
}
std::istream&errorprint(std::istream&in, const char *error)
{
in.clear(std::ios_base::badbit);
std::cout<<error<<std::endl;
return in;
}
Matrix.h
#pragma once
#include "complex.h"
#include <vector>
#include <algorithm>
#include <cstdlib>
#include <string>
class matrix
{
private:
std::vector<std::vector<complex>> array;
intsizeN;
intsizeM;
public:
matrix();
matrix(int);
matrix(int, int);
matrix(const matrix&);
~matrix();
intmainColumn(constint&) const;
void swapColumn(constint&, constint&);
intgetSizeN() const;
intgetSizeM() const;
std::vector<complex>& operator [](int);
matrix& operator = (const matrix&);
friend std::istream& operator >>(std::istream&, matrix&);
friend std::ostream& operator <<(std::ostream&, matrix&);
};
Matrix.cpp
#include "matrix.h"
matrix::matrix():sizeN{0}, sizeM{0}, array{std::vector<std::vector<complex>>(0,std::vector<complex>(0))}
{
}
matrix::matrix(int _size):sizeN{_size}, sizeM{_size}, array{std::vector<std::vector<complex>>(_size,std::vector<complex>(_size))}
{
}
matrix::matrix(int _sizeN, int _sizeM):sizeN{_sizeN}, sizeM{_sizeM}, array{std::vector<std::vector<complex>>(_sizeN,std::vector<complex>(_sizeM))}
{
}
matrix::matrix(const matrix& value):matrix(value.sizeN, value.sizeM)
{
std::copy(value.array.begin(),value.array.end(),array.begin());
}
matrix::~matrix()
{
array.clear();
}
intmatrix::getSizeN() const
{
return sizeN;
}
intmatrix::getSizeM() const
{
return sizeM;
}
intmatrix::mainColumn(constint& index) const
{
int _index{0};
complex max{0,0};
for(inti = index; i<sizeM; i++)
{
if(max.Abs()<array[index][i].Abs())
{
max = array[index][i];
_index = i;
}
}
return _index;
}
void matrix::swapColumn(constint&i, constint& j)
{
for(int z{0}; z <sizeN; z++)
{
std::swap(array[z][i],array[z][j]);
}
}
std::vector<complex>& matrix::operator [] (inti)
{
if(i<sizeN&&i>=0) return array[i];
}
matrix&matrix::operator =(const matrix& right)
{
if(this!=&right)
{
sizeN = right.sizeN;
sizeM = right.sizeM;
array = std::vector<std::vector<complex>>(sizeN,std::vector<complex>(sizeM));
std::copy(right.array.begin(),right.array.end(),array.begin());
}
return *this;
}
std::istream& operator >>(std::istream& in, std::vector<complex>&dest)
{
if(dest.size()!=0) dest.clear();
complex _data;
char c = ' ';
inti{0};
for(_data; in>>_data;)
{
dest.push_back(_data);
i++;
}
if(in.bad())
{
std::string err = "!!!ERROR: Invalid element input in column "+std::to_string(i)+"!!!";
return errorprint(in,err.c_str());
}
if(in.fail())
{
in.clear();
in>>c;
if(c!= ';')
{
in.unget();
in.clear(std::ios_base::failbit);
if(dest.size()!= 0)
{
dest.clear();
return errorprint(in,"!!!ERROR: Invalid input(Missing ';')");
}
}
}
return in;
}
std::istream& operator >>(std::istream& in, matrix& value)
{
std::vector<complex> _strdata;
matrix _matdata;
inti{0};
char c = ' ';
in>>c;
if(c!= '[')
{
return errorprint(in,"!!!ERROR: Invalid input(Missing '[')!!!");
}
for(_strdata; in>>_strdata;)
{
_matdata.array.push_back(_strdata);
if(i == 0) _matdata.sizeM = _matdata.array[i].size();
i++;
}
if(in.bad())
{
std::string err = "!!!ERROR: Invalid element input in string "+std::to_string(i)+"!!!";
return errorprint(in,err.c_str());
}
if(in.fail())
{
in.unget();
in.clear();
in>>c;
if(c!= ']') return errorprint(in,"!!!ERROR: Invalid input(Missing ']')!!!");
else
{
_matdata.sizeN = i;
value = _matdata;
}
}
return in;
}
std::ostream& operator <<(std::ostream& out, matrix& value)
{
out.precision(4);
out<<std::fixed;
for(inti{0};i<value.sizeN;i++)
{
out<<"[";
for(int j{0}; j<value.sizeM;j++)
{
out<<std::setw(12)<<value.array[i][j];
}
out<<"]"<<std::endl<<std::endl;
}
return out;
}
Приложение Б