ОПИСАНИЕ ВЫЧИСЛИТЕЛЬНОЙ ПРОБЛЕМЫ

Содержание

ВВЕДЕНИЕ. 4

1 ОПИСАНИЕ ВЫЧИСЛИТЕЛЬНОЙ ПРОБЛЕМЫ.. 6

2 ОПИСАНИЕ ИЗУЧАЕМОГО МЕТОДА.. 8

3 РАЗРАБОТКА СХЕМЫПРОГРАММЫ.. 10

4 РАЗРАБОТКА ЛИСТИНГА ПРОГРАММЫ.. 15

5 РЕШЕНИЕ КОНТРОЛЬНОЙ ЗАДАЧИ.. 17

5.1 Решение вручную.. 17

5.2 Решение с помощью программы.. 19

6 РЕШЕНИЕ ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ.. 21

ЗАКЛЮЧЕНИЕ. 23

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ.. 24

Приложение А.. 25

Приложение Б. 33

ВВЕДЕНИЕ

Численные методы — часть более широкой математической дисциплины, которая называется вычислительной математикой. Вычисления — получение какого-либо ответа в виде чисел, а также получение каких-либо конструктивных и объективных приближений для математической модели.

Математическая модель — отображение в виде формул и данных какого-либо процесса из практики или объективной реальности. Такие модели, как правило, являются достаточно сложными для реализации их решения вручную или напрямую с помощью вычислительных машин.

Для таких случаев пригождается вычислительная математика, которая занимается решением таких типовых задач, как:

- Проблема нахождения приближения того или иного математического объекта для более удобного вычисления.

- Оценка трудоёмкости вычисления объектов из математической модели, способы уменьшить эту трудоёмкость.

- Реализация алгоритмов вычисления математических объектов на конкретных вычислительных машинах.

Поскольку вычислительные машины на самом низком уровне могут оперировать лишь логическими и арифметическими операциями, перед теоретиками и практиками становится задача найти такой алгоритм, который бы в конечном итоге затрагивал только такие типы операций, при этом был достаточно простой для реализации на конкретной машине.

Числовые данные в практических задачах часто бывают не вполне точны, обладая рядом погрешностей. Такое поведение числового представления данных называют ошибкой или погрешностью, т.е. разностью между истинным значением какого-либо объекта из математической модели и его значением на практике представления в процессе вычисления.

Вычислительная математика анализирует математические модели, связанные с применением вычислительных машин в различных областях научной и практической деятельности, разрабатывает методы и алгоритмы для решения типовых задач, возникающих при исследовании этих моделей.

При анализе изучают постановку задачи, выбирают модель, анализируют выходную и выходную информацию, численной решение задач.

Пусть исходная математическая задача поставлена корректно, т.е. ее решение существует, единственно и непрерывно зависит от входных данных. Тогда дискретная модель этой задачи должна быть построена таким образом, чтобы свойство корректности сохранялось. Следовательно, в понятие корректности численного метода включаются свойства однозначной разрешимости соответствующей системы уравнений и ее устойчивости. Под устойчивостью понимается непрерывная зависимость от входных данных.

Вторая группа требований, предъявляемых к численным методам, связана с возможностью реализации данной дискретной модели на данном компьютере, т.е. с возможностью получить численное решение за приемлемое время. Основным препятствием для реализации корректно поставленного алгоритма является ограниченный объем оперативной память ЭВМ и ограниченное время счета.

Для вычислительных машин численные методы должны обладать свойствами экономичности по числу операций и требуемому объёму памяти. Как правило сложные задачи делятся на более лёгкий, средства решения которых давно уже найдены и легко реализуемы на ЭВМ.

ОПИСАНИЕ ВЫЧИСЛИТЕЛЬНОЙ ПРОБЛЕМЫ

К вычислительным задачам линейной алгебры относят задачи решения систем линейных алгебраических уравнений (СЛАУ) 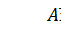, вычисления обратных матриц , вычисления определителей , задачи вычисления собственных чисел и собственных векторов матриц. Эти задачи имеют очень важное теоретическое и прикладное значение. Трудности решения указанных задач, как правило, связаны с большой размерностью матриц. Чаще всего вычислительные задачи линейной алгебры решают точными и итерационными методами:

- Метод называется точным, если в предположении отсутствия ошибок округлений, получается точное решение за конечное число шагов.

- Метод называется итерационным, если решение получается в виде предела элементов некоторой последовательности.

В точных методах матрицу исходной системы уравнений эквивалентными преобразованиями приводят к более простой матрице или раскладывают на произведение более простых матриц. Большинство точных методов относятся к так называемым методам исключения. В этих методах, последовательно исключая неизвестные, исходную систему приводят к системе с треугольной или диагональной матрицей. Очевидно, что последние легко разрешимы.

В общем случае СЛАУ имеет вид:

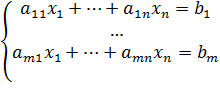
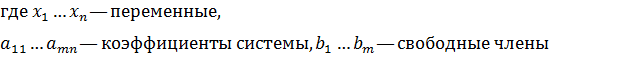
Такие системы разделяются по своим качественным характеристикам на:

- Однородные — все свободные члены равны нулю.

- Неоднородные — хотя бы один свободный член не равен нулю.

- Квадратные — количество переменных равно количеству уравнений.

- Прямоугольные — количество переменных не равно количеству уравнений.

- Недоопределённые — количество переменных меньше количества уравнений.

- Переопределённые — количество переменных больше количества уравнений.

Решением же СЛАУ является нахождение значения количества переменных таких, что при подстановке этих переменных на свои места в систему все уравнения превращаются в тождества. Отсюда следуют, что СЛАУ также можно разделить ещё на несколько категорий:

- Совместные имеют хотя бы одно решение.

- Несовместные не имеют решений.

- Определённые имеют одно решение.

- Неопределённые имеют множество решений.

Самым сложным является реализация решения неопределённых СЛАУ, так как результат решения может зависеть от многих факторов:

- Способ реализации алгоритма.

- Конкретная реализация арифметических и логических операций на вычислительной машине.

- Используемое программное обеспечение.