Решение.
Ясно:
а) 
(2)
б) 
(3)
в) 
(4)
Здесь 
- объемная плотность заряда,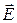 
- напряженность электрического поля.
Таким образом, задача сводится к одномерной (имеется зависимость электрического поля только от переменной 
.)
Очевидна также нечетность компоненты 
относительно плоскости 
:
. (5)
Так как
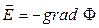
, (6)
соотношение (5) запишем в виде
. (7)
В общем случае потенциал удовлетворяет уравнению
,
где 
- электрическая постоянная, 
- относительная диэлектрическая проницаемость среды. Данное уравнение для однородной изотропной среды имеет вид:
. (8)
Это уравнение Пуассона.
В рассматриваемом случае в силу (2), (3), (4) уравнение (8) запишется в виде:
. (9)
Так как заряд распределен на плоскости, понятно, что объемная плотность заряда является обобщенной функцией. Задача свелась к одномерной, поэтому будем считать, что 
. Другими словами – обобщенная объемная плотность заряда 
- линейный непрерывный функционал, заданный на пространстве основных функций, зависящих только от переменной . Тогда напряженность и потенциал электрического поля – также обобщенные функции: 
.
С учетом сказанного обобщенная объемная плотность заряда при его распределении на плоскости 
с поверхностной плотностью 
имеет вид
, (10)
где 
- 
-функция Дирака.
Уравнение (9) запишется:
. (11)
Граничные условия:
, (12)
(условие для норм. комп-т напряженности на заряж пов-ти) (13)
Воспользуемся известным результатом (для обобщенных функций):
, (14)
где 
- известная функция Хевисайда.
Интегрируя (11), получим:
, (15)
где 
- произвольная постоянная.
Выберем произвольную постоянную с учетом условия (7) нечетности 
относительно плоскости 
. Переходя к «обычным» функциям, получаем:
(16)
(В соотношении (16) нестрогие неравенства в обоих случаях обусловлены тем, что плоскость - двусторонняя поверхность).
(17)
Нетрудно видеть, что граничное условие (13) выполняется.
График функции 
постройте самостоятельно.
Из (17) с учетом условия (12) получаем:
(18)
График функции 
постройте самостоятельно.
Замечание. Дано подробное решение. На экзамене, в курсовой работе пишите кратко. Решение займет несколько строк.
Ц1. Бесконечный круглый металлический цилиндр радиуса 
заряжен; заряд, приходящийся на единицу длины, равен 
. Цилиндр окружен диэлектриком с относительной диэлектрической проницаемостью 
. Найти из уравнения Максвелла вектор электрической индукции. Найти напряженность электрического поля. Построить графики ненулевых компонент 
(для 
). Найти электростатический потенциал 
при условии
. (*)
Решение.
Введем цилиндрические координаты 
. Пусть ось 
совмещена с осью симметрии цилиндра.
Заметим, что рассматриваемая задача обладает цилиндрической симметрией: распределение заряда, свойства среды, а следовательно, и электрическое поле не зависят от полярного угла . Зависимость от координаты также отсутствует (так как цилиндр бесконечен). Поэтому
; 
(1)
Таким образом, задача сводится к одномерной (имеется зависимость электрического поля только от переменной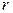 
.)
Уравнение Максвелла
(2)
в цилиндрических координатах имеет вид:
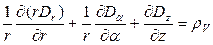. (3)
С учетом (1) уравнение (3) принимает вид:
. (4)
Цилиндр металлический, это проводник. Следовательно, заряд распределен на внешней поверхности с поверхностной плотностью 
. Поэтому объемная плотность заряда представляется обобщенной функцией. Задача свелась к одномерной, поэтому будем считать, что . Другими словами – плотность заряда - линейный непрерывный функционал, заданный на пространстве основных функций, зависящих только от переменной 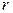. Тогда напряженность и потенциал электрического поля – также обобщенные функции: 
.
С учетом сказанного обобщенная объемная плотность заряда при его распределении на поверхности 
с поверхностной плотностью 
имеет вид
.
Здесь - -функция Дирака.
Уравнение Максвелла принимает вид:
. (5)
Находим решение (5) при условии:
(внутри проводника и на его внутренней поверхности эл. поле отсутствует) (6)
Умножим (5) на 
:
. (7)
Использовано свойство -функции Дирака:
,
где функция 
предполагается непрерывной в окрестности точки 
.
Интегрируя (7) с учетом условия (6), получаем:
,
или, переходя к «обычным» функциям,
. (8)
Здесь - функция Хевисайда.
В соотношении (8) нестрогие неравенства в обоих случаях обусловлены тем, что мы различаем внешнюю и внутреннюю поверхности проводника.
. (9)
График 
постройте самостоятельно.
Найдем 
из уравнения:
(10)
с граничными условиями:
=0 (условие (*) +непрерывность потенциала[1])
Получаем:
.
Примерный график функции 
постройте самостоятельно.
Замечание. На экзамене, в курсовой работе вам может быть предложено (с целью облегчения задания) не находить потенциал, но изобразить эскиз графика .Это легко сделать, принимая во внимание следующие моменты.
.
Следовательно, если на некотором промежутке 
, то на этом промежутке 
возрастает; если на некотором промежутке 
, то на этом промежутке убывает.
Если на некотором промежутке 
возрастает, то на этом промежутке функция выпукла вверх.
Если на некотором промежутке убывает, то на этом промежутке функция выпукла вниз.
Ш1. Шар радиуса 
заряжен равномерно по объему и имеет заряд 
. Внутри шара диэлектрик с относительной диэлектрической проницаемостью 
, вне шара диэлектрик с относительной диэлектрической проницаемостью 
.
Найти из уравнения Максвелла вектор электрической индукции. Найти напряженность электрического поля. Построить графики ненулевых компонент 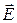(для 
, 
). Найти электростатический потенциал 
. Построить график.
Решение.
Введем сферические координаты 
.
В силу сферической симметрии задачи
; 
; 
. (1)
Уравнение Максвелла
(2)
в сферических координатах имеет вид:
. (3)
С учетом (1) уравнение (3) принимает вид:
. (4)
В рассматриваемой задаче
,
где
. (5)
Тогда уравнение Максвелла принимает вид:
. (6)
Здесь
.
(В данной задаче мы не прибегаем к аппарату обобщенных функций; 
-«обычная» функция.)
Граничные условия для уравнения (6):
А. 
(при 
имеем поле точечного заряда) (7)
Б. Граничное условие для нормальной компоненты 
на поверхности 
запишется:
,
где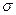 
- плотность поверхностного заряда на указанной поверхности. Так как шар заряжен по объему и поверхностного заряда на его границе нет, имеем
. (8)
Нахождение 
и .
Умножим (6) на 
:
. (9)
Интегрируя (9) с учетом условия (8), получаем:
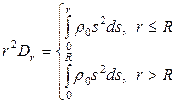, (10)
откуда
. (11)
Легко видеть, что функция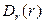 
удовлетворяет условию (7).
Далее,
. (12)
График 
постройте самостоятельно.
Нахождение 
.
Найдем из уравнения:
(13)
с граничными условиями:
А) 
(14)
(потенциал электростатического поля, создаваемого ограниченным в пространстве заряженным телом, естественно положить равным нулю на бесконечности);
Б) 
(15)
(непрерывность потенциала электростатического поля, создаваемого заряженным по объему телом).
Используя (12), получаем:
.
Нетрудно видеть, что условие (14) выполняется. Константу 
найдем из условия (15). Будем иметь:
. (16)
Примерный график функции постройте самостоятельно.
Замечание 1. Возможно, для нахождения потенциала проще воспользоваться формулой
.
Замечание 2. Дано подробное решение. На экзамене, в курсовой работе пишите кратко. Решение займет несколько строк. Возможно, будет предложена лишь часть задания.
Ш2. Металлический шар радиуса 
имеет заряд 
. Шар окружен концентрическим металлическим шаровым слоем с внутренним радиусом 
и внешним радиусом 
. Заряд слоя 
.
Где и как распределен заряд?
Найти напряженность электростатического поля, пользуясь теоремой Гаусса. Построить график ненулевой компоненты напряженности. Считать, что среда – вакуум.
Решение.
Введем сферические координаты 
.
В силу сферической симметрии задачи
. (1)
Теорема Гаусса. Рассмотрим вспомогательную Гауссову поверхность в виде сферы 
переменного радиуса 
. Для данной задачи теорема Гаусса имеет вид (почему?):
(2)
Здесь 
- заряд внутри поверхности .
Где и как распределен заряд. Шар и слой - проводники. Внутри проводника плотность свободных зарядов равна нулю. Заряд располагается на внешней поверхности шара, причем распределен равномерно с поверхностной плотностью 
.
Заряд шарового слоя располагается на двух внешних поверхностях слоя, которые мы условно обозначим как поверхности 
. Чтобы определить плотность заряда на каждой из поверхностей, используем электростатическую теорему Гаусса (2). Пусть 
. Ясно, что
= + 
. (3)
Так как напряженность поля внутри проводящего слоя равна нулю, то в силу (2)
,
откуда
= 
. (4)
Заряд на поверхности 
распределен равномерно с поверхностной плотностью 
.
На поверхности 
распределен заряд 
(так как суммарный заряд слоя равен 
); распределен равномерно с поверхностной плотностью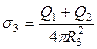 
.
Нахождение напряженности поля. Вновь обратимся к теореме Гаусса (2). Нетрудно убедиться, что в силу сферической симметрии поля соотношение (2) преобразуется к виду:
, (5)
откуда
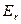
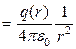. (6)
В силу сказанного ранее
. (7)
Из (6) и (7) ответ очевиден. График постройте самостоятельно.
О1. Отрезок 
оси 
равномерно заряжен и имеет заряд 
. Найдите потенциал 
поля, создаваемого заряженным отрезком в точках оси 
(вне отрезка).
Решение. Линейная плотность заряда отрезка: 
.
.
.
ПП1. Заряд распределен на плоскости 
(
) с поверхностной плотностью 
и на плоскости 
(
) с поверхностной плотностью 
. (Здесь 
- положительное число). В пространстве между плоскостями – среда с относительной диэлектрической проницаемостью 
, в остальных точках – вакуум.
1) Найдите индукцию 
и напряженность 
электрического поля. Воспользуйтесь уравнением Максвелла.
2) Изобразите график ненулевой компоненты напряженности для случая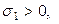 
.
3) Проверьте выполнение граничного условия для нормальных компонент вектора на заряженной поверхности
4) Не находя потенциала 
, постройте эскиз графика потенциальной функции при условии
. (1)
Решение
1). Ясно:
а) 
(*)
б) 
(2)
в) 
; 
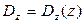(3)
Воспользуемся принципом суперпозиции.
, (4)
где векторы электрической индукции 
и 
характеризуют электрические поля, порождаемые зарядами на плоскостях и 
соответственно.
Каждый из векторов удовлетворяет уравнению Максвелла:
, (5)
где 
- обобщенная объемная плотность заряда. В каждом из случаев задача сводится к одномерной, поэтому будем считать, что 
. (См. подробнее задачу П1).
Тогда ясно, что
. (6)
С учетом (*), (2) и (3) уравнения (5) с правыми частями (6) запишутся в виде:
(7)
(8)
Понятно, что для каждой плоскости имеет место антисимметрия поля:
, (9)
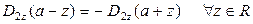. (10)
Решая уравнения (7), (8) получаем:
, 
(11)
Подобрав константы 
и 
с учетом (9) и (10), имеем:
, (12)
. (13)
(Подробнее см. решение задачи П1.)
. (14)
. (15)
2). График функции 
постройте самостоятельно.
3). Граничное условие для нормальных компонент напряженности на поверхности :
(16)
Индексами «+» и «-» помечены граничные значения нормальной компоненты вектора напряженности и относительной диэлектрической проницаемости соответственно на положительной и отрицательной сторонах поверхности . (Считаем, что положительная нормаль к этой плоскости задается ортом 
).
Для рассматриваемой задачи соотношение (16) принимает вид:
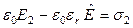. (17)
Проверить (17) нетрудно. В силу (15) соотношение (17) действительно имеет место.
4). Эскиз графика функции 
постройте самостоятельно. Примите во внимание следующие моменты.
(18)
Следовательно, если на некотором промежутке 
, то на этом промежутке возрастает; если на некотором промежутке 
, то на этом промежутке убывает.
Если на некотором промежутке 
возрастает, то на этом промежутке функция выпукла вверх.
Если на некотором промежутке убывает, то на этом промежутке функция выпукла вниз.
Замечание. На экзамене будет предложена только часть задания.
Некоторые указания к решению задач по электростатике
1. Электростатические поля, создаваемые заряженными телами: шаром, сферой, шаровым слоем, бесконечным круглым цилиндром, бесконечной цилиндрической поверхностью, бесконечным цилиндрическим слоем, плоскостью, несколькими параллельными плоскостями, бесконечной плоской плитой, бесконечной нитью следует находить
А) используя теорему Гаусса (чаще всего)
Б) из уравнений Максвелла или Пуассона
Обычно в условии конкретно указано, какой способ выбрать.
Если в задаче требуется найти потенциал, но не указано, в какой точке потенциал следует положить равным нулю, то эту точку следует выбрать самостоятельно.
При этом, если заряженное тело ограничено в пространстве (шар и т.п.), то потенциал принято считать равным нулю на бесконечности.
Если заряженное тело не ограничено (нить, цилиндр, плоскость и т.п.), то потенциал полагают равным нулю в некоторой конечной точке (точках) пространства. (Подумайте, что получится, если в задачах данного типа положить потенциал равным нулю на бесконечности. Потенциал будет определен некорректно).
2. Поля, создаваемые заряженными кольцом, диском, отрезком, ограниченным цилиндром, ограниченной цилиндрической поверхностью следует находить интегрированием по источникам поля. (Заряженное тело рассматриваем как совокупность (континуум) точечных источников). Интегрируются компоненты напряженности или потенциал.
3. Если проводник заряжен, заряды распределяются на внешней поверхности проводника.
Внутри проводника плотность свободных зарядов равна нулю, равна нулю и напряженность электрического поля.
[1] Электростатический потенциал непрерывен при распределении заряда в объеме или на поверхности (простой слой).