Расчет статистик методом произведений

МОДЕЛИРОВАНИЕ ЭКОСИСТЕМ

журнал для практических работ

для студентов специальностей 250201 и 250203, 120302 заочной формы обучения.

 

 

Екатеринбург

2009 г.

ЛАБОРАТОРНАЯ РАБОТА N1

Тема: Группировка данных, составление вариационного ряда,
графическое представление

Таблица 1.1

Исходные данные

N п/п				N п/п

1.2 Составление вариационного ряда по изучаемому признаку – _____:

Находим минимальную и максимальную величины____:

Xmax =; Xmin =;

Рассчитываем величину интервала С_ = =;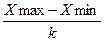

Количество классов берется 8÷12, обычно 10.

Более точный расчет производится по формуле k = 1+3,32*lg (N); где N – объем выборки;

Размах вариации L=Xmax – Xmin =

 

Группировка данных наблюдения

Таблица 1.2

Таблица построения вариационного ряда

Значения разрядов	Сводка данных	Частота (ni)	Накопленная частота Σni
действительные	центральные
Min
мax				∑
Сумма			∑

k=

Медиана Me =

 

Мода Mo =

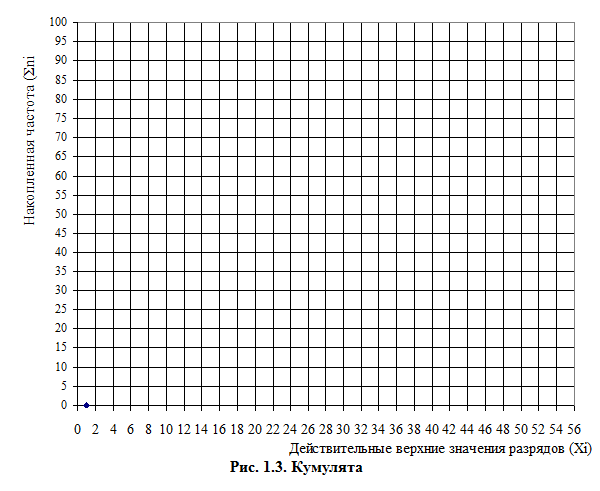
Графическое представление вариационного ряда

На рисунках 1.1-1.3 построить полигон частот, гистограмму и кумуляту.
На графике полигона частот нанести среднее значение и моду.

На графике кумуляты нанести медиану.

1.5. Составление вариационного ряда по изучаемому признаку – _H___:

Находим минимальную и максимальную величины____:

Xmax =; Xmin =;

Рассчитываем величину интервала С_ = =;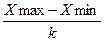

 

 

Группировка данных наблюдения

Таблица 1.3

Таблица построения вариационного ряда

Значения разрядов	Сводка данных	Частота (ni)	Накопленная частота Σni
действительные	центральные
Min
мax				∑
Сумма			∑

k=

1.6. Составление вариационного ряда по изучаемому признаку – _V____:

Находим минимальную и максимальную величины____:

Xmax =; Xmin =;

Рассчитываем величину интервала С_ = =;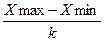

Размах вариации L=Xmax – Xmin =

 

Группировка данных наблюдения

Таблица 1.2

Таблица построения вариационного ряда

Значения разрядов	Сводка данных	Частота (ni)	Накопленная частота Σni
действительные	центральные
Min
мax				∑
Сумма			∑

k=

1.7. Задание по работе в Statgraphics Plus под Windows:

· изучить интерфейс статистико-графической программы Statgraphics Plus;

· импортировать индивидуальные данные из MS Office Ecxel в систему Statgraphics Plus;

· сохранить файл с данными;

 

Выводы:

 

ЛАБОРАТОРНАЯ РАБОТА N2

Тема: Статистики и параметры распределения

2.1. Вычисление статистик различными способами:

Таблица 2.1

Расчет статистик методом произведений

Середины классов (центральные значения) Xi	Частоты ni	Xi *ni	Xi2	Xi2 * ni
	Σ	Σ		Σ

Среднее арифметическое:

= =

Дисперсия:

D =

Среднеквадратическое отклонение:

σ = =

 

Коэффициент вариации:

 

СV= 100%=

Таблица 2.2

Расчет статистик методом условной средней

A (центральное значение класса, имеющий наибольшую частоту) =

Середины классов (центральные значения классов) Xi	Частоты ni	Отклонения Ai=Xi -А	Ai*ni	Ai 2* ni
Σ			Σ	Σ

Среднее значение:

= A+ =

Дисперсия:

D = =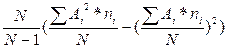

 

Среднеквадратическое отклонение:

σ = =

 

Коэффициент вариации:

 

CV= 100%=

Вычисление начальных моментов

Таблица 2.3

Определение сумм произведений условных произвольных отклонений различной степени на частоту классов

A (центральное значение класса, имеющий наибольшую частоту) =

РасчетA_i = ; - неименованная величина

Середины классов (центральные значения) Xi	Частоты ni	Условные произвольные отклонения
Ai	Aini	Ai2ni	Ai3ni	Ai4ni	(Ai+1)	(Ai+1)4ni
	Σ=		Σ=	Σ=	Σ=	Σ=		Σ=

Система начальных моментов:
(моменты вычисляются с точностью до 0,001):

m₁= =

m₂= =

m₃= =

m₄= =

Проверка:

1. m₄^*= =

2. m₄^* = 4m₁+ 6m₂+4m₃ +m₄+1 =

Система центральных моментов:

1;

0;

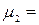m₂ – m₁²=

m₃ – 3m₂ m₁+ 2m₁³=

m₄–4 m₁m₃+ 6 m₁²m₂–3m₁⁴=

D =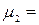

= =

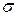Для перехода к именованным величинам необходимо значения дисперсии D и среднеквадратического отклонения домножить на величину интервала Cx:

_р= С_x² *

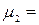
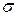_р= = =

 

Система основных моментов:

(в расчетах используем неименованные величины)

3= =

4= =

Среднее арифметическое:

=A+m₁C_х =

Коэффициент асимметрии (оценить результат):

S_k= =

Коэффициент эксцесса (оценить результат):

E = =

Основные ошибки статистик изучаемой величины ____:

(в расчетах используем именованные величины)

Ошибка среднего m = =

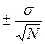Ошибка среднеквадратического отклонения m = =

Ошибка коэффициента вариации m_cv = ± =

Ошибка коэффициента асимметрии m_Sk = ±

Ошибка коэффициента эксцесса m_Se = ± 2* m_Sk

Точность опыта P = *100%=

Таблица 2.4

2.4.Сводная ведомость статистик по всем показателям:

Наименование статистики	Показатели
D, см	H, м	V, м3
2.4.1. Статистики ряда расположения:
среднее арифметическое ()
мода ()
медиана ()
2.4.2. Статистики изменчивости
дисперсия ()
среднеквадратичное отклонение ()
коэффициент вариации ()
размах вариации ()
2.4.3. Статистики отклонения ряда распределения от симметричного
коэффициент асимметрии ()
коэффициент эксцесса ()
2.4.4.Основные ошибки статистик
ошибка среднего ()
ошибка среднеквадратичного отклонения ()

Продолжение табл. 2.4

ошибка коэффициента вариации ()
ошибка коэффициента асимметрии ()
ошибка коэффициента эксцесса ()
точность опыта ()

 

2.5. Задание по работе в Statgraphics Plus под Windows:

· провести анализ одной переменной по диаметру (D), высоте - (H), объему -(V) (графический и табличный): получить основные статистики и графики рядов распределений, заполнить таблицу 2.4;

· сохранить статистический анализ в файле;

· распечатать полученные результаты (по указанию преподавателя);

· провести сравнительный анализ полученных данных.

Выводы:

ЛАБОРАТОРНАЯ РАБОТА N3