В задании №1 необходимо ответить письменно на теоретический вопрос. Материал можно использовать из учебных пособий на диске или на сайте филиала.
В задании №2 необходимо упростить выражение и доказать правильность упрощения при помощи таблицы истинности. Упрощение осуществляется, используя основные логические законы:
Коммутативные:
x 1 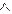 x 2 = x 2
x 2 = x 2 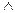 x 1, x 1
x 1, x 1 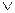 x 2 =x 2
x 2 =x 2 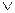 x 1;
x 1;
Дистрибутивные:
x 1 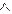 (x 2
(x 2 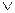 x 3) = (x 1
x 3) = (x 1 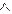 x 2)
x 2) 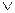 (x1
(x1 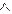 x3),
x3),
x1 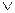 (x 2
(x 2 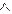 x3) = (x1
x3) = (x1 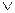 x 2)
x 2) 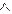 (x 1
(x 1 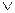 x 3);
x 3);
Ассоциативные:
x1 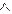 (x2
(x2 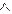 x 3) = (x1
x 3) = (x1 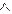 x 2)
x 2) 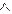 x3,
x3,
x1 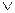 (x2
(x2 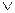 x 3) = (x1
x 3) = (x1 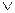 x 2)
x 2) 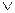 x 3;
x 3;
Законы Де Моргана:
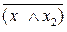 =
= 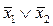 ,
, 
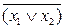 =
= 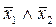 ,
,
Закон двойного отрицания:


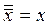 .
.
Кроме того, справедливы следующие соотношения:

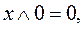
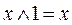 ,
, 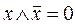 .
. 
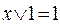 ,
, 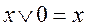 ,
, 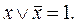
Сложные формулы, как правило, можно упростить. Для этого можно использовать следующие эквивалентности:
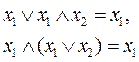 - правила поглощения;
- правила поглощения;
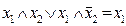 - правило склеивания;
- правило склеивания; 
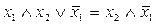 – правило вычеркивания.
– правило вычеркивания.
Их доказательства осуществляются путем построения соответствующих таблиц истинности.
При упрощении логического выражения необходимо учитывать приоритет выполнения логических операций:
- отрицание;
- логическое умножение 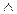 ;
;
- логическое сложение 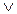 .
.
Рассмотрим пример упрощения логической функции. Пусть
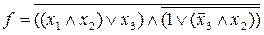
Последовательное применение приведенных выше правил дает:
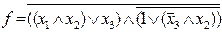 =
= 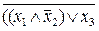
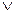

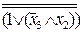 =
=
=(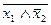
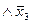 )
) 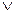
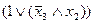 =(
=(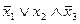 )
) 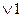 =1.
=1.
Докажем рассмотренное упрощение при помощи таблицы истинности:
Таблица 2.1 – Таблица истинности
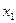
| 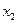
| 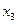
| 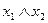
| 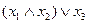 * *
| 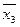
| 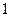
| 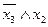
| 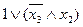
| 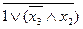 ** **
| 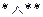
| 
|
Из таблицы истинности видно, что упрощение выполнено, верно.
В задании №3 необходимо в Маткаде составить программу вычисления и выдачи на печать суммы (или произведения) N элементов бесконечного числового ряда.
Пример №1. Вычислить сумму ряда y=1+6+11+16+21+…
Используя средства программирования Маткада, описанные в первой главе, составим программу:
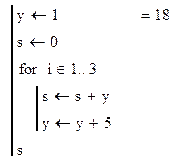
Пример №2. Вычислить сумму ряда y=-1+6-11+16-21+…
Используя средства программирования Маткада, описанные в первой главе, составим программу:
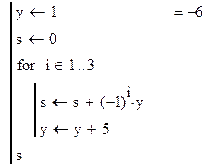
Пример №3. Вычислить сумму ряда
y=(1/2-2/5)+(3/3+4/10)+(5/4-8/15)+(7/5+16/20)-…
Используя средства программирования Маткада, описанные в первой главе, составим программу:
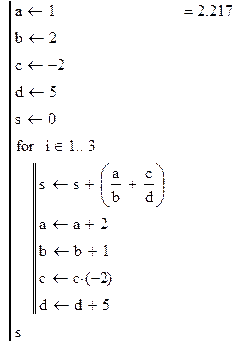
В задании №4 необходимо в Маткаде составить программу вычисления и выдачи на печать суммы (или произведения) N элементов бесконечного числового ряда.
Пример №1. Вычислить сумму всех нечетных положительных чисел. Например, если А={2,4,-3,0,5,1,6}, результат: 5+1=6.
Используя средства программирования Маткада, описанные в первой главе, составим программу:
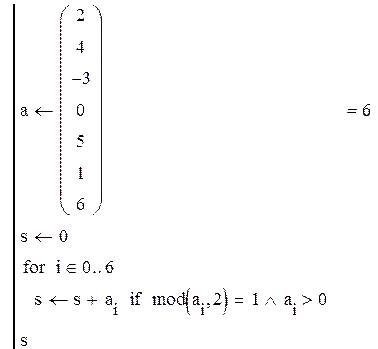
Пример №2. Вычислить среднеарифметическое значение всех положительных чисел. Например, если А={2,4,-3,0,5,1,6}, результат: 5+1=6.
Используя средства программирования Маткада, описанные в первой главе, составим программу:
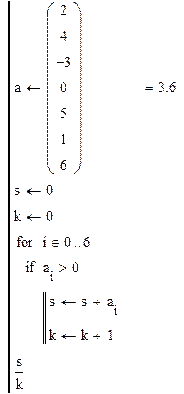
Задания к контрольной работе
Инструкция по выбору вариантов заданий: теоретический вопрос (задание №1) выбирается по ПОСЛЕДНЕЙ цифре шифра студента. Номера задач из заданий (№2-№4) выбираются по остатку от деления числа из двух последних цифр шифра на 33 (для шифров 00-32 выбираются такие же номера; для шифров 33-65 вариант получается вычитанием 33; для шифров 66-98 вариант получается вычитанием 66; для шифра 99 вариант 0)
Задание №1.
0. Причины появления производственных систем искусственного интеллекта.
1. Использование знаний, накопленных человечеством в системах искусственного интеллекта.
2. Цели создания систем искусственного интеллекта
3. Основные типы агентов.
4. Прямая цепочка рассуждений.
5. Обратная цепочка рассуждений.
6. Виды поиска целевых состояний.
7. Логика предикатов. Кванторы.
8. Основные операции алгебры логики
9. Нечеткая логика.
Задание №2.
Упростить выражение. Проверить результат с помощью таблицы истинности.
0. 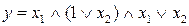
1. 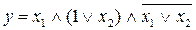
2. 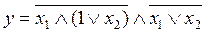
3. 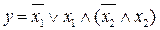
4. 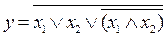
5. 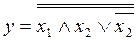
6. 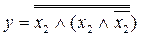
7. 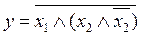
8. 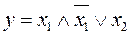
9. 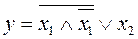
10. 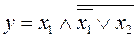
11. 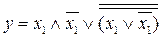
12. 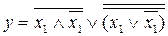
13. 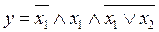
14. 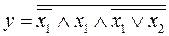
15. 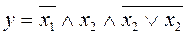
16. 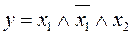
17. 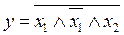
18. 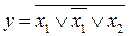
19. 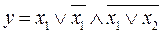
20. 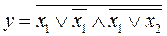
21. 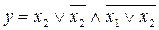
22. 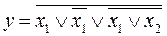
23. 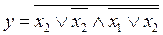
24. 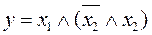
25. 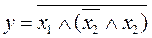
26. 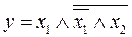
27. 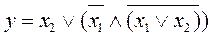
28. 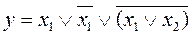
29. 
30. 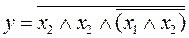
31. 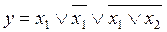
32. 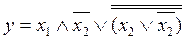
Задание №3.
Составить программу вычисления и выдачи на печать суммы (или произведения) N элементов бесконечного числового ряда.
0. y=1-6+11-16+21-…
1. y=-2+5-8+11-14+…
2. y=60-53+46-39+32…
3. y=-4+8-16+32-64…
4. y=16(-8)4(-2)1…
5. y=85-80+75-70+65-…
6. y=42-40+38-36+34-…
7. y=-20+15-10+5-0+…
8. y=3-9+27-81+243-…
9. y=70-65+60-55+50-…
10. y=125(-25)5(-1)0.2…
11. y=32(-16)8(-4)2…
12. y=1(-3)9(-27)81…
13. y=-18+20-22+24-…
14. y=(-3)6(-9)12(-15)…
15. y=(3+1-1/81)(5-2+1/27)(7+3-1/9)(9-4+1/3)…
16. y=(-2+1/80)(4-2/40)(-8+3/20)(16-4/10)…
17. y=-(20+1/1)+(18+2/3)-(16-3/5)+(14+4/)…
18. y=-(1/2-2/5)+(2/3+4/10)-(3/4-8/15)+(4/5+16/20)-…
19. y=-(3/16+1+2)+(3/8-2+4)-(3/4+3+6)+(3/2-4+8)-…
20. y=(2/16+8)(2/8-10)(2/4+12)(2/2-14)…
21. y=(2+1/81)-(4-2/27)+(8+4/9)-(16-8/3)…
22. y=(7+2/2)-(6-3/4)+(5+4/8)-(4-5/16)…
23. y=(-24)12(-6)3(-1.5)…
24. y=256(-64)16(-4)1…
25. y=4(-6)8(-10)12…
26. y=125(-25)5(-1)0.2…
27. y=(-10)8(-6)4(-2)…
28. y=(-1)4(-16)64(-256)…
29. y=-243+81-27+9…
30. y = 12 + 23 + 34 + 45...
31. y = 42 - 40 + 38 – 36...
32. y=4-6+8-10+12…
Задание №4.
Имеется массив А из N произвольных чисел - А(N), среди которых есть положительные, отрицательные и равные нулю. Составить программу, решающую задачу в соответствии с вариантом.
0. Вычислить сумму всех четных положительных чисел. Например, если А={2,4,-3,0,5,1,6}, результат: 2+4+6=12.
1. Вычислить количество чисел, квадрат которых меньше 10. Например, если А={2,4,-3,3,5,-2,1}, результат: 5 (это числа 2,-3,3,-2,1).
2. Вычислить количество нулевых чисел. Например, если А={2,4,-3,3,5,-2,1}, результат: нулевых – 0 (нет).
3. Ответить на вопрос: правда ли что среди чисел имеются отрицательные (ответ должен быть в виде слова «ДА» или «НЕТ»). Например, если А={2,4,-3,3,5,-2,1}, результат: ДА (-3,-2).
4. Напечатать все числа из очереди, квадрат которых превышает 7, но меньше 50. Например, если А={2,4,-3,3,5,-2,8}, результат: числа 4,-3,3,5.
5. Вычислить произведение всех положительных чисел меньше 20. Например, если А={2,24,-3,6,5,-2,33}, результат: 2*6*5=60.
6. Суммировать числа до тех пор, пока не встретиться число 2. Напечатать получившуюся сумму. Если двойка не встретилась, напечатать текст «ДВОЙКИ НЕТ». Например, если А={7,4,-3,2,5,-2,1}, результат 7+4-3=8.
7. Суммировать квадраты чисел до тех пор, пока сумма не превысит 40. Напечатать, на котором по счету числе это произошло. Например, если А={25,4,-3,3,5,-2,1}, результат 5 (сумма квадратов превысила 40 на пятом по счету числе 4+16+9+9+25=63).
8. Выяснить, каким по счету в очереди стоит число 3. если троек много, нас интересует только первая из них. Если троек нет совсем, напечатать «0». Например, если А={2,4,-3,3,5,-2,1}, результат: 4.
9. Подсчитать количество отрицательных чисел. Например, если А={2,4,-3,0,5,-2,5}, результат: 2.
10. Найти сумму и количество всех четных элементов. Например, если А={2,4,-3,0,5,-2,6}, результат: 12 и 4 (2,4,0,6).
11. Найти номер последнего отрицательного элемента в последовательности. Например, если А={2,4,-3,0,5,-2,5}, результат: 6 (число -2).
12. Напечатать только те числа из массива, которые образуют растущую последовательность. Например, если А={2,4,-3,4,2,-2,5}, результат 2,4 и -3,4 и -2,5.
13. Суммировать числа до достижения значения ≥15. Напечатать сумму и сделать ее =0. Опять продолжить суммирование до ≥15. Снова напечатать сумму и т.д. до конца массива. Если сумма оказалась меньше, печатать фразу «Сумма <15». Например, если А={8,6,4,3,5,12,5}, результат: 8+4+6=18 и 3+5+12=20 и 5.
14. Напечатать только те числа из массива, которые больше предыдущего числа. Например, если А={2,4,-3,0,5,7,5}, результат: 4 (4>2) и 0 (0>-3) и 5 (5>0) и 7 (7>5).
15. Напечатать те числа из массива, которые образуют убывающие последовательности. Например, если А={2,4,3,0,2,5,-2,5}, результат: 4,3,0 и 5,-2.
16. Складывать числа до встречи 0. Напечатать сумму. Снова суммировать до 0, напечатать новую сумму и т.д. до конца массива. Например, если А={2,4,0,-6,5,-2,0,7}, результат: 2+4=6 и -6+5-2=-3 и 7.
17. Найти сумму всех нечетных положительных чисел. Например, если А= {9,4,-3,0,5,1,-7}, результат: сумма =9+5+1=15
18. Найти максимальное и минимальное числа. Напечатать те элементы массива, которые в массиве находятся между ними. Например, если А={2,4,-3,0,2,5,-2}, результат: -3,0,2,5 (max=5, min=-3).
19. Найти номер последнего положительного элемента в массиве. Например, если А={2,4,-3,0,2,5,-2}, результат: 6 (последнее число 5).
20. Найти номера первых двух стоящих одинаковых элементов в массиве. Например, если А={2,6,4,4,2,5,5,4}, результат: 3 и 4 (одинаковые значения 4 и 4).
21. Выяснить, есть ли одинаковые элементы в массиве. Ответ 1-«да»/ 0-«нет». Например, если А={2,4,3,0,2,5,4}, результат: 1 (одинаковые значения 2 и 2).
22. Найти максимальный четный элемент в массиве. Например, если А={2,4,-3,6,2,9,-2}, результат: 6.
23. Найти произведение четных элементов, находящихся в диапазоне от 3 до 13. Например, если А={2,4,5,2,6,-2,20,8}, результат: 4*6*8.
24. Найти максимальное и минимальное нечетные числа и их среднее арифметическое. Например, если А={8,4,-2,6,2,7,-5}, результат: 7 и -5 и (7-5)/2=1.
25. Найти сумму элементов кратных трем. Например, если А={2,4,9,2,6,-12,0}, результат: 9+6-12=3.
26. Напечатать сумму элементов предшествующих максимальному числу. Например, если А={3,4,9,2,11,-12,3}, результат: 3+4+9+2=18.
27. Найти номер максимального четного элемента в массиве. Например, если А={2,4,-3,6,2,9,-2}, результат: 4.
28. Напечатать номера элементов кратных одновременно двум и трем. Например, если А={3,6,9,2,12,2,24}, результат: 6,12,24.
29. Напечатать произведение элементов следующих за минимальным числом. Например, если А={3,4,9,2,-5,2,3}, результат: 2*3.
30. Найти произведение элементов кратных трем. Например, если А={2,4,9,2,6,-3,0}, результат: 9*6*(-3)=-162.
31. Напечатать в обратном порядке все положительные элементы. Например, если А={2,4,-9,5,6,-3,2}, результат: 2,6,5,4,2.
32. Напечатать сумму элементов предшествующих минимальному числу. Например, если А={3,4,9,2,-5,2,3}, результат: 3+4+9+2=18.
Список литературы
1. Яньков В.Ю., Иглицкий А.М. Системы искусственного интеллекта..У чебно – практическое пособие пособие для студентов специальностей 210.200 и 220.200 всех форм обучения.Москва, 2006
2. Краснов А.Е., Красуля О.Н., Большаков О.В., Шлёнская Т.В. Информационные технологии пищевых производств в условиях неопределённости (системный анализ, управление и прогнозирование с элементами компьютерного моделирования). - М.: ВНИИМП, 2001. - 496 с.
3. Краснов А.Е., Красуля О.Н., Воробьёва А.В., Красников С.А., Кузнецова Ю.Г., Николаева СВ. Основы математического моделирования рецептурных смесей пищевой биотехнологии. - М.: Пище-промиздат, 2006. - 240 с.
4. Джордж Ф. Люггер. Искусственный интеллект. Стратегии и методы решения сложных проблем. Изд. «Вильямс»,2006
5. Стюарт Рассел, Питер Норрис. Искусственный интеллект. Современный подход. Издательство: «Вильямс», 2006 г.
6. Д. Рутковская, М. Пилиньский, Л. Рутковский. Нейронные сети, генетические алгоритмы и нечеткие системы. М., «Горячая линия – Телеком»,2007
Смирнов Денис Юрьевич
Яшин Денис Дмитриевич