МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ
ПО ВЫПОЛНЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ
НА ТЕМУ:
«РАСЧЕТ ЦИЛИНДРИЧЕСКОГО РЕДУКТОРА И ПОСТРОЕНИЕ ЗУБЧАТЫХ ЗАЦЕПЛЕНИЙ»
Содержание
Критерии выбора основных параметров
зубчатых передач………………………………………………………………2
2. Определение числа зубьев колес…………………………………………….3
3. Определение модуля зацепления…………………………………………..4
Определение степени точности цилиндрических
Зубчатых колес...................................................................................................5
Приложение 1……………………………………………………………………...6
1. Критерии выбора основных параметров зубчатых передач
В аппаратуре САУ, особенно в точных приборах, зубчатые передачи передают обычно небольшие крутящие моменты. Поэтому при конструировании зубчатых передач колеса, как правило, не рассчитывают, а выбирают их основные параметры, учитывая следующие соображения: конструкцию устройства, условия работы передачи, технологические особенности и возможности и др.
Кроме того, проводят проверочный расчет зубьев на прочность активных поверхностей и на изгибную прочность.
В общем случае расчет зубьев осуществляется по ГОСТ 21354-75. При проектировочном расчете зубчатых колес на изгибную прочность назначают материал колес и число зубьев и находят модуль. При расчете на поверхностную выносливость определяют межосевое расстояние a w и по нему находят модуль и число зубьев.
В сложных зубчатых передачах расчету зубьев на прочность предшествует кинематический расчет, заключающийся в выборе числа ступеней передачи и рациональном распределении общего передаточного отношения по ступеням.
При кинематическом расчете передаточных механизмов используют следующие основные критерии: минимизация размеров, массы, приведенного к входному валу момента инерции, погрешностей передачи.
При проектировании маломощного редуктора, исходя из:
1) критерия минимизации размеров, целесообразно колеса всех пар выполнить одного модуля и с одинаковым числом зубьев, т.е. z 1 = z 3 = z 5 = ... = z 2n-1, а передаточные числа всех пар принять равными, т.е.. u 1 = u 2 = u 3 = ... = u n.
В этом случае оптимальное число ступеней передачи n опт при заданном общем передаточном числе u р определяется зависимостью:
n опт = 1,85 lg u p
n__
а передаточное число каждой ступени u к = Ö u p
При проектировании редуктора, исходя из:
2) минимизации массы, принимают также:
z 1 = z 3 = ... = z 2n-1
n __
и u 1 = u 2 = ... = u n = Ö u p
Тогда оптимальное число ступеней редуктора определится выражением:
n опт = 3 lg u p,
При расчете числа ступеней редуктора следует учесть, что с его ростом падает К.П.Д. редуктора. Поэтому, округляя n опт до целого значения, необходимо брать ближайшее меньшее значение n опт.
3) точность редуктора возрастает с уменьшением числа ступеней в передаче.
Если принять, что максимально возможное передаточное число отдельной пары зубчатых колес u 1 = 8, то оптимальное число ступеней определится зависимостью:
n опт = 1,11 lg u p
На практике часто необходимо спроектировать зубчатую передачу с одновременным удовлетворением всех 3-х условий (минимизации размеров, массы, точности и др.). В этом случае число ступеней выбирают из условия минимизации размеров и разбивают общее передаточное отношение, принимая передаточное отношение тихоходной ступени максимально возможным.
2. Определение числа зубьев колес
После разбивки передаточного числа u p редуктора по ступеням приступают к определению числа зубьев каждой пары колес.
Рекомендуемое число зубьев меньшего колеса должно отвечать условию:
17 £ z 1 £ 28,
причем в точных отсчетных передачах желательно выбирать число зубьев ближе к верхнему пределу. Число зубьев большего колеса пары находят из соотношения:
z 2 = u 12 × z 1.
В силовых передачах число зубьев z 2 принимают не кратным z 1. Так, если передаточное число u 12 =4, число зубьев шестерни z 1 = 18, то число зубьев колеса должно быть 71 или 73, но не 72.
Для зубчатых передач применение колес с числом зубьев менее 12 не рекомендуется. В отсчетных передачах для повышения точности прибора число зубьев следует принимать равным или большим 25.
Рекомендуемые числа зубьев колес в зависимости от величины модуля:
Модуль Число зубьев
0,4; 0,5; 0,6 26 – 180
0,8 22 – 120
1,0 18 – 105
1,5 16 – 70
Не рекомендуется применять в приборах следующие числа зубьев: 101; 103; 107; 109; 127; 131; 149; 151; 157; 163; 173; 179; 181; 187; 191; 193; 197; 199; 202; 203; 206; 209; 211; 212; 214; 217; 221; 223; 227; 229; 233; 236; 239. Число зубьев свыше 240 рекомендуется принимать кратным 10.
3. Определение модуля зацепления
В зубчатых передачах аппаратуры САУ, как правило, основным видом разрушения зубьев является их поломка, вызванная многократным изгибом зуба. Для предотвращения поломок зубьев их рассчитывают на изгиб. При проектировочном расчете зубчатых колес на изгибную прочность назначают материал колес и число зубьев и определяют модуль зацепления.
Модуль для цилиндрического прямозубого колеса, мм, определяют по формуле:
3 __________________
m ³1,4Ö M K b U F / (z y вт [s] F ),
где М – крутящий момент на рассчитываемом колесе;
K b - коэффициент неравномерности нагрузки по ширине колеса, 1 ¸ 1,5;
(K b = 1 принимают при постоянной нагрузке, твердости зубьев НВ350 и окружной скорости v < 15 м/с);
U F = 4,8 ¸ 3,7 – коэффициент формы зуба (для числа зубьев от 17 до 200);
z – число зубьев шестерни;
y вт = b/m – коэффициент, равный отношению ширины b зубчатого венца к модулю; как правило, 3 £ y вт £ 16, причем меньшее значение выбирают для малогабаритных колес малой точности;
[s] F – допускаемое напряжение при расчете зубьев на изгиб, зависящее от прочностных характеристик материала колеса.
Допускаемое напряжение [s] F для симметричного цикла нагружения колеса определяют по формуле:
[s] F = s -1 / n з,
где s -1 - предел выносливости материала колеса, выбираемый из Т.У. на материал; n з –запас прочности.
Внимание!
В результате расчета зуба на изгиб могут получиться очень малые значения модуля. В этих случаях модуль следует назначить из конструктивных соображений и технологических возможностей производства зубчатых колес. При выборе модуля следует иметь в виду, что его увеличение приводит к росту размеров и массы передачи, а уменьшение модуля ниже 0,3 увеличивает погрешность передачи.
Определение степени точности цилиндрических зубчатых колес
Стандартом на зубчатые передачи с параллельными осями с металлическими, механически обработанными цилиндрическими прямозубыми колесами внешнего и внутреннего эвольвентного зацепления с углом профиля исходного контура 20° предусмотрены 7 степеней точности (4; 5; 6; 7; 8; 9 и 10) и следующие нормы:
а) нормы кинематической точности, регламентирующие погрешность передаточного отношения передачи и определяющие точность выходных величин механизма при работе его в одном направлении;
б) нормы плавности работы, регламентирующие циклические погрешности, многократно повторяющиеся за оборот колеса;
в) нормы контакта зубьев, определяющие полноту прилегания рабочих поверхностей зубьев колес в процессе работы передачи;
г) нормы боковых зазоров, определяющие в передачах с нерегулируемыми межцентровыми расстояниями при отсутствии зазоровыбирающих колес и компенсаторов величину мертвого хода передачи.
При изготовлении зубчатого колеса должно быть обеспечено выполнение требований всех 4-х групп норм точности.
В приложении I приведены нормы кинематической точности, нормы плавности работы, нормы контакта зубьев в передаче, наименьшие боковые зазоры, отклонения межцентрового расстояния и допуски на смещение исходного контура цилиндрических зубчатых колес.
При использовании приложения необходимо иметь в виду, что наибольшее применение в приборостроении имеют степени точности 6; 7 и 8-я.
Н а з н а ч е н и е с т е п е н и т о ч н о с т и ц и л и н д р и ч е с к и х з у б ч а т ы х к о л е с. 4-ю и 5-ю степени точности применяют для особо точных отсчетных зубчатых колес, к которым предъявляют особые требования в отношении постоянства передаточного отношения и плавности работы. Колеса 4-й и 5-й степеней точности изготовляют зубофрезерованием методом обката на особо точных станках с последующим шевингованием или полированием на высокоточных станках рабочих поверхностей зубьев.
6-ю степень точности применяют для высокоточных отсчетных зубчатых колес, для плавной бесшумной работы при малых мощностях и скоростях от 8 м/сек и более в приборах особо высокой чувствительности и точности, в прецизионных приборах и механизмах, в точных отсчетных передачах и измерительной аппаратуре. Колеса 6-й степени точности изготовляют зубофрезерованием методом обката на станках высокой точности с последующим шевингованием, шлифованием, притиркой и полированием поверхностей зубьев, а также холодным накатыванием.
7-ю степень точности применяют для точных зубчатых колес, для плавной работы при окружных скоростях до 8 м/сек в приборах управления и регулирования, в следящих системах радиолокационных устройств, гироскопических и других устройствах. Зубья колес изготовляют методом зубофрезерования и зубодолбления на точных станках, холодным накатыванием, волочением, протягиванием, с последующим для нарезанных колес шевингованием, шлифованием обкаткой, притиркой и приработкой рабочих поверхностей зубьев.
8-ю степень точности применяют для зубчатых колес средней точности и при окружных скоростях до 5 м/сек в рядовых передачах в приборах и агрегатах средней точности. Колеса допускают гудящий шум и биение без толчков. Зубья обрабатывают методом зубофрезерования и зубодолбления на станках средней точности с последующей обкаткой, притиркой и приработкой рабочих поверхностей зубьев.
9-ю степень точности применяют для зубчатых колес пониженной точности, предназначенных для работы в неотсчетных, неответственных передачах во всевозможных приборах и агрегатах, в которых зубчатые колеса служат для передачи вращения между осями. Колеса допускают сильный шум и удары в зубьях. Окружная скорость до 3 м/сек. Зубья колес обрабатывают методом деления, фрезерованием или долблением, а также обкатом на станках пониженной точности.
При контроле качества зубчатого колеса происходит проверка по нормам кинематической точности колеса, плавности работы колеса, контакта зубьев и боковых зазоров.
По нормам кинематической точности комплексным показателем является кинематическая погрешность колеса DFS - наибольшая погрешность угла поворота колеса в пределах одного оборота при однопрофильном зацеплении с точным колесом. При оценке качества зубчатого колеса по нормам кинематической точности, кинематическую погрешность колеса DFS равномерно заменяет накопленная погрешность окружного шага DtS.
При выборе степени точности следует исходить из конструктивного значения зубчатой передачи и условий ее эксплуатации. При этом необходимо учитывать заданную для данной передачи кинематическую погрешность (в угловых единицах или отсчетных делениях), предельные значения мертвого хода и крутящего момента, окружную скорость колес и другие требования, влияющие на точность.
При расчете точности зубчатой передачи, состоящей из нескольких пар цилиндрических колес, следует раздельно определять величину кинематической погрешности и величину мертвого хода для реверсивной передачи.
Величина кинематической погрешности передачи DFSпер в минуту определяется как сумма приведенных к ведомому валу кинематических погрешностей зубчатых колес:
i=n
DFSпер = hSDFSi,
i=1
где DFSi – кинематическая погрешность i- го зубчатого колеса в мк, равная
6,88DFSi
------------;
D д i
DFSi – кинематическая погрешность зубчатого колеса i в мк;
D д i – диаметр делительной окружности колеса в мм;
h- вероятностный коэффициент; рекомендуется принимать h = 0,7.
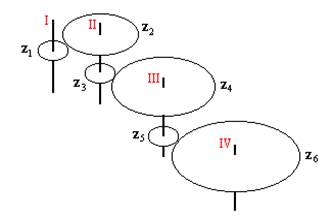 |
Рис. 1. К расчету кинематической погрешности передачи
П р и м е р. Рассчитать зубчатую передачу, приведенную на рис. 4:
Дано: z1 = 20; z2 = 40; z3 = 24; z4 = 60; z5 = 20; z6 = 80; m = 1; степень точности 7.
Величины кинематических погрешностей зубчатых колес согласно приложению 1 будут (в мк)
dFS1 = 40; dFS4 = 55;
dFS2 = 48; dFS5 = 40;
dFS3 = 44; dFS6 = 55.
Передаточные отношения между валами будут
z1·z3·z5 20·24·20 1
i I - IV = ---------- = ------------ = ----;
z2·z4·z6 40·60·80 20
z3·z5 24·20 1
i II - IV = ------- = ------------ = ----;
z4·z6 60·80 10
z5 20 1
i III - IV = ---- = ---- = ----.
z6 80 4
Подставив значения d и i в формулу, получим
dFSпер = 4,8 [40/20 · 1/20 + (48/40 + 44/24) · 1/10 + (56/60 +40/20) · ¼ + 55/80] = 8,73 мин.
Остальные параметры зуба и колеса тоже можно выразить через модуль:
1. Высота зуба, мм:
h = 2,2 m;
2. высота головки зуба, мм:
ha = m;
3. высота ножки зуба, равная h – ha, мм:
hf = 1,2 m;
4. расстояние между боковыми профилями зуба по начальной окружности (толщина
зуба), мм:
st = 0,5 pm;
5. шаг зацепления, т.е. расстояние между одноименными точками двух смежных зубьев, измеренное по начальной окружности, мм:
t = pm
6. диаметр начальной окружности(по ней происходит зацепление колес), мм:
dw = zm;
7. диаметр окружности выступов колеса, мм:
da = zm ± 2ha = zm ± 2m; (верхние знаки относятся к внешнему зацеплению);
8. диаметр окружности впадин колеса, мм:
df = zm ± 2hf = zm ± 2,4m; (нижние знаки относятся к внешнему зацеплению);
9. межцентровое расстояние, мм:
d w1 + d w2
a w = ----------------
По ГОСТ 9563-60 модули зубчатых зацеплений следует выбирать из следующего ряда:
0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1,0; 1,25;
1,5; 2,0; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40; 50; 60; 80; 100.
ПРИЛОЖЕНИЕ 1
Таблица 1 Нормы кинематической точности цилиндрических колес.
| Степень точности | Обознач. допуска | Модуль нормальный mn в мм | Размерность | Диаметр колеса в мм | ||||||
| До 12 | Св.12 до 20 | Св.20 до 30 | Св.30 до 50 | Св.50 до 80 | Св.80 до120 | Св.120 до 200 | ||||
| 4 – я | Допуск на кинематич. погрешность dFS | До 0,5 Св.0,5до 1 Св.1 до2,5 | мкм | |||||||
| 5 – я | До 0,5 Св.0,5до 1 Св.1 до2,5 | мкм | ||||||||
| 6 – я | До 0,5 Св.0,5до 1 Св.1 до2,5 | мкм | ||||||||
| 7 – я | До 0,5 Св.0,5до 1 | мкм | ||||||||
| 8 – я | До 0,5 Св.0,5до 1 | мкм | ||||||||
| 9 – я | До 0,5 Св.0,5до 1 | мкм |