Министерство образования и науки, молодежи и спорта Украины
Севастопольский национальный технический университет
«УТВЕРЖДАЮ»
Заведующий кафедрой технической кибернетики
д.т.н., профессор _________ Л.А. Краснодубец
«____»______________2011 г.
ФОНД КОНТРОЛЬНЫХ ЗАДАНИЙ ДЛЯ
ПРОВЕРКИ ОСТАТОЧНЫХ ЗНАНИЙ
По дисциплине
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
И ИССЛЕДОВАНИЕ ОПЕРАЦИЙ
Общий объем 72 часа (2 кредита).
Направление 0502 – Системная инженерия.
Специальность 7.050201 - Компьютеризированные системы управления и автоматика
Кафедра технической кибернетики
Разработал д.т.н., проф. кафедры Шушляпин Е.А.
Фонд заданий рассмотрен и утвержден на заседании кафедры технической кибернетики протокол № _____ от «____»______________200 _г.
Заведующий кафедрой технической кибернетики_____________________________
1. Дана постановка задачи:

К какому типу оптимизационных задач относится данная задача?
Варианты ответа: а) нелинейная задача математического программирования; б) линейная задача математического программирования; в) нелинейная задача оптимального управления; г) линейная задача оптимального управления; д) это не оптимизационная задача.
2. Дана постановка задачи:

К какому типу оптимизационных задач относится данная задача?
Варианты ответа: а) нелинейная задача математического программирования; б) линейная задача математического программирования; в) нелинейная задача оптимального управления; г) линейная задача оптимального управления; д) это не оптимизационная задача.
3. Дана постановка задачи:

К какому типу оптимизационных задач относится данная задача?
Варианты ответа: а) нелинейная задача математического программирования; б) линейная задача математического программирования; в) нелинейная задача оптимального управления; г) линейная задача оптимального управления; д) это не оптимизационная задача.
4. Дана постановка задачи:

К какому типу оптимизационных задач относится данная задача?
Варианты ответа: а) нелинейная задача математического программирования; б) линейная задача математического программирования; в) нелинейная задача оптимального управления; г) линейная задача оптимального управления; д) это не оптимизационная задача.
5. Дана постановка задачи:

К какому типу оптимизационных задач относится данная задача?
Варианты ответа: а) нелинейная задача математического программирования; б) линейная задача математического программирования; в) нелинейная задача оптимального управления; г) линейная задача оптимального управления; д) это не оптимизационная задача.
6. Дана постановка задачи математического программирования

К какому типу задач относится данная задача:
Варианты ответа: а) обычная задача линейного программирования; б) задача целочисленного линейного программирования; в) задача частично-целочисленного линейного программирования; г) обычная задача нелинейного программирования; д) задача целочисленного нелинейного программирования; е) задача частично-целочисленного нелинейного программирования; ж) это не задача математического программирования.
7. Дана постановка задачи математического программирования

К какому типу задач относится данная задача:
Варианты ответа: а) обычная задача линейного программирования; б) задача целочисленного линейного программирования; в) задача частично-целочисленного линейного программирования; г) обычная задача нелинейного программирования; д) задача целочисленного нелинейного программирования; е) задача частично-целочисленного нелинейного программирования; ж) это не задача математического программирования.
8. Дана постановка задачи математического программирования

К какому типу задач относится данная задача:
Варианты ответа: а) обычная задача линейного программирования; б) задача целочисленного линейного программирования; в) задача частично-целочисленного линейного программирования; г) обычная задача нелинейного программирования; д) задача целочисленного нелинейного программирования; е) задача частично-целочисленного нелинейного программирования; ж) это не задача математического программирования.
9. Дана постановка задачи математического программирования

К какому типу задач относится данная задача:
Варианты ответа: а) обычная задача линейного программирования; б) задача целочисленного линейного программирования; в) задача частично-целочисленного линейного программирования; г) обычная задача нелинейного программирования; д) задача целочисленного нелинейного программирования; е) задача частично-целочисленного нелинейного программирования; ж) это не задача математического программирования.
10. Дана постановка задачи математического программирования

К какому типу задач относится данная задача:
Варианты ответа: а) обычная задача линейного программирования; б) задача целочисленного линейного программирования; в) задача частично-целочисленного линейного программирования; г) обычная задача нелинейного программирования; д) задача целочисленного нелинейного программирования; е) задача частично-целочисленного нелинейного программирования; ж) это не задача математического программирования.
11. Дана постановка задачи математического программирования

К какому типу задач относится данная задача:
Варианты ответа: а) обычная задача линейного программирования; б) задача целочисленного линейного программирования; в) задача частично-целочисленного линейного программирования; г) обычная задача нелинейного программирования; д) задача целочисленного нелинейного программирования; е) задача частично-целочисленного нелинейного программирования; ж) это не задача математического программирования.
12. Дана постановка задачи математического программирования
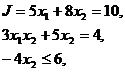
К какому типу задач относится данная задача:
Варианты ответа: а) обычная задача линейного программирования; б) задача целочисленного линейного программирования; в) задача частично-целочисленного линейного программирования; г) обычная задача нелинейного программирования; д) задача целочисленного нелинейного программирования; е) задача частично-целочисленного нелинейного программирования; ж) это не задача математического программирования.
13. Дана постановка многокритериальной задачи математического программирования и соответствующая однокритериальная задача со свернутым критерием:


Варианты ответа: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
14. Дана постановка многокритериальной задачи математического программирования и соответствующая однокритериальная задача со свернутым критерием:
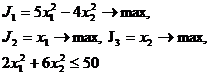

Варианты ответа: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
15. Дана постановка многокритериальной задачи математического программирования и соответствующая однокритериальная задача со свернутым критерием:


Варианты ответа: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
16. Дана постановка многокритериальной задачи математического программирования и соответствующая однокритериальная задача со свернутым критерием:


Варианты ответа: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
17. Дана постановка многокритериальной задачи математического программирования и соответствующая однокритериальная задача со свернутым критерием:


Варианты ответа: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
18. Дана постановка многокритериальной задачи математического программирования и соответствующая однокритериальная задача со свернутым критерием:


Варианты ответа: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
19. Дана постановка многокритериальной задачи математического программирования и соответствующая однокритериальная задача со свернутым критерием:


Варианты ответа: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
20. Дана постановка многокритериальной задачи математического программирования и соответствующая однокритериальная задача со свернутым критерием:


Варианты ответа: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
21. Указать форму задачи линейного программирования:

Варианты ответа: а) общая; б) стандартная; в) каноническая; г) каноническая с единичным базисом.
22. Указать форму задачи линейного программирования:

Варианты ответа: а) общая; б) стандартная; в) каноническая; г) каноническая с единичным базисом.
23. Указать форму задачи линейного программирования:

Варианты ответа: а) общая; б) стандартная; в) каноническая; г) каноническая с единичным базисом.
24. Указать форму задачи линейного программирования:

Варианты ответа: а) общая; б) стандартная; в) каноническая; г) каноническая с единичным базисом.
25. От задачи линейного программирования

перейти к ее канонической форме.
Варианты ответов:
а)  б)
б)  в)
в) 
г)  д)
д) 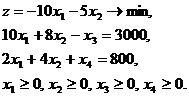
26. От задачи линейного программирования

перейти к ее канонической форме.
Варианты ответов:
а)  б)
б)  в)
в) 
г)  д)
д) 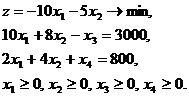
27. От задачи линейного программирования

перейти к ее канонической форме.
Варианты ответов:
а)  б)
б)  в)
в) 
г)  д)
д) 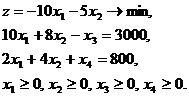
28. От задачи линейного программирования

перейти к ее канонической форме.
Варианты ответов:
а)  б)
б)  в)
в) 
г)  д)
д) 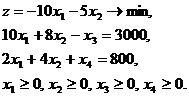
29. От задачи линейного программирования

перейти к ее канонической форме.
Варианты ответов:
а)  б)
б)  в)
в) 
г)  д)
д) 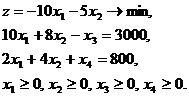
30. Дана задача линейного программирования в канонической форме:

Какое из перечисленных ниже решений является базисным решением, связанным с базисом 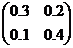 ?
?
Варианты ответа: а)  ; б)
; б)  в)
в)  .
.
31. Дана задача линейного программирования в канонической форме:

Какое из перечисленных ниже решений является базисным решением, связанным с базисом  ?
?
Варианты ответа: а)  ; б)
; б)  в)
в)  .
.
32. Дана задача линейного программирования в канонической форме:

Какое из перечисленных ниже решений является базисным решением, связанным с базисом  ?
?
Варианты ответа: а)  ; б)
; б)  в)
в)  .
.
33. Для симплекс-таблицы
| Свободные члены | х1 | х2 | х3 | |
| Коэффициенты критерия | -2 | -3 | ||
| х4 | ||||
| х5 | -2 |
определить возможные ведущие элементы.
Варианты ответа: а) x4-x1; б) x4-x2; в) x4-x3 г) x5-x1; д) x5-x2; е) x5-x3 (в вариантах ответов приведены обозначения строк и столбцов с предполагаемым ведущим элементом на их пересечении).
34. Для симплекс-таблицы
| Свободные члены | х1 | х2 | х3 | |
| Коэффициенты критерия | -2 | -3 | ||
| х4 | ||||
| х5 | -2 |
определить возможные ведущие элементы.
Варианты ответа: а) x4-x1; б) x4-x2; в) x4-x3 г) x5-x1; д) x5-x2; е) x5-x3 (в вариантах ответов приведены обозначения строк и столбцов с предполагаемым ведущим элементом на их пересечении).
35. Для симплекс-таблицы
| Свободные члены | х1 | х2 | х3 | |
| Коэффициенты критерия | -4 | -2 | ||
| х4 | ||||
| х5 | -2 |
определить возможные ведущие элементы.
Варианты ответа: а) x4-x1; б) x4-x2; в) x4-x3 г) x5-x1; д) x5-x2; е) x5-x3 (в вариантах ответов приведены обозначения строк и столбцов с предполагаемым ведущим элементом на их пересечении).
36. Для симплекс-таблицы
| Свободные члены | х1 | х2 | х3 | |
| Коэффициенты критерия | -4 | -3 | -2 | |
| х4 | -6 | |||
| х5 |
определить возможные ведущие элементы.
Варианты ответа: а) x4-x1; б) x4-x2; в) x4-x3 г) x5-x1; д) x5-x2; е) x5-x3 (в вариантах ответов приведены обозначения строк и столбцов с предполагаемым ведущим элементом на их пересечении).
37. Для симплекс-таблицы
| Свободные члены | х1 | х2 | х3 | |
| Коэффициенты критерия | -2 | -3 | ||
| х4 | ||||
| х5 | -2 |
с ведущим элементом на пересечении строк х4-х2 пересчитать элементы столбца свободных членов.
Варианты ответов: а) 7.333, 1.667, 2.667; б) 1.000, 2.000, -6.000; в) 1.667, 2.667, 3.667; г) 0.667, 0.333, -0.667.
38. Для симплекс-таблицы
| Свободные члены | х1 | х2 | х3 | |
| Коэффициенты критерия | -2 | -3 | ||
| х4 | ||||
| х5 | -2 |
с ведущим элементом на пересечении строк х5-х2 пересчитать элементы столбца х1.
Варианты ответов: а) 7.333, 1.667, 2.667; б) 1.000, 2.000, -6.000; в) 1.667, 2.667, 3.667; г) 0.667, 0.333, -0.667.
39. Для симплекс-таблицы
| Свободные члены | х1 | х2 | х3 | |
| Коэффициенты критерия | -2 | -3 | ||
| х4 | ||||
| х5 | -2 |
с ведущим элементом на пересечении строк х5-х2 пересчитать элементы столбца х2.
Варианты ответов: а) 7.333, 1.667, 2.667; б) 1.000, 2.000, -6.000; в) 1.667, 2.667, 3.667; г) 0.667, 0.333, -0.667.
40. Для симплекс-таблицы
| Свободные члены | х1 | х2 | х3 | |
| Коэффициенты критерия | -2 | -3 | ||
| х4 | ||||
| х5 | -2 |
с ведущим элементом на пересечении строк х5-х2 пересчитать элементы столбца х3.
Варианты ответов: а) 7.333, 1.667, 2.667; б) 1.000, 2.000, -6.000; в) 1.667, 2.667, 3.667; г) 0.667, 0.333, -0.667.
41. Для симплекс-таблицы
| Свободные члены | х1 | х2 | х3 | |
| Коэффициенты критерия | -2 | -3 | ||
| х4 | ||||
| х5 | -2 |
с ведущим элементом на пересечении строк х4-х3 пересчитать элементы столбца свободных членов.
Варианты ответов: 0.5, 0.167, 0.333; б) 6.5, 0.833, 7.667; в) -0.5, 0.5, 3.000; г) 3.000, 1.333, 11.667
42. Для симплекс-таблицы
| Свободные члены | х1 | х2 | х3 | |
| Коэффициенты критерия | -2 | -3 | ||
| х4 | ||||
| х5 | -2 |
с ведущим элементом на пересечении строк х4-х3 пересчитать элементы столбца х1.
Варианты ответов: 0.5, 0.167, 0.333; б) 6.5, 0.833, 7.667; в) -0.5, 0.5, 3.000; г) 3.000, 1.333, 11.667
43. Для симплекс-таблицы
| Свободные члены | х1 | х2 | х3 | |
| Коэффициенты критерия | -2 | -3 | ||
| х4 | ||||
| х5 | -2 |
с ведущим элементом на пересечении строк х4-х3 пересчитать элементы столбца х2.
Варианты ответов: 0.5, 0.167, 0.333; б) 6.5, 0.833, 7.667; в) -0.5, 0.5, 3.000; г) 3.000, 1.333, 11.667
44. Для симплекс-таблицы
| Свободные члены | х1 | х2 | х3 | |
| Коэффициенты критерия | -2 | -3 | ||
| х4 | ||||
| х5 | -2 |
с ведущим элементом на пересечении строк х4-х3 пересчитать элементы столбца х2.
Варианты ответов: 0.5, 0.167, 0.333; б) 6.5, 0.833, 7.667; в) -0.5, 0.5, 3.000; г) 3.000, 1.333, 11.667.
45. Для задачи нелинейного программирования без ограничений

и ее решения градиентным методом по рекуррентной формуле  ,
,  ,
,  найти вектор градиента
найти вектор градиента  (
( ) в точке
) в точке  и определить
и определить  .
.
Варианты ответов: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
46. Для задачи нелинейного программирования без ограничений

и ее решения градиентным методом по рекуррентной формуле  ,
,  ,
,  найти вектор градиента
найти вектор градиента  (
( ) в точке
) в точке  и определить
и определить  .
.
Варианты ответов: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
47. Для задачи нелинейного программирования без ограничений

и ее решения градиентным методом по рекуррентной формуле  ,
,  ,
,  найти вектор градиента
найти вектор градиента  (
( ) в точке
) в точке  и определить
и определить  .
.
Варианты ответов: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
48. Для задачи нелинейного программирования без ограничений

и ее решения градиентным методом по рекуррентной формуле  ,
,  ,
,  найти вектор градиента
найти вектор градиента  (
( ) в точке
) в точке  и определить
и определить  .
.
Варианты ответов: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
49. Для задачи нелинейного программирования без ограничений

и ее решения градиентным методом по рекуррентной формуле  ,
,  ,
,  найти вектор градиента
найти вектор градиента  (
( ) в точке
) в точке  и определить
и определить  .
.
Варианты ответов: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
50. Для задачи нелинейного программирования без ограничений

и ее решения методом Ньютона по рекуррентной формуле  ,
,  ,
,  найти вектор градиента
найти вектор градиента  (
( ) в точке
) в точке  , гессиан
, гессиан  , его обратную матрицу
, его обратную матрицу  , и определить
, и определить  .
.
Варианты ответов: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е) 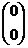 .
.
51. Для задачи нелинейного программирования без ограничений

и ее решения методом Ньютона по рекуррентной формуле  ,
,  ,
,  найти вектор градиента
найти вектор градиента  (
( ) в точке
) в точке  , гессиан
, гессиан  , его обратную матрицу
, его обратную матрицу  , и определить
, и определить  .
.
Варианты ответов: а)  ; б)
; б)  ; в)
; в) 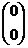 ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
52. Для задачи нелинейного программирования без ограничений

и ее решения методом Ньютона по рекуррентной формуле  ,
,  ,
,  найти вектор градиента
найти вектор градиента  (
( ) в точке
) в точке  , гессиан
, гессиан  , его обратную матрицу
, его обратную матрицу  , и определить
, и определить  .
.
Варианты ответов: а) 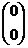 ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
53. Для задачи нелинейного программирования без ограничений

и ее решения методом Ньютона по рекуррентной формуле  ,
,  ,
,  найти вектор градиента
найти вектор градиента  (
( ) в точке
) в точке  , гессиан
, гессиан  , его обратную матрицу
, его обратную матрицу  , и определить
, и определить  .
.
Варианты ответов: а)  ; б)
; б)  ; в)
; в) 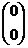 ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
54. Для задачи нелинейного программирования без ограничений

и ее решения методом Ньютона по рекуррентной формуле  ,
,  ,
,  найти вектор градиента
найти вектор градиента  (
( ) в точке
) в точке  , гессиан
, гессиан  , его обратную матрицу
, его обратную матрицу  , и определить
, и определить  .
.
Варианты ответов: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д) 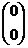 ; е)
; е)  .
.
55. Для задачи нелинейного программирования без ограничений

и ее решения методом Ньютона по рекуррентной формуле  ,
,  ,
,  найти вектор градиента
найти вектор градиента  (
( ) в точке
) в точке  , гессиан
, гессиан  , его обратную матрицу
, его обратную матрицу  , и определить
, и определить  .
.
Варианты ответов: а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 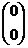 ; д)
; д)  ; е)
; е)  .
.
56. Задачу нелинейного программирования с ограничениями

свести к задаче без ограничений, используя штрафные функции типа «квадратичный штраф»  и «квадрат срезки»
и «квадрат срезки» 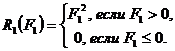 , где
, где  ограничение типа
ограничение типа  ,
,  ограничение типа
ограничение типа  .
.
Варианты ответов:
а) 
б) 
в) 
г) 
д) правильного ответа нет.
57. Задачу нелинейного программирования с ограничениями

свести к задаче без ограничений, используя штрафные функции типа «квадратичный штраф»  и «квадрат срезки»
и «квадрат срезки» 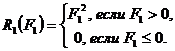 , где
, где  ограничение типа
ограничение типа  ,
,  ограничение типа
ограничение типа  .
.
Варианты ответов:
а) 
б) 
в) 
г) 
<