Задание рубежного контроля

Ожидаемой полезности

Проанализировав функцию полезности фон Неймана-Моргенштерна, рассмотрим, каким образом подход традиционной модели потребительского выбора может быть применен в случае такой функции.

Ожидаемая полезность может быть определена относительно любого числа исходов, наступающих с той или иной вероятностью. Допустим, что возможно наступление двух состояний – благоприятного и неблагоприятного. Индивидуум может получить обусловленные блага, т.е. блага, доступ к которым обусловлен наступлением одного или другого исхода с заданной вероятностью. Допустим, речь идет о получении различного дохода: в одном случае (благоприятном) - 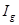, в другом (неблагоприятном) - .

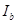Выбор в мире двух благ при отсутствии неопределенности сводится к решению задачи максимизации полезности при заданном бюджетном ограничении в рамках классической теории потребительского поведения. В условиях неопределенности индивид получит одно из обусловленных благ в зависимости от того, какая сложится ситуация – состояние. Но так как ему приходится выбирать, и возможно он получит некоторое количество каждого из возможных обусловленных благ, поскольку не знает, какой конкретно будет иметь место исход.

Будем считать, что функция полезности не зависит от наступления того или иного исхода и вероятность наступления благоприятного исхода равна 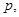то ожидаемая полезность получения обусловленных благ – двух разных уровней дохода составляет

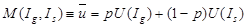(3.2.1)

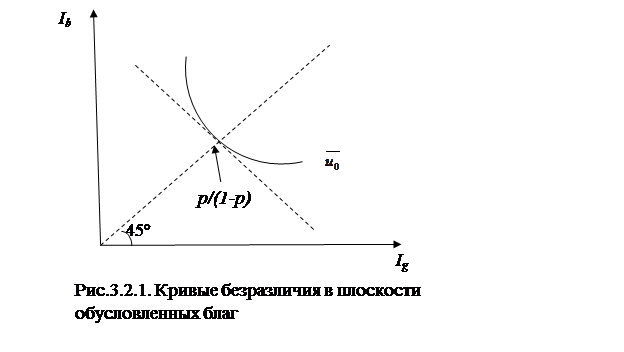
Эту величину индивид стремится максимизировать при заданном исходном уровне дохода. При таком выборе кривая безразличия представляет геометрическое место точек – комбинаций обусловленных благ, имеющих одинаковый уровень ожидаемой полезности 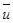для потребителя. На рис. 3.1. показана одна из таких кривых безразличия для уровня ожидаемой полезности .

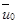На осях координат отложены количества обусловленных благ при благоприятном 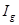и неблагоприятном 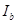исходах. Предельная норма замещения одного блага другим характеризует пропорцию, в которой индивид готов заменить доход (товар) при одном исходе, количество которого отложено по оси ординат, доходом (товаром), количество которого представлено на оси абсцисс при другом исходе. Предельная норма замещения измеряется соотношением предельных полезностей, и для функции (3.2.1) имеет вид:

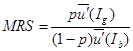. (3.2.2)

 

Поскольку функция ожидаемой полезности линейна по вероятностям исходов, то 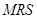равна произведению отношения вероятностей и отношения предельных полезностей. Но так как функция ожидаемой полезности одинакова для обоих исходов при равенстве дохода 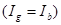вдоль луча – биссектрисы, выходящей из начала координат, то 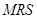равна отношению вероятностей наступления благоприятного и неблагоприятного исходов. Наклон кривой безразличия в точке 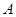зависит от величины вероятности благоприятного исхода 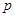. Если она велика, то кривая безразличия будет относительно крутой, и наоборот. Вдоль луча – биссектрисы все типы кривых безразличия индивида будут иметь одинаковый наклон.

Индивид, нейтрально относящийся к риску, не проводит различия между ожидаемой полезностью дохода и полезностью ожидаемой стоимости дохода, т.е. математическое ожидание 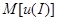(случайной) полезности дохода 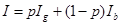в условиях риска равно полезности 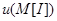математического ожидания случайного дохода, которое (математическое ожидание 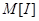) равно безрисковому доходу 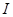, т.е. .

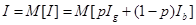По мере изменения 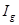и 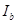при движении вдоль кривой безразличия предельная полезность дохода в каждом состоянии остается постоянной и, следовательно, отношение предельных полезностей не изменяется: 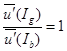. В соответствии с предельной нормой замещения (3.2.2) для индивида, нейтрального к риску, она равна постоянной величине - отношению вероятностей исходов 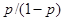. Такие кривые безразличия – прямые линии с наклоном, равным по абсолютной величине 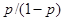, рис 3.2.2а.

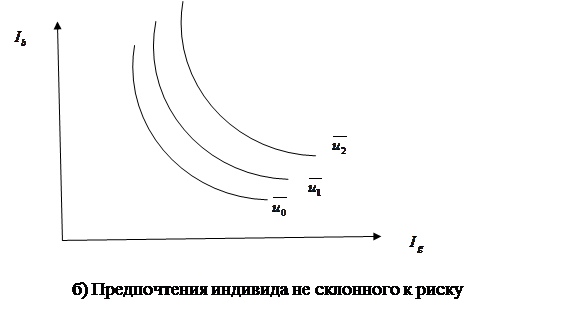
Предельная полезность дохода для индивида, не склонного к риску, убывает с ростом дохода и растет с его уменьшением, рис. 3.2.2б. При движении вдоль кривой безразличия в направлении увеличения 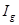и уменьшения 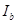предельная норма замещения снижается, что свидетельствует о выпуклости кривой безразличия относительно начала координат.

Для индивида, склонного к риску, предельная полезность дохода с его ростом увеличивается. Поэтому при движении вдоль кривой безразличия в направлении увеличения 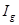и уменьшения 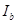предельная норма замещения растет. Такие кривые безразличия вогнуты относительно начала координат, рис. 3.2.2в.

Исходный уровень дохода, доступный и гарантированный, составляет 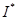. На рис. 3.2.3 такой доход отмечен точкой 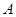на луче – биссектрисе. Поскольку в каждой точке на луче 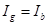, то его называют линией уверенности, т.е. линией дохода, которым индивид располагает наверняка. При движении вдоль этого луча вверх доход индивида растет в одинаковой пропорции при обоих исходах.

Рассмотрим все комбинаци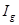и и 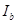, которые приносят индивиду ожидаемый доход 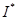, для которых 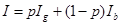. Выразим доход в случае неблагоприятного исхода 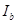через доход в случае благоприятного исхода 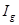, получим:

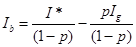. (3.2.3)

Это линия ожидаемого дохода с наклоном 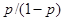, представляющая все варианты выбора с ожидаемой стоимостью дохода, равной исходному доходу индивида. Все варианты с ожидаемым доходом, например 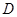и 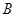, кроме варианта, отмеченного точкой 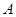, являются рисковыми, рис. 3.2.3.

Если индивид рискует и откажется от части дохода 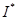и при этом выиграет 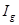в размере 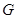. Индивид переместится в новую точку на бюджетной линии. Структура его дохода изменится: увеличится 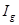на величину 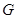и уменьшится 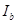на величину 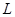. Индивид, выиграв исходный доход 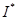, мог бы полностью обменять доход при неблагоприятном исходе на доход при благоприятном исходе. Пропорция этого обмена задана отношением вероятностей 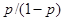. Выигрыш можно рассматривать как продажа доллара в неблагоприятных условиях и покупка их в благоприятных условиях по рыночным ценам 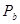и 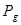. Тогда 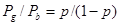. Индивид, проиграв и двигаясь от точки 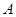в направлении точки 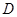, совершит обмен обратного рода по этим же ценам.

Таким образом, линия ожидаемого дохода аналогична бюджетной линии индивида с доходом 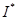и наклоном, равным отношению вероятностей и соотношению цен, так как цены условных благ равны соответствующим вероятностям: 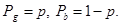Равенство цен вероятностям характеризует обмен благ индивидом как актуарно справедливую игру или игру со справедливыми исходами. Это имеет место в развитых рынках.

Параллельное перемещение бюджетной линии вправо означает увеличение дохода при обоих исходах. Изменение вероятности одного из исходов изменяет относительную цену, при которой индивид может обменять доход при одном исходе на доход при другом исходе. Норма замещения между обусловленными благами задана значениями цен или вероятностей.

Таким образом, модель выбора в условиях неопределенности полностью укладывается в рамки традиционной модели потребительского выбора.

Рассмотрим особенности оптимального положения индивида с различным отношением к риску. Если индивид не склонен к риску, то его кривые безразличия выпуклы относительно начала координат. Максимизация ожидаемой полезности достигается в точке касания кривой безразличия и бюджетной линии. Соблюдается условие

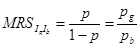(3.2.4)

на линии уверенности, и оптимум индивида не склонного к риску будет находиться в точке 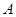пересечения линии уверенности и точки касания линии ожидаемого дохода и кривой безразличия, рис 3.2.4а.

 

Возникает вопрос, означает ли, что не склонный к риску индивид не заключает никаких договоров, например со страховой компанией. Если у экономического субъекта имеется первоначальный доход в точке 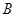, и он может заключить договор, который переместит его в точку 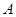, то он это сделает. Таким образом, речь идет о ситуациях изначально рискованных, и не склонный к риску индивид заключает договор со страховой компанией, перемещаясь в положение меньшего риска. Он максимизирует свою полезность, устраняя из своей жизни любой риск.

Если рынок обусловленных благ не удовлетворяет критерию справедливой игры и не выполняется условие (3.2.4), например , а , то бюджетная линия переместится из положения 1 в положение 2, рис. 3.2.5. Максимизация полезности будет достигаться не на линии уверенности, не в точке 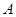, а в точке 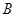под линией уверенности. Это означает, что индивид действует в направлении замещения в структуре своего доход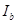а на 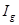, поскольку получение 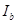обходится слишком дорого.

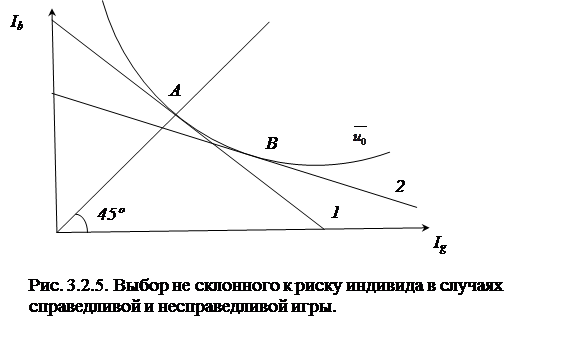
Субъекта не склонного к риску интересует величина ожидаемого дохода. Его кривые безразличия представляют прямые линии с наклоном 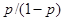, рис. 3.2.4б. Кривая безразличия лежит поверх бюджетной линии – линии ожидаемого дохода и для него представляет интерес любая точка на кривой безразличия (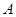, 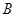или 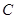), так как ожидаемый доход в них одинаков.

Для субъекта склонного к риску, рис 3.2.4.в, кривые безразличия характеризуются увеличивающейся предельной нормой замещения. Поэтому оптимум в таком случае возможен лишь в краевых точках. Если первоначальный доход отмечается точкой 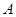, то самая большая полезность достигается в тоске 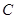, на оси абсцисс.

Заключение по разделу

Проанализировав особенности аксиом теории потребительского поведения с учетом вероятности получения предпочитаемого набора, определена сложная лотерея и сформулирована основная теорема теории ожидаемой полезности фон Неймана – Моргенштерна. Потребительский выбор рассмотрен с помощью модели ожидаемой полезности потребителя применительно к исходам, характеризующимся той или иной степенью неопределенности (случайности) с использованием теории полезности и теории вероятности. В качестве следствия теоремы о математическом ожидании полезности выведено правило рационального поведения потребителя в процессе принятия решения в условиях риска и неопределенности. Используя кривые безразличия в плоскости обусловленных благ в случаях предпочтений индивида нейтрального, склонного и несклонного к риску, проанализированы особенности оптимального положения индивида с различным отношением к риску.

Рассмотрено применение классического традиционного подхода модели потребительского выбора с применением функции полезности фон Неймана – Моргенштерна.

Проектное задание

Раскрыть особенности содержания аксиом теории потребительского поведения с учетом вероятности получения индивидом предпочитаемого набора. Определить содержание сложной лотереи и сформулировать основную теорему теории полезности фон Неймана – Моргенштерна. Обосновать правило рационального поведения в процессе принятия решений в условиях риска как следствие теоремы о математическом ожидании полезности.

Используя инструментарий традиционной теории потребительского поведения (кривые безразличия, предельную норму замещения благ, бюджетную линию и др.), проиллюстрировать графически и аналитически их особенности для индивидов с различным отношением к риску. Охарактеризовать особенности максимизации ожидаемой полезности индивидами с различным отношением к риску.

Контрольные вопросы

1. Как формулируется аксиома монотонности для предпочтения потребителя с учетом вероятности получить предпочитаемый набор?

2. В чем состоит особенность аксиомы непрерывности, на которую опирается функция ожидаемой полезности фон Неймана - Моргенштерна?

3. Объясните, почему присутствие третьего набора не нарушает предпочтения потребителя (аксиома о независимости).

4. Определите экономическое содержание сложной лотереи.

5. Сформулируйте основную теорему теории полезности фон Неймана – Моргенштерна.

6. В чем состоит отличие функции полезности фон Неймана-Моргенштерна и функции полезности, применяемой в традиционной теории потребительского выбора?

7. Представьте аналитически из определения полезность лотереи как математическое ожидание ее полезности.

8. Сформулируйте следствие теоремы о математическом ожидании полезности в виде правила рационального поведения индивида в процессе принятия решения в условиях риска.

9. Поясните экономический смысл элементов матрицы полезностей. Почему она выступает в качестве платежной матрицы?

10. Что собой представляет кривая безразличия для уровня ожидаемой полезности?

11. Определите предельную норму замещения обусловленных благ для функции ожидаемой полезности.

12. Сравните предельную норму замещения в традиционной теории потребительского поведения и в теории ожидаемой полезности фон Неймана-Моргенштерна.

13. Каково соотношение между ожидаемой полезностью дохода и полезностью ожидаемой стоимости дохода для индивида, нейтрально относящегося к риску?

14. Объясните, как и почему различаются кривые безразличия для индивида с различным отношением к риску?

15. Что собой представляет линия ожидаемого дохода?

16. Как выглядит на плоскости бюджетная линия при выборе потребителем обусловленных благ?

17. Чему равен наклон бюджетной линии при выборе в плоскости обусловленных благ?

18. Какова связь между ценами условных благ и вероятностями исходов?

19. Что собой представляет линия уверенности индивида?

20. Определите координаты точки, в которой достигается максимум ожидаемой полезности.

21. Охарактеризуйте особенности оптимального выбора индивида с различным отношением к риску.

22. Представьте графически выбор не склонного к риску индивида в случаях справедливой и несправедливой игры.

Задание рубежного контроля

1. Доказать, что отношения безразличия (̴) и строгого предпочтения (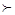), определенных соотношениями ( ̴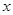 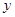, если и только ес л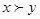и 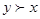и ) и 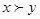, если и только если 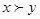, а отноше ние 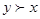несправедливо) справедливы следующие утверждения:

- отношение строгого предпочтения является транзитивным, рефлексивным и асимметричным;

- отношение безразличия является транзитивным и симметричным;

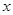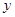- для двух заданных наборов и выполняется 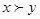, 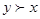или ̴ ;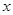

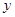- если функция полезности существует, то 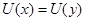, если и только если , в то время как , если и только если .

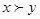2. Рассмотрим лексикографические предпочтения. Что является для них множеством безразличия? Показать, что для них не справедлива аксиома непрерывности.

3. Показать, что аксиома непрерывности эквивалентна допущению, что если 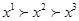, то любая непрерывная кривая, содержащая и 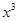, проходит через набор , такой, что ̴ .

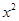4. Показать, что необходимые условия

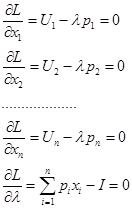
инвариантны по отношению к монотонному строгому возрастающему преобразованию полезности.

5. Имеются два товара, которые потребляются в установленных пропорциях:

- на плоскости этих товаров показать, как выглядят кривые безразличия и индивидуальный спрос;

- запишите алгебраически необходимые условия для равновесия потребителя.

6. Функция полезности является аддитивной, если .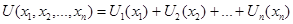

Какие ограничения на слабое отношение предпочт ени я 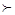гарантирует аддитивность функции полезности?

Показать, что если функция полезности аддитивна, то спрос на каждый товар зависит только от цены этого товара, цены любого другого товара и общего расхода на эти два товара.

Показать, что если функция полезности аддитивна, то в экономике не будет малоценных и взаимодополняемых товаров.

Показать, что аддитивная функция полезности предполагает только монотонное строго возрастающее линейное преобразование полезности.

7. Определим функции спроса Торнквиста

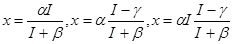
для «предметов первой необходимости», «предметов относительной роскоши» и «предметов роскоши» соответственно, где параметры 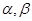и 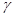зависят от цен.

Найти эластичности по доходу этих функций.

В случае двух товаров спрос на первый выражается функцией Торнквиста для «предметов первой необходимости» пр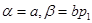и и 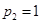(второй товар является единицей счета). Проверить, что соответствующая функция полезности имеет вид

.

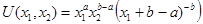8. Доказать, что если в пределах определенной группы товаров цены изменяются пропорционально, то такую группу можно рассматривать как один товар, который называется композитным (сложным). Достаточно рассмотреть три товара, причем цены двух из них всегда изменяются в одинаковой пропорции.

8. Товар Гиффена определяется тем, что спрос на него возрастает по мере повышения его цены. Покажите геометрически влияние дохода и влияние замены для товара Гиффена. Могут ли существовать товары Гиффена, если выполняется слабая аксиома выявленного предпочтения.

9. Так как функция полезности определена в пространстве всех наборов товаров, а функция спроса выражает оптимальный набор как функцию цен и дохода, то оптимальный уровень полезности косвенно зависит от цен и дохода.

Покажите, что косвенная функция полезности – убывающая функция всех цен и возрастающая функция дохода.

10. Используя аксиомы выявленного предпочтения, докажите

- существование функций спроса, т.е. что на самом деле любой набор цен и дохода приводит к выбору единственного набора товаров;

- однородность нулевой степени функций спроса.

11. Покажите, что для заданной шкалы полезности фон Неймана-Моргенштерна:

Монотонное строго возрастающее линейное преобразование полезности дает новую шкалу полезности, которая удовлетворяет аксиомам фон Неймана-Моргенштерна и выводам из них; монотонное строго возрастающее нелинейное преобразование полезности несовместимо с этими аксиомами и результатами.

На рис. 3.2.4 представлен графически выбор индивидов с различным отношением к риску в предположении, что вероятност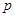и и 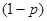, используемые для расчета наклона бюджетной линии, являются такими же, что и субъективные вероятности, используемые в определении ожидаемой функции полезности. Допустим, что, по мнению индивидов, субъективные вероятности отличны от объективных, определяющих цены условных благ, и составляют 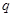и , где .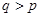

- Как изменятся кривые безразличия по сравнению с кривыми на рис. 3.2.4.

- Покажите, что произойдет с оптимумами индивидов в каждом из трех случаев.

Каждый набор обусловленных благ на линии уверенности характеризуется

- одинаковой степенью риска;

- одинаковым отношением вероятностей исходов;

- одинаковой ожидаемой стоимостью.

Для индивида, не склонного к риску, наклон кривой безразличия равен отношению вероятности исхода по оси абсцисс к вероятности исход по оси ординат:

- в каждой точке кривой безразличия;

- справа от набора начального запаса;

- слева от набора начального запаса;

- при пересечении кривой безразличия и линии уверенности.

Не склонный к риску индивид:

- будет играть в справедливую игру;

- не станет играть в справедливую игру;

- безразличен к тому, играть в справедливую игру или нет;

- не станет играть в несправедливую игру.

Литература

1.Гранатуров В.М. Экономический риск: сущность, методы измерения, пути снижения. М.: ДИС. 2002.

2. Кац М., Роузен Х. Микроэкономика. Мн.: Новое знание. 2004. Гл. 6.

3. Качалов Р.М. Управление хозяйственным риском. М.: Наука. 2002.

4. Лапуста М.Г., Поршнев А.Г., Старостин Ю.Л., Скамай Л.Г. Предпринимательство. М.: ИНФРА-М. 2006.

5. Нейман Дж. фон, Моргенштерн О. Теория игр и экономическое поведение. М.: Наука. 1970.

6. Трояновский В.М. Математическое моделирование в менеджменте. М. Русская деловая литература. 1999. Гл. 8-9, 11, 21.

7. Черемных Ю. Н. Микроэкономика. Продвинутый уровень. Учебник. М.: ИНФРА-М. 2008. Гл. 5.

8. Varian H. R. Microeconomic Analysis. W.W. Norton and Company. 1992.

9. Хэй Д., Моррис Д. Теория организации промышленности: В 2-х т. СПб.: экономическая школа. 1999. Т. 1. Т. 2.

10. Шоломицкий А.Г. Теория риска: Выбор при неопределенности и моделирование риска. М.: ГУ ВШЭ. 2005.