Глава 5. Магнитное поле в веществе
Намагниченность
Всякое вещество является магнетиком и способно под действием внешнего магнитного поля намагничиваться, т.е. приобретать магнитный момент. Тела, обладающие магнитным моментом, создают вокруг себя магнитное поле.
Если поместить проводник с током (током проводимости) в какую-нибудь среду (магнетик), то магнитное поле в любой точке среды будет являться суперпозицией полей
,
где 
индукция магнитного поля проводника с током (внешнее магнитное поле по отношению к магнетику); 
индукция магнитного поля намагниченного магнетика.
Выясним природу поля 
.
В молекулах вещества циркулируют молекулярные токи. Эти токи связаны с движением электронов в атомах и молекулах. Каждая такая молекула обладает магнитным моментом 
.
Суммарный магнитный момент всех молекул, в отсутствии внешнего магнитного поля, равен нулю (
), вследствие равновероятного направления магнитных моментов всех молекул.
Под действием внешнего магнитного поля 
, магнитные моменты молекул ориентируются по направлению этого поля, вследствие чего суммарный магнитный момент всех молекул становится отличным от нуля (
).
На примере показан магнит в отсутствии внешнего поля , случай а)
и в присутствии поля , случай б). (голубые стрелки)
Таким образом, в веществе возникает магнитное поле , которое влияет на результирующее поле 
.
Намагниченностью вещества называется величина
, (5.1)
где 
единичный объем; 
магнитный момент отдельной молекулы.
Намагниченность вакуума равна нулю, т.к. 
.
Поле , также, как и поле 
не имеет источников, поэтому
,
Это значит, что линии результирующего вектора 
и при наличии вещества остаются всюду замкнутыми.
Вектор 
возникает только при наличии молекулярных токов, то есть только в веществе.
Циркуляция вектора по замкнутому контуру 
, равна
, (5.2)
где 
суммарный молекулярный ток в магнетике.
В дифференциальной форме
, (5.3)
где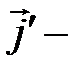 
плотность молекулярных токов в магнетике.
Напряженность магнитного поля
Так как в магнетиках существует не только ток проводимости, но и молекулярный ток, то теорема о циркуляции магнитной индукции в магнетиках
. (5.4)
полный ток,
где 
суммарный ток проводимости, 
суммарный молекулярный ток в магнетике, охватываемые контуром 
.
(5.4) – теорема о циркуляции вектора в магнетике в интегральной форме.
Используя теорему Стокса, можно показать, что
, (5.5)
где 
плотность тока проводимости; 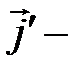плотность молекулярных токов.
(5.5) – теорема о циркуляции вектора в магнетике в дифференциальной форме.
Преобразуем (5.5) с учетом (5.3)
, (5.6)
или 
. (5.7)
Обозначим 
(5.8)
напряженность магнитного поля.
вспомогательный вектор, играющий существенную роль в магнетиках.
Из (5.8) и (5.7), видно, что
. (5.9)
(5.9) – теорема о циркуляции вектора 
в дифференциальной форме.
Используя теорему Стокса для вектора , получим
, (5.10)
где 
суммарный ток проводимости, охватываемый контуром 
.
(5.10) – теорема о циркуляции вектора 
в интегральной форме.
Связь намагниченности с напряженностью магнитного поля задается формулой
, (5.11)
где 
магнитная восприимчивость вещества.
Для изотропных (слабомагнитных) линейных магнетиков 
. Для нелинейных магнетиков 
. Для анизотропных сред 
тензор.
Размерность в СИ: 
.
Подставим (5.11) в (5.8), получим
, или
. (5.12)
Обозначим 
. (5.13)
магнитная проницаемость вещества.
С учетом (5.13) перепишем (5.12)
,
или
. (5.14)
(5.14) - связь между 
и 
для изотропных линейных магнетиков.
В вакууме 
, и совпадает по смыслу с (различаются коэффициентом 
).
В магнетиках напряженность играет роль «внешнего магнитного поля», а - поля в магнетике.
Намагниченность магнетиков 
не всегда совпадает по направлению с внешним магнитным полем 
. Это связано со структурой молекул магнетика. Все магнетики делятся на три больших класса: диамагнетики, парамагнетики и ферромагнетики.
5.3. Классификация магнетиков по магнитной восприимчивости 
1) диамагнетики 
( отрицательна, 
); 
(диамагнетики немного ослабляют внешнее магнитное поле).
Пример: водород, вода, висмут, серебро, золото (слабо выражены магнитные свойства);
2) парамагнетики 
( положительна, 
); 
(парамагнетики немного усиливают внешнее магнитное поле).
Пример: воздух, жидкий кислород, платина, алюминий (слабо выражены магнитные свойства)
3) ферромагнетики 
(нелинейные магнетики); (ферромагнетики во много раз усиливают внешнее магнитное поле).
Пример: железо, никель, кобальт (сильно выражены магнитные свойства).
Классификация по магнитной проницаемости 
: 
1) диамагнетики 
;
2) парамагнетики 
;
3) ферромагнетики 
.
Ферромагнетизм.
Кристаллические вещества, обладающие намагниченностью в отсутствии внешнего магнитного поля, называются ферромагнетиками.
Намагниченность ферромагнетиков в 
раз больше, чем намагниченность диамагнетиков и парамагнетиков.
Зависимость намагниченности ферромагнетиков от напряженности магнитного поля носит нелинейный характер, т.к. , и равна
. (5.15)
Это связано с особой доменной структурой ферромагнетиков.
Домены – (области 
) спонтанного намагничивания, т.е. области, намагниченные уже ранее каким-то внешним полем и сохраняющие свою ориентацию после его воздействия. В пределах каждого домена ферромагнетик намагничен до насыщения и имеет определенный магнитный момент. Направления магнитных моментов у различных доменов - различны.
Изменение или 
описывается петлей гистерезиса.
При 
. С ростом 
домены, ориентированные по полю, растут за счет доменов, ориентированных против поля. В слабых полях такой рост имеет обратимый характер, в сильных – необратимый. Это и служит причиной гистерезиса и остаточного намагничивания.
В состоянии магнитного насыщения (
) доменная структура ферромагнетика представляет собой единый домен, в котором все 
ориентированы по .
Уменьшая , домены начинают поворачиваться в обратном направлении и при 
, кривая пойдет через точку 
, характеризуя остаточную намагниченность вещества.
С наличием такого остаточного намагничивания связано существование постоянных магнитов.
Величина 
обращается в нуль (ферромагнетик размагничивается) лишь под действием поля 
, имеющего направление, противоположное полю, вызвавшему намагничивание. Величина называется коэрцитивной силой.
При увеличения противоположно направленного поля 
, ферромагнетик перемагничивается, достигая насыщения 
, затем его опять можно размагнитить.
При перемагничивании ферромагнетик нагревается. Площадь петли магнитного гистерезиса пропорциональна энергии, теряемой в образце за один цикл изменения 
, или энергии, идущей на перемагничивание ферромагнетика.
Значения 
и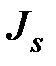 
для разных ферромагнетиков различно. Для трансформаторного железа петля гистерезиса узкая ( мало), для ферромагнетиков, используемых для изготовления постоянных магнитов, - широкая ( велико).
Для каждого ферромагнетика имеется предельная температура (точка Кюри 
), при которой он теряет свои особые ферромагнитные свойства (доменную структуру). При нагревании выше ферромагнетик становится обычным парамагнетиком. При охлаждении ферромагнетика ниже точки Кюри в нем снова возникают домены.
Для железа 
; для никеля 
.
Способы размагничивания ферромагнитных материалов: механический, температурный, электромагнитный.
5.5. Граничные условия для 
.
Поведение магнитного поля на границе раздела двух магнетиков устанавливается на основании двух теорем:
; (5.16)
. (5.17)
Из (5.16), а также с учетом того, что , следует
;
. (5.18)
Если на границе раздела нет токов проводимости, то 
, и
(5.19)
Из (5.18) и (5.19) следует, что при переходе через границу раздела двух магнетиков нормальная составляющая и тангенциальная составляющая 
изменяются непрерывно, а тангенциальная составляющая и нормальная составляющая претерпевают скачок.
На границе раздела двух магнетиков линии вектора и испытывают преломление
. (5.20)
(5.20) - закон преломления линий вектора 
.