Дисциплина: Математика
Группа 111з/т
Занятие 4
Тема урока: Первообразная и неопределённый интеграл
Цель урока:вспомнить 1) правила нахождение первообразной.
2)
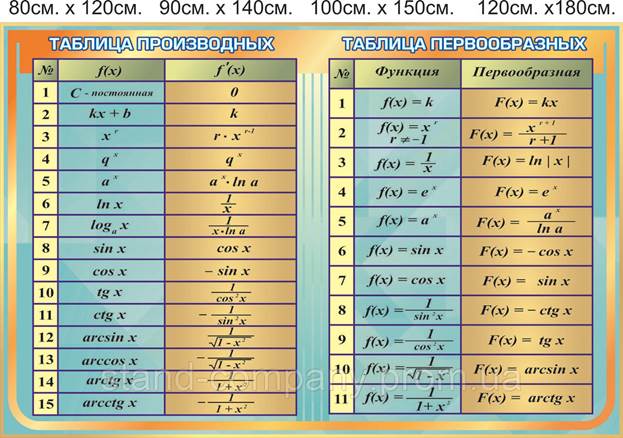
Первообразная. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке Х, если для х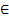 
Х выполняется равенство F’ (x) = f(x).
Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке Х, если для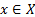 
выполняется равенство F’ (x) = f(x).
1) 
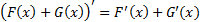
2) 
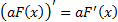
3) 
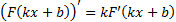
Примеры и разбор решения заданий тренировочного модуля
№1. Для функции y = f(x) найдите множество всех первообразных. Выполните проверку. f(x) = 2sin x + 3x3
Решение:
f(x) = 2sin x + 3x3
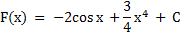
Проверка:
Найдем производную функции F(x).
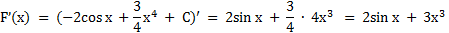
F’(x) = f(x)
Ответ: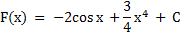
№2. Значение первообразной функции F(x) функции f(x) = 10cosx в точке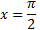 
равно -4. Найдите 
.
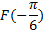Решение. Сначала найдем первообразную
F(x) = 10sinx+ C
Затем подставляя значения точки х, найдем число с
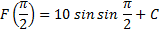
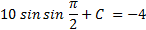
C = -14
Далее получаем уравнение первообразной в этой точке
F(x) = 10sin x – 14
И находим значение первообразной в другой точке
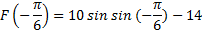
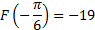
Ответ: -19
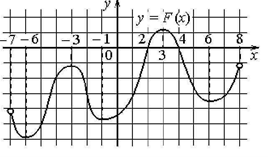
№3. По графику первообразной функции y = F(x) определите числовые промежутки, на которых функция y = f(x) имеет отрицательный знак.
Решение:
Так как F’(x) = f(x)- по определению первообразной, то числовые промежутки, на которых функция f(x) (производная функции F(x)) имеет отрицательный знак – это промежутки убывания функции F(x). Таких промежутков на данном графике 3. Это (-7; -6); (-3; -1); (3;6)
Ответ: (-7; -6); (-3; -1); (3;6)
№4. Значение первообразной функции F(x) функции f(x) = 5x3 – 3x2 + 7x – 2 в точке х = 0 равно 5. Найдите F(2).
Решение.
1. Найдем множество всех первообразных для данной функции.
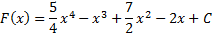
1. Так как в точке х = 0 значение первообразной функции равно 5, то нам необходимо найти такое значение С, для которого выполняется условие F(0) = 5.
Решим уравнение:
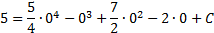
1. Из полученного уравнения находим С = 5.
Следовательно, первообразная для функции f(x) = 5x3 – 3x2 + 7x – 2 при заданном условии F(0) = 5 имеет вид: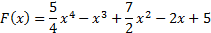 
1. Тогда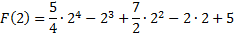 
F(2) = 27
Ответ: 27
Определение: множество всех первообразных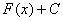 
для функции 
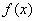называется неопределённым интегралом от функции 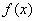и обозначается символом 
. Таким образом, по определению:
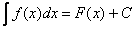, где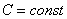 
Напоминаю, что функция 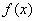называется подынтегральной функцией, 
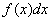– подынтегральным выражением, а сам процесс отыскания множества первообразных 
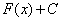– интегрированием. Интегрирование – это восстановление функции 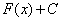по её производной 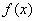(обратное действие по отношению к дифференцированию).
Для нашего демонстрационного примера:
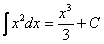, где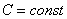
Проверка: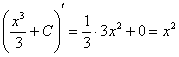 
– исходная подынтегральная функция.
Любая ли функция интегрируема? Нет.
Сформулируем достаточное условие интегрируемости: если на некотором промежутке функция непрерывна, то она интегрируема на нём.
Как видите, условие довольно-таки лояльное – для существования первообразной достаточно лишь непрерывности. Ниже по тексту, если не сказано иного, все функции будем считать интегрируемыми.
Свойства неопределённого интеграла
Нумеровать крайне не люблю, но здесь лучшего варианта не видно:
1) Производная от неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению:
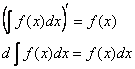
Доказательство: по определению неопределённого интеграла: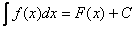 
, следовательно:
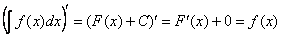, что и требовалось доказать.
Второе. По правилу раскрытия дифференциала (а точнее, по определению дифференциала) и только что доказанному пункту:
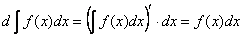
Потёрто.
2) Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
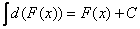
Учитывая, что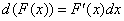 
, свойство можно переписать в следующем виде:
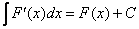
Тут даже доказывать ничего не надо, поскольку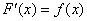 
и получается непосредственно само определение неопределённого интеграла.
Как видите, в обоих случаях значки дифференциала и интеграла взаимно уничтожаются, что естественно.
Следующие свойства вам хорошо знакомы – это мировые свойства линейности, которые справедливы и для других типов интегралов: определённых, двойных, тройных, криволинейных и пр.