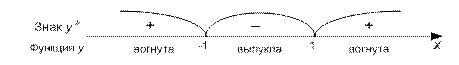Методические указания
К типовому расчету
«Исследование функций и построение графиков»
Приложение производной к исследованию функций
Монотонность функции
Определение. Функция y = f(x) возрастает (убывает) на промежутке Х, если " х 1, х 2Î Х: х 2> х 1 Þ f(х 2 ) > f(х 1 ) (f(х 2 ) < f(х 1 )).
Теорема 1. (необходимое условие монотонности). Если дифференцируемая на (a;b) функция y = f(x) возрастает (убывает),
то f ¢(x)≥0 (f ¢(x)≤0), " x Î(a;b).
Теорема 2. (достаточное условие монотонности). Если y = f(x) дифференцируема на (a;b) и " x Î(a;b): f ¢(x)>0 (f ¢(x)<0), то функция на (a;b) возрастает (убывает).
Экстремумы функции
Определение. Точка х 0 называется точкой локального max (min) функции y=f(x), если ∃ Оd(х 0): f(х 0 ) > f(х) (f(х 0 ) < f(х)), " x ÎОd(х 0).
Точки локального max (min) – это точки локального экстремума, а значения функции в этих точках - экстремумы функции.
Теорема 3. (необх. условие экстремума). Если дифференцируемая функция y=f(x) имеет в точке х 0 экстремум, то f ¢(х 0)=0 или f ¢(х 0) не существует. Обратное неверно.

 Т.о. непрерывная функция может иметь экстремум в точках, где f ¢(х)=0 или ∄ f ¢(х), т.е. в критических точках 1 рода.
Т.о. непрерывная функция может иметь экстремум в точках, где f ¢(х)=0 или ∄ f ¢(х), т.е. в критических точках 1 рода.
Теорема 4. (первое достаточное условие экстремума). Если непрерывная функция y=f(x) дифференцируема в некоторой окрестности точки х 0 и при переходе через нее f ¢ меняет знак с «+» на «-» (с «-» на «+»), то х 0 – точка max (min).
Теорема 5. (второй достаточный признак экстремума). Если функция y=f(x) дважды дифференцируема в некоторой окрестности точки х 0 и выполняются условия, то
1. 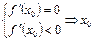 - точка max 2.
- точка max 2. 
 - точка min.
- точка min.
Замечание. Если f ¢¢(х 0)=0 или f ¢(х 0) не существует, то второй признак неприменим. Также признак неудобен при громоздкой форме f ¢¢(х).
Правило исследования y=f(x) на монотонность и экстремумы
1. Найти Df.
2. Вычислить f ¢(х) и найти критические точки 1 рода (f ¢(х)=0 или ∄ f ¢(х)).
3. Определить знак f ¢(х) в промежутках, на которые критические точки делят Df (определить промежутки знакопостоянства функции
y=f ¢(х)).
4. Найти интервалы возрастания и убывания функции, точки экстремума. Вычислить экстремумы функции.
Выпуклость графика функции. Точки перегиба
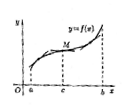 Определение. График функции называется выпуклым (вогнутыми) на интервале (a;b), если он расположен ниже (выше) любой ее касательной на этом интервале.
Определение. График функции называется выпуклым (вогнутыми) на интервале (a;b), если он расположен ниже (выше) любой ее касательной на этом интервале.
Определение. Точки графика непрерывной функции, отделяющие его части выпуклости и вогнутости, называются точками перегиба.
Теорема 6. Если функция y=f(x) дважды дифференцируема на (a;b) и f ¢¢(х)<0 (f ¢¢(х)>0), " x Î(a;b), то график функции y=f(x) на (a;b) является выпуклым (вогнутым).
Теорема 7. (достаточное условие существования точки перегиба). Если f ¢¢(х) при переходе через точку x 0 (в которой f ¢¢(x 0)=0 или ∄ f ¢¢(x 0)) меняет знак, то x 0 – точка перегиба.
Правило исследования функции на выпуклость (вогнутость) и определения точек перегиба
1. Найти Df.
2. Вычислить f ¢¢(х) и найти критические точки 2 рода (f ¢¢(х)=0 или ∄ f ¢¢(х)).
3. Определить знак f ¢¢(х) в промежутках, на которые критические точки делят Df.
4. Найти найти интервалы выпуклости и вогнутости, точки перегиба.
4. 
 Асимптота графика функции y=f(x) – это прямая, расстояние до которой от точки М, лежащей на графике, стремится к нулю при удалении точки М от начала координат по кривой.
Асимптота графика функции y=f(x) – это прямая, расстояние до которой от точки М, лежащей на графике, стремится к нулю при удалении точки М от начала координат по кривой.
вертикальная асимптота
x=a, если  f(x) =±∞ f(x) =±∞
|
наклонная асимптота y=kx+b, если k = b = |
горизонтальная асимптота y=b – частный случай наклонной асимптоты при k =0
|
Схема исследования функции 
- Найти область определения
 функции. Исследовать поведение функции
функции. Исследовать поведение функции  в точках разрыва и на бесконечности.
в точках разрыва и на бесконечности. - В случае, если
 симметрична относительно начала координат, проверить функцию на четность/нечетность; проверить также, не является ли она периодической.
симметрична относительно начала координат, проверить функцию на четность/нечетность; проверить также, не является ли она периодической. - Найти корни функции и промежутки знакопостоянства функции. Точки, в которых
 , т.е. корни функции, – это точки пересечения графика функции с осью Ох. Эти точки являются точками возможной перемены знака у.
, т.е. корни функции, – это точки пересечения графика функции с осью Ох. Эти точки являются точками возможной перемены знака у. - Найти асимптоты графика функции.
- Найти промежутки монотонности функции и точки экстремума, используя производную.
- Найти промежутки выпуклости и вогнутости графика функции, точки перегиба, используя вторую производную
 .
. - Построить график функции, используя результаты исследования. Для уточнения графика можно вычислить значения функции еще в нескольких точках, например можно найти точку пересечения с осью Оу – это точка
 .
.
Пример 1: Исследовать функцию 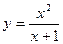 и построить ее график.
и построить ее график.
- Найдем область определения данной функции
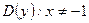 , т.е.
, т.е.  .
.
Исследуем поведение функции на бесконечности:

аналогично  .
.
Поведение функции вблизи точки разрыва  :
:
 ;
;  , т.е.
, т.е.  точка разрыва второго рода.
точка разрыва второго рода.
- Для данной функции область определения
 не симметрична относительно начала координат, следовательно
не симметрична относительно начала координат, следовательно 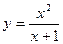 – функция общего вида. Функция алгебраическая, следовательно, не является также и периодической.
– функция общего вида. Функция алгебраическая, следовательно, не является также и периодической. - Из уравнения
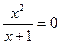 найдем корень функции
найдем корень функции 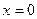 . Найдем промежутки знакопостоянства функции, используя метод промежутков.
. Найдем промежутки знакопостоянства функции, используя метод промежутков.
|
- Так как в точке
 функция терпит разрыв второго рода, то график функции имеет вертикальную асимптоту
функция терпит разрыв второго рода, то график функции имеет вертикальную асимптоту  . Горизонтальных асимптот нет, т.к.
. Горизонтальных асимптот нет, т.к. 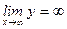 (см. пункт 1). Для отыскания наклонных асимптот
(см. пункт 1). Для отыскания наклонных асимптот  найдем следующие пределы:
найдем следующие пределы:
 ,
,  .
.
Следовательно  наклонная асимптота при
наклонная асимптота при 
- Дифференцируя данную функцию, получим
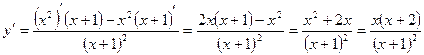 .
.
Производная  при
при 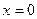 и
и  ,
,  не существует при
не существует при  . Изменение знака производной
. Изменение знака производной  на области определения
на области определения  и монотонность функции
и монотонность функции 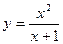 , а также точки экстремума представлены на следующей схеме:
, а также точки экстремума представлены на следующей схеме:
|


|
- Дифференцируя дважды данную функцию, получим
 .
.
Вторая производная  не обращается в нуль, но не существует при
не обращается в нуль, но не существует при  . Однако, точка
. Однако, точка  . Знаки второй производной
. Знаки второй производной  на
на  , а также промежутки выпуклости и вогнутости функции у представлены на схеме:
, а также промежутки выпуклости и вогнутости функции у представлены на схеме:
|
|
Так как в точке  функция не определена, то точек перегиба нет.
функция не определена, то точек перегиба нет.
- Используя полученные данные, строим график функции, см. рис.1
 |
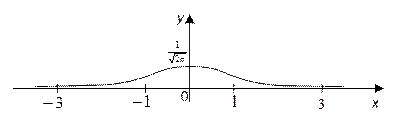
Пример 2: Исследовать функцию Гаусса  и построить ее график.
и построить ее график.

- Область определения
 симметрична относительно точки
симметрична относительно точки 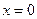 и
и  . Следовательно функция Гаусса является четной функцией и ее график симметричен относительно оси Оу. Дальнейшие исследования можно проводить не на всей
. Следовательно функция Гаусса является четной функцией и ее график симметричен относительно оси Оу. Дальнейшие исследования можно проводить не на всей  , а только при
, а только при  ; построить график на правой полуплоскости и, используя четность, достроить его на левой полуплоскости.
; построить график на правой полуплоскости и, используя четность, достроить его на левой полуплоскости. - Функция Гаусса положительна на
 :
:  . Следовательно график функции располагается в верхней полуплоскости и не пересекает ось Ох.
. Следовательно график функции располагается в верхней полуплоскости и не пересекает ось Ох.
- График функции Гаусса имеет горизонтальную асимптоту
 , т.к.
, т.к.  . Исследуем на наличие наклонных асимптот
. Исследуем на наличие наклонных асимптот  , где
, где  :
:
 .
.
Таким образом, наклонных асимптот нет.
- Найдем первую производную и ее корни:

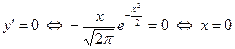
|
|
 на области определения функции и монотонность функции
на области определения функции и монотонность функции  , а также точки экстремума представлены на следующей схеме:
, а также точки экстремума представлены на следующей схеме:
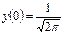
- Исследуем функцию Гаусса на выпуклость/вогнутость, вычислив вторую производную и ее корни:
 ;
;  при
при  .
.
|
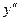 на
на  , а также промежутки выпуклости и вогнутости функции у представлены на схеме:
, а также промежутки выпуклости и вогнутости функции у представлены на схеме:
|
Точки перегиба  , т.к.
, т.к. 
- Функция Гаусса пересекает ось Оу в точке
 .
.
Для уточнения найдем  , это значение очень мало.
, это значение очень мало.
Так как при  функция убывает, а при
функция убывает, а при  возрастает, то
возрастает, то  практически равно нулю при
практически равно нулю при  .
.
Используя результаты исследования, строим график функции Гаусса, который называется купон Гаусса (рис.2)
| |||
|
Варианты с 1 по 34 типового расчета