Числовые ряды – общий член и частичная сумма ряда. Сходимость числовых рядов.
Определение 1.1: Последовательностью действительных чисел называется функция 
, определённая на множестве всех натуральных чисел. Число 
называется 
-ным членом последовательности и обозначается 
, а формула 
называется формулой общего члена последовательности.
Определение 1.2. Пусть имеется некоторая, составленная по определённому закону, бесконечная последовательность чисел 
, чисто формально соединённых между собой знаками плюс:
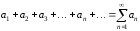. (1)
Такое выражение называется числовым рядом. Числа 
называются членами ряда; 
-ный член ряда 
называется также общим членом ряда. Ряд (1) считается заданным, если известен общий член его, выраженный как функция номера : 
.
Частичная сумма числового ряда – это сумма вида 
, где n – некоторое натуральное число. 
называют также n-ой частичной суммой числового ряда.
Числовой ряд 
называется сходящимся, если существует конечный предел последовательности частичных сумм 
. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд называется расходящимся.
Действия с рядами. Необходимый признак сходимости. Гармонический ряд.
Признаки сравнения числовых рядов. Бесконечно убывающая геометрическая прогрессия.
Бесконечно убывающая геометрическая прогрессия — это прогрессия, у которой |q| < 1. Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии как число, к которому неограниченно приближается сумма 
первых членов рассматриваемой прогрессии при неограниченном возрастании числа .
Формула суммы членов бесконечно убывающей геометрической прогрессии:
|
|
где, q ≠ 1
Знакоположительные ряды. Признак Даламбера.
Если все числа ряда положительны (неположительны, неотрицательны, отрицательны), ряд называется знакоположительным (знаконеположительным, знаконеотрицательным, знакоотрицательным).
Радикальный и интегральный признаки Коши. Ряды Дирихле.
Знакочередующиеся ряды. Признак Лейбница. Свойство частичных сумм сходящегося знакочередующегося ряда.
Частным случаем знакопеременного ряда является знакочередующийся ряд, в котором последовательные члены имеют противоположные знаки.
Пусть знакочередующийся числовой ряд сходится по признаку Лейбница и его сумма равна S. Обозначим через Snчастичную сумму ряда, включающую n членов. Тогда остаток знакочередующегося ряда по абсолютной величине меньше модуля первого отброшенного слагаемого:
|S−Sn|<|an+1|.
Знакопеременные ряды. Достаточный признак сходимости знакопеременных рядов. Абсолютная и условная сходимость.
Числовой ряд, содержащий бесконечное множество положительных членов и бесконечное множество отрицательных членов, называется знакопеременным рядом.
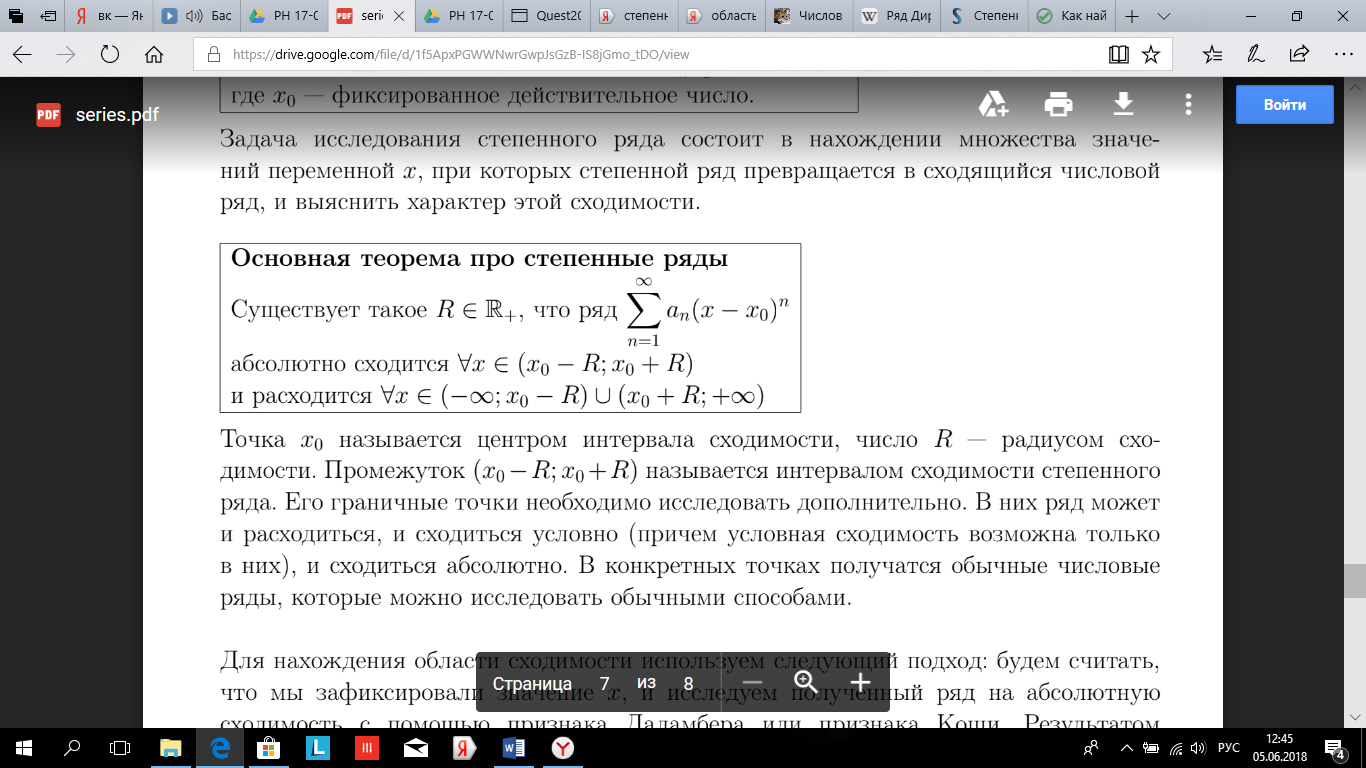
Степенные ряды. Область сходимости. Теорема Абеля для степенных рядов. Формулы для радиуса сходимости степенных рядов.
Под областью сходимости степенных рядов понимается множество значений x при которых ряд сходится.
R=(a-b)/2