Раздел 1.
Точка, прямая, плоскость и их взаиморасположение.
Тема 1. Точка.
Упражнение 1.
Задача 1. По данным координатам точки А (4; 3; 6) постройте косоугольную изометрию (рис.1а) и ортогональные проекции (рис 1б) этой точки (4 – координата точки А по оси OХ; 3 – по оси OY; 6 - по оси OZ).
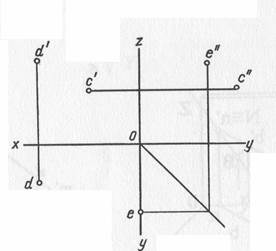
Задача 2. Постройте недостающие проекции точки А, расположенной в I, II, III, IV четвертях пространства.
Тема 2. Точка в различных четвертях (октантах).
Упражнение 2.
Задача 1. Постройте проекции точек, заданных координатами из табл. 1.2. Каждую точку задайте двумя проекциями.
| Точки | x | y | z |
| A | |||
| B | -2 | ||
| C | -3 | -1 | |
| D | -5 | ||
| E | |||
| F | -3 | ||
| G | -2 | -2 | |
| J | -5 | ||
| K | -4 | ||
| L | -3 | ||
| M |
Задача 2. Постройте недостающие проекции точек C, D и E.
Тема 3. Прямая линия.
Упражнение 3.
Следы прямой линии.
Следом прямой называется точка, в которой прямая пересекается с плоскостью проекций (N – фронтальный след, М – горизонтальный).
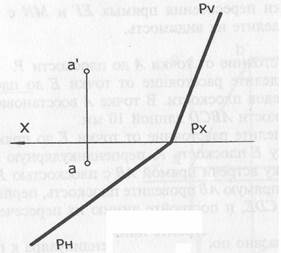
Задача 1 а, б. Постройте косоугольно – изометрический чертеж 1а) и эпюр (1б) отрезка прямой АВ: А (3,1,8); В (10,7,1). По эпюру отрезка определите: а) истинную длину отрезка – на плоскостях Н и V по способу прямоугольной трапеции, а на плоскостях W – по способу прямоугольного треугольника; б) углы наклона α, β, γ к плоскостям Н, V, W; в) следы М и N на плоскостях Н и V.
1а) 1б)
На косоугольно – изометрическом чертеже постройте следы М и N и обозначьте Н.В. отрезка АВ и углы наклона α, β, γ к плоскостям проекций.
Задача 2. Постройте следы прямых АВ и CD и определите Н.В. этих прямых.


Тема 4. Плоскость.
Упражнение 4.
Задача 1. Постройте следы плоскости, заданной треугольником АВС.

Задача 2. Достройте горизонтальную проекцию треугольника АВС, лежащего в плоскости Р.

Задача 3. Определите видимость ребер пирамиды SABC.

Задача 4. Через прямые EF проведите следующие плоскости:
а) плоскость Р – горизонтально проецирующую;
б) плоскость Q – фронтально проецирующую;
в) плоскость R – профильно проецирующую.
Указанные плоскости изобразите двумя пересекающимися прямыми и следами.

Задача 5. Через точку Е проведите отрезок прямой ЕF произвольной длины, параллельный отрезку АВ, и определите расстояние между ними.

Тема 5. Прямая, параллельная плоскость, и две плоскости.
Упражнение 5.
Задача 1. Через точку Е проведите два отрезка прямых, параллельных плоскости Р; отрезок ЕС общего положения произвольной длины и отрезок ЕМ произвольной длины, параллельный профильной плоскости проекций. Определите, параллелен или нет отрезок АВ в плоскости Р.

Задача 2. Через точку А проведите плоскость Q, параллельную плоскости Р.
Задача 3. Постройте проекции точки Т, при надлежащей линии пересечения плоскостей АВСD и I, II, III и отстоящей от плоскости Н на 10 мм.

Задача 4. Постройте проекции линии пересечения плоскостей I, II, III и АВСD. Определите взаимную видимость пересекающихся плоскостей.

Домашнее задание № 1.(Эпюр № 1).
Точка, прямая, плоскость и их взаиморасположение.
Цель задания – закрепить знания по теме «Точка, прямая, плоскость и их взаиморасположение» и приобрести навыки в решение простейших геометрических задач на ортогональном чертеже.
Даны: координаты четырех точек А,В,С,D (точки ВСD определяют треугольник).
Требуется: на ортогональном чертеже выполните следующие задания:
1. постройте следы PН и PV плоскости треугольника BCD и заштрихуйте видимую его часть;
2. определите угол наклона плоскости Р (BCD) к горизонтальной плоскости проекций;
3. через точку А проведите плоскость Q, параллельную заданной плоскости Р;
4. определите расстояние от А до плоскости Р (BCD);
5. постройте следы плоскости (SН и SV), параллельной плоскости Р и отстоящей от нее на три масштабные единицы;
6. через произвольно взятую точку Е проведите плоскость R, перпендикулярную любой стороне треугольника BCD, и определите точку пересечения этой стороны с плоскостью R.
| № задания. | Точки. | Координаты точек. | ||
| X | Y | Z | ||
| 1. | А | 7.5 | ||
| В | ||||
| С | ||||
| D | -7 | |||
| 2. | А | 12.5 | ||
| В | ||||
| С | -5 | |||
| D | ||||
| 3. | А | |||
| В | ||||
| С | ||||
| D | -11 | |||
| 4. | А | 6.5 | ||
| В | 1.5 | |||
| С | -2.5 | 9.5 | ||
| D | -1 | |||
| 5. | А | |||
| В | -2 | |||
| С | 14.5 | 1.5 | ||
| D | -2 | |||
| 6. | А | 16.5 | ||
| В | ||||
| С | -8 | |||
| D | 4.5 | |||
| 7. | А | 16.5 | ||
| В | -2 | |||
| С | 4.5 | |||
| D | ||||
| 8. | А | 19.5 | ||
| В | ||||
| С | -5 | |||
| D | 14.5 | |||
| 9. | А | 8.5 | ||
| В | -2 | |||
| С | -5 | |||
| D | ||||
| 10. | А | |||
| В | -8 | |||
| С | -6 | |||
| D |
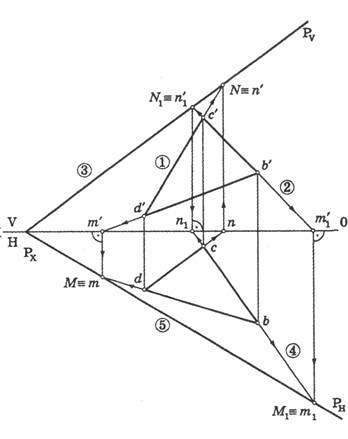
Пример 1. Дана плоскость, заданная треугольником BCD. Постройте следы плоскости PH и PV.
1. Строим фронтальный след плоскости PV. Для этого продолжаем горизонтальную проекцию прямой cd до встречи с осью 0X (точка n), затем из полученной точки n восстанавливаем перпендикуляр к 0X и далее продолжаем проекцию c′ d′ до встречи с перпендикуляром. Получаем фронтальный след прямой – точку N.
2. Аналогично строим следы прямой BC и получаем след N1.
3. Следы N и N1 соединяем и получаем фронтальный след PV.
4 – 5. Аналогично строим следы прямых BC и DC – М и М1.
Соединяем и получаем горизонтальный след плоскости – Pn.
Примечание. При решение этой задачи и в последующих решениях цифры в кружках на рисунках соответствуют позициям 1 – 5 по тексту.
Пример 2. Определите угол наклона плоскости Р к горизонтальной плоскости проекций Н.
1. В плоскости Р на следе PV берем произвольную точку 1′ и находим горизонтальную проекцию – точку 1, лежащую на оси 0Х.
2. Из точки 1 опускаем перпендикуляр на РН (в точку 2) – это горизонтальная проекция (Г.П.) линии наибольшего ската (Л.Н.С.).
3. Найдем Ф.П. линии наибольшего ската – спроецируем точку 2 на ось 0Х и соединим с точкой 1′. Получаем Ф.П.Л.Н.С.
4. Найдем Н.В.Л.Н.С. с помощью способа прямоугольного треугольника.
5. Угол наклона α плоскости Р к плоскости Н определяем между Н.В.Л.Н.С. и ее Г.П.

Пример 3. Через точку А проведите плоскость Q, параллельную заданной плоскости Р.
1. Через горизонтальную проекцию точки А проводим Г.П.Г. будущей плоскости Q, параллельную горизонтальному следу PН.
2. Через а′ проводим Ф.П.Г. параллельно оси 0Х.
3. Из точки n, лежащей на оси, восстанавливаем перпендикуляр до встречи с Ф.П.Г. – получаем точку N.
4. Через точку N проводим QV || PV и доводим след PV до оси 0Х – получаем точку QХ (точка схода следов).
5. Из точки QХ проводим QН || PН.

Пример 4. Определите расстояние от точки А до плоскости Р.
1. Опускаем из точки А перпендикуляр на плоскость.
2. Заключаем перпендикуляр в горизонтально проецирующую плоскость Т.
3. Находим линию пересечения плоскостей Р и Т (прямая МN).
4. Продолжаем фронтальную проекцию перпендикуляра (опущенного из точки а′) до встречи с фронтальной проекцией линии пересечения двух плоскостей (точка к′).
5. Проецируем точку к′ на горизонтальную проекцию прямой МN (получаем точку к).
6. Определяем Н.В. расстояния АК способом прямоугольного треугольника.

Пример 5. Постройте следы (SН, SV) плоскости, параллельной плоскости Р и отстоящей от нее на три масштабные единицы.
1. Из точки схода следов PХ восстанавливаем проекции перпендикуляра к плоскости Р произвольной длины.
2. На этом перпендикуляре берем произвольную точку F.
3. Ищем Н.В. произвольного отрезка PХ F способом прямоугольного треугольника.
4. На Н.В. отрезка F0 PХ откладываем от точки PХ три масштабные единицы – получаем точку 30.
5. Проецируем эту точку на прямую PХ F – получаем точки 3 и 3′.
6. Через точки 3 и 3′ проводим проекции горизонтали (Г.П.Г.) и (Ф.П.Г.) будущей плоскости S и ищем ее фронтальный след N.
7. Через точку N проводим след плоскости S V || PV находим точку схода следов SХ и проводим SН || PН.

Пример6. Через произвольно взятую точку Е проведите плоскость R, перпендикулярную любой стороне треугольника BCD, и определите точку пересечения этой стороны с плоскостью R.
1. Берем произвольную точку Е и через ее проекции проводим Ф.П.Г. || 0Х и Г.П.Г. и bc.
2. Находим фронтальный след построенной горизонтали (точка N).
3. Через точку N проводим след RV и b′ c′ и доводим его до оси 0Х – получаем точку схода следов RХ.
4. Из точки RХ перпендикулярно к стороне bc проводим след RН.
5. Для того чтобы найти точку пересечения прямой ВС с плоскостью R, необходимо заключить прямую ВС в горизонтально проецирующую плоскость Т.
6. Найдем линию пересечения плоскостей R и Т (прямую М1 N1).
7. Отметим на пересечении прямой ВС и М1 N1 точку К.

Тема 6. Способы перемены плоскостей.
Упражнение 6.
Задача 1. Определите расстояние от точки С до прямой АВ.

Задача 2. Определите расстояние между параллельными прямыми АВ и СD.

Задача 3. Определите расстояние между параллельными плоскостями Р и Q.

Задача 4. Определите угол между гранями АВС и АВD методом перемены плоскостей проекций.
