Способы преобразования проекций.
Цель задания – закрепить знания по преобразованию проекционного чертежа и приобрести навыки в решении задач, используя способы вращения (совмещения) и перемены плоскостей проекций.
Дана: треугольная пирамида (четырехгранник) АВСD.
Варианты задач берутся из таблицы.
Требуется на ортогональном чертеже решить следующие задачи.
Задача 1. Определите видимость ребер пирамиды.
Задача 2. Способом вращения вокруг осей, перпендикулярных плоскостям проекций, определите расстояние от точки А до плоскости ВСD.
Задача 3. Вращением вокруг горизонтали постройте натуральную величину треугольника ВСD.
Задача 4. Способом замены плоскостей проекций определить величину двухгранного угла между гранями АВС и АВD.. Найденные величины покажите на первоначальных проекциях.
Задачи решаются комплексно.
Задача 5. Постройте проекции и натуральную величину сечения поверхности проецирующей плоскостью. Варианты заданий берутся в М 2:1.
Задача 6. Постройте сечение поверхности плоскостью общего положения и способом совмещения определите натуральную величину сечения. Варианты заданий берутся в М 2:1.
| № задания. | Точки. | Координаты точек. | ||
| X | Y | Z | ||
| 1. | А | |||
| В | ||||
| С | ||||
| Д | ||||
| 2. | А | |||
| В | ||||
| С | ||||
| Д | ||||
| 3. | А | |||
| В | ||||
| С | ||||
| Д | ||||
| 4. | А | |||
| В | ||||
| С | ||||
| Д | ||||
| 5. | А | |||
| В | ||||
| С | ||||
| Д | ||||
| 6. | А | |||
| В | ||||
| С | ||||
| Д | ||||
| 7. | А | |||
| В | ||||
| С | ||||
| Д | ||||
| 8. | А | |||
| В | ||||
| С | ||||
| Д | ||||
| 9. | А | |||
| В | ||||
| С | ||||
| Д | ||||
| 10. | А | |||
| В | ||||
| С | ||||
| Д |
Решение задач эпюра № 2.
Задача 1. Определите видимость пирамиды. Пирамида строится по координатам точек, взятых в таблице в М 2:1. Видимость прямых определяется с помощью конкурирующих точек.
Например, на прямых АС и ВD на горизонтальной проекции пирамиды берем две точки 1 и 2 и поднимаем их на фронтальные проекции прямых: точку 1 на прямую АС, а точку 2 на ВD. Мысленно смотрим на пирамиду сверху (см.стрелку) – точка 1 выше точки 2, следовательно, прямая ВD будет невидимой. Затем берем на фронтальной проекции точки 3′ и 4′ и проецируем их на горизонтальные проекции прямых АD и ВС. Смотрим по стрелке – точка 3 закрывает точку 4, следовательно, прямая ВС – невидимая.
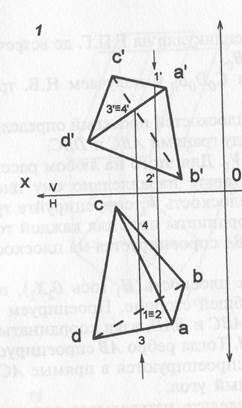
Задача 2. Способом вращения вокруг осей, перпендикулярных плоскостям проекций, определите расстояние от точки А до плоскости ВСD. По координатам точек строим треугольник ВСD и точку А. Задачу можно решить с помощью горизонтали треугольника, поставив горизонталь перпендикулярно к фронтальной плоскости (способ плоскопараллельного перемещения), тогда треугольник на фронтальной плоскости проекций проецируется в прямую. Расстояние от точки А до треугольника ВСD будет определяться длиной перпендикуляра.

Задача 3. Вращением вокруг горизонтали постройте натуральную величину треугольника ВСD.
1. Через точку D проводим горизонталь треугольника (D1).
2. Вращаем точку С вокруг горизонтали. Опустим перпендикуляр из точки с на Г.П.Г. и находим Н.В. радиуса вращения.
3. Из точки b опускаем перпендикуляр на Г.П.Г. дл встречи с прямой С0 1 – получаем точку В0.
4. Соединяем все три точки С0 D0 В0 и получаем Н.В. треугольника.
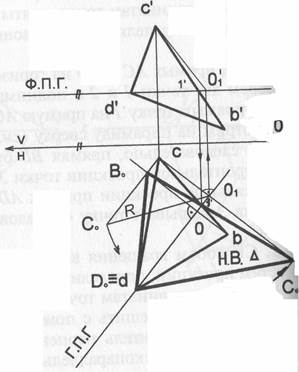
Задача 4. Способом замены плоскостей проекций определите величину двухгранного угла между гранями АВС и АВD.
1. Замените плоскость V на V1. Для этого на любом расстоянии от общего ребра ВА поставьте параллельно ему плоскость V (ось 01 X1) и на новую плоскость V1, спроецируйте треугольники АВС и АВД, взяв координаты по Z для каждой точки с плоскости V. Тогда ребро ВА проецируется на плоскость V1 в Н.В.
2. Плоскость Н заменяем на плоскость Н1 (ось 02 X2), поставив ее перпендикулярно к общей стороне. Проецируем на новую плоскость треугольники АВС и ВАD, взяв координаты Y для каждой точки с плоскости Н. Тогда ребро АВ проецируется в точку, а грани АВС и DВА проецируются в прямые АС и АD, образуя между собой искомый угол.

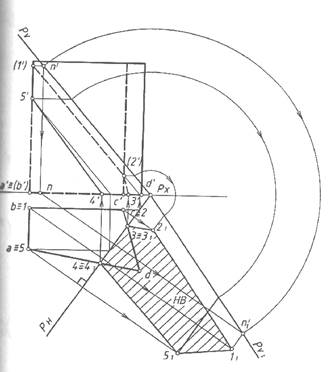
Задача 5. Совмещение определите натуральную величину сечения.
На рисунке показано построение сечения призмы плоскостью. Далее строим Н.В. сечения способом совмещения.
 |