Если механическая система с идеальными связями находится в покое на конечном интервале времени, то равны нулю все силы инерции. Тогда

Это есть принцип виртуальных перемещений.
Используя обобщенные координаты системы и их вариации  , принцип виртуальных перемещений можно записать в следующем виде:
, принцип виртуальных перемещений можно записать в следующем виде:

где  есть обобщенные силы системы.
есть обобщенные силы системы.
В положениях равновесия консервативной системы с идеальными связями равна нулю сумма элементарных работ всех активных сил. Для этих систем обобщенные силы равны
 ,
,
где 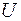 есть потенциальная энергия системы. В этом случае в положениях равновесия потенциальная энергия системы имеет экстремум:
есть потенциальная энергия системы. В этом случае в положениях равновесия потенциальная энергия системы имеет экстремум:

 Задача 5. Определить величину вращающего момента М ворота радиусом R, а также соотношение между массами
Задача 5. Определить величину вращающего момента М ворота радиусом R, а также соотношение между массами  и
и  грузов 1 и 2 для того, чтобы грузы находились в покое. Массами блоков и тросов пренебречь.
грузов 1 и 2 для того, чтобы грузы находились в покое. Массами блоков и тросов пренебречь.
Решение. Система не консервативна и имеет две степени свободы. За обобщенные координаты примем вертикальные координаты 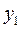 и
и 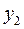 грузов 1 и 2. Уравнение связей в дифференциалах имеют вид:
грузов 1 и 2. Уравнение связей в дифференциалах имеют вид:

Можно проверить, что блоки и тросы есть идеальные связи.
Для решения задачи применим принцип на виртуальных перемещений:

В силу независимости  и
и  , имеем два уравнения:
, имеем два уравнения:

Ответ: 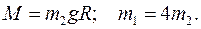
 Задача 6. Однородный тонкий стержень АВ массой
Задача 6. Однородный тонкий стержень АВ массой  и длиной
и длиной  концами А и В скользит по гладким взаимно перпендикулярным направляющим. В точке В к стержню прикреплена нить, перекинутая через блок. К другому концу нити привязан груз М массой
концами А и В скользит по гладким взаимно перпендикулярным направляющим. В точке В к стержню прикреплена нить, перекинутая через блок. К другому концу нити привязан груз М массой  . Определить острый угол
. Определить острый угол  в положении равновесия системы, пренебрегая массами ползунов и блока.
в положении равновесия системы, пренебрегая массами ползунов и блока.
Решение. Система консервативна. Потенциальная энергия системы имеет вид:

Экстремум потенциальной энергии находим из уравнения:

откуда 
Задача 7.Однородные тонкие стержни ОА и АD соединены шарниром А. (AD=4AO). Гладкий  неподвижный упор В и неподвижный шарнир О позволяют системе находиться в покое при угле
неподвижный упор В и неподвижный шарнир О позволяют системе находиться в покое при угле  = 600 стержня ОА с горизонтом. Найти отношение масс стержней. Принять, что ОА=ОВ, а точки О и В находятся на одной горизонтали.
= 600 стержня ОА с горизонтом. Найти отношение масс стержней. Принять, что ОА=ОВ, а точки О и В находятся на одной горизонтали.
Решение. Система находится в равновесии. Все силы инерции равны нулю. Связи идеальны (реакции связей не работают на виртуальных перемещениях системы). Все реакции идеальных связей не являются существенными параметрами, определяющими положение равновесия системы, и поэтому находить их не нужно.
Уравнения связей имеют следующий вид (длина ОА обозначена  ):
):

а в вариациях эти уравнения запишутся так:

В силу этих уравнений, система имеет одну степень свободы. На виртуальных перемещениях работают только силы тяжести стержней ОА и АD, а их элементарная работа определяется вертикальными перемещениями центров масс стержней  и
и  :
:

Принцип виртуальных перемещений окончательно запишется так: 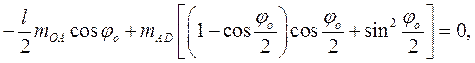 откуда
откуда

Задача 8. Два одинаковых однородных стержня длиной  каждый соединены между собой в точке А шарниром, а концами В и С могут скользить без трения по горизонтальной направляющей. К шарниру А присоединена вертикальная пружина жесткости с, длина которой в недеформированном состоянии равна
каждый соединены между собой в точке А шарниром, а концами В и С могут скользить без трения по горизонтальной направляющей. К шарниру А присоединена вертикальная пружина жесткости с, длина которой в недеформированном состоянии равна  . Найти положения равновесия
. Найти положения равновесия  системы.
системы.

Решение. Потенциальная энергия системы двух тел равна:
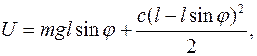
Так как

Имеем четыре положения равновесия:


Задача 9. Система трех точек находится в одном из своих положений равновесия. Найти, каковы должны быть массы  и
и  грузов 1 и 2, удерживаемых грузом 3 с массой
грузов 1 и 2, удерживаемых грузом 3 с массой  на гладких наклонных плоскостях, составляющих углы
на гладких наклонных плоскостях, составляющих углы  и
и  с горизонтом. Пренебречь массами троса и трех блоков, два из которых насажены на одну и ту же ось О.
с горизонтом. Пренебречь массами троса и трех блоков, два из которых насажены на одну и ту же ось О.

Решение. Система из трех грузов имеет идеальные связи (блоки, тросы, гладкие наклонные плоскости), то есть сумма работ их реакций связей равна нулю на виртуальных перемещениях системы. Система имеет две степени свободы. За обобщенные координаты выберем координаты  и
и  , определяющие положения точек на боковых наклонных плоскостях. Уравнение связи, выражающее постоянство длины троса, имеет вид:
, определяющие положения точек на боковых наклонных плоскостях. Уравнение связи, выражающее постоянство длины троса, имеет вид:

Здесь 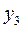 есть вертикальная координата груза 3. В вариациях уравнение связи запишется так:
есть вертикальная координата груза 3. В вариациях уравнение связи запишется так:

Задачу решаем с использованием принципа виртуальных перемещений в форме (15.3).


Получена система двух уравнений с двумя неизвестными  и
и  :
:
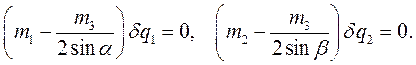
Ответ: 
Другой способ решения задачи 9.
Найдем массы  и
и  грузов 1 и 2, удерживаемые в равновесии грузом 3 массы
грузов 1 и 2, удерживаемые в равновесии грузом 3 массы  на гладких наклонных плоскостях, составляющих углы
на гладких наклонных плоскостях, составляющих углы  и
и  с горизонтом. Пренебречь массами троса и трех блоков, два из которых могут независимо поворачиваться вокруг неподвижной оси О.
с горизонтом. Пренебречь массами троса и трех блоков, два из которых могут независимо поворачиваться вокруг неподвижной оси О.

Решение. Система из трех грузов имеет идеальные связи (блоки, тросы, гладкие наклонные плоскости), то есть сумма работ их реакций связей равна нулю на виртуальных перемещениях системы. Уравнение связей, выражающее постоянство длины троса, имеет вид: 
Здесь 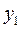 ,
, 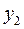 и
и 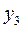 есть вертикальные координаты грузов 1, 2 и 3 соответственно. Примем за независимые координаты (обобщенные координаты)
есть вертикальные координаты грузов 1, 2 и 3 соответственно. Примем за независимые координаты (обобщенные координаты) 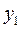 и
и 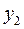 .
.
Работающие на виртуальных перемещениях системы силы тяжести потенциальны. Поэтому можно решить задачу, используя принцип виртуальных перемещений в виде:

Здесь  есть потенциальная энергия системы, равная
есть потенциальная энергия системы, равная
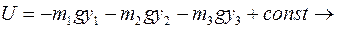
 Экстремум функции
Экстремум функции  в положении равновесия запишется в виде двух уравнений
в положении равновесия запишется в виде двух уравнений
 откуда
откуда 
 Задача 10. Однородные тонкие стержни АО и ОВ одинаковой длины опираются на шероховатую горизонтальную поверхность и, соединенные цилиндрическим шарниром О, находятся в покое в вертикальной плоскости. Чему равен коэффициент трения скольжения f, если система находится в покое при минимальном угле
Задача 10. Однородные тонкие стержни АО и ОВ одинаковой длины опираются на шероховатую горизонтальную поверхность и, соединенные цилиндрическим шарниром О, находятся в покое в вертикальной плоскости. Чему равен коэффициент трения скольжения f, если система находится в покое при минимальном угле  стержней с плоскостью? Найти при этом угле силу
стержней с плоскостью? Найти при этом угле силу  взаимодействия стержней.
взаимодействия стержней.
Решение. Считая, что виртуальные перемещения системы могут происходить только в вертикальной плоскости, покажем, что система двух стержней, соединенных цилиндрическим шарниром О, имеет две степени свободы. Свободное твердое тело в плоском движении имеет три степени свободы. Уравнения связей имеют вид (АО = ОВ =b):

Тогда шесть параметров  двух тел связаны четырьмя уравнениями связей в вариациях:
двух тел связаны четырьмя уравнениями связей в вариациях:

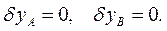
В системе имеется две независимые вариации координат (n = 6 – 4 = 2). Выбор независимых координат не единственен. Пусть независимыми виртуальными перемещениями будут  и
и  . Взаимодействие системы с Землей определяется для каждого стержня силой тяжести
. Взаимодействие системы с Землей определяется для каждого стержня силой тяжести  . Взаимодействие стержней с негладкой плоскостью определяется реакциями
. Взаимодействие стержней с негладкой плоскостью определяется реакциями  и
и  в точках А и В:
в точках А и В:

Взаимодействие стержней между собой в шарнире О определяется силой

Применим дифференциальный принцип на виртуальных (независимых) перемещениях  и
и  , а затем на вертикальном перемещении
, а затем на вертикальном перемещении  всей системы поступательно вверх (перемещении, не совместимом со связями):
всей системы поступательно вверх (перемещении, не совместимом со связями):



Наконец, чтобы найти силу  взаимодействия стержней, дадим стержню АО сначала поступательное горизонтальное, а затем поступательное вертикальное перемещение (оба перемещения не совместимы со связями) и приравняем к нулю каждую из работ. Получим два уравнения для нахождения
взаимодействия стержней, дадим стержню АО сначала поступательное горизонтальное, а затем поступательное вертикальное перемещение (оба перемещения не совместимы со связями) и приравняем к нулю каждую из работ. Получим два уравнения для нахождения  ,
,  :
:

Решая эти уравнения, получим:
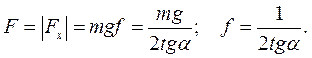
Задача 11. Составная конструкция состоит из двух одинаковых балок АВ и ВС массой m каждая, соединенных цилиндрическим шарниром В. Конец А горизонтальной балки АВ длиной  жестко заделан в стену, а конец С балки ВС стоит на горизонтальных катках. Острый угол между балками равен α. Балка ВС нагружена равномерно распределенной нагрузкой постоянной интенсивности q, перпендикулярной плоскости балки. Найти реакцию заделки балки АВ в стену, если система покоится.
жестко заделан в стену, а конец С балки ВС стоит на горизонтальных катках. Острый угол между балками равен α. Балка ВС нагружена равномерно распределенной нагрузкой постоянной интенсивности q, перпендикулярной плоскости балки. Найти реакцию заделки балки АВ в стену, если система покоится.

Решение. Система не имеет виртуальных перемещений (элементарных перемещений, совместимых со связями), другими словами - не имеет степеней свободы и находится в покое. Поэтому применим дифференциальный принцип на перемещениях, не совместимых со связями, ко всей системе, а затем к ее частям. В задаче имеется пять скалярных неизвестных параметров взаимодействия балок со стеной и между собой. Согласно аксиомам реакций связей

Шесть неизвестных могли бы быть найдены из шести скалярных уравнений равновесия, вытекающих из принципа. Однако дифференциальный принцип позволяет написать меньшее число уравнений для нахождения трех неизвестных задачи: двух компонент 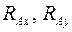 главного вектора распределенных сил реакций заделки (плоская система сил) и одной компоненты
главного вектора распределенных сил реакций заделки (плоская система сил) и одной компоненты  главного момента этих сил.
главного момента этих сил.
Для решения задачи достаточно написать три уравнения с тремя искомыми неизвестными. Так как все перемещения несовместимы со связями, то они произвольны и независимы.
Приравняем к нулю работу всех сил на горизонтальном перемещении системы (цилиндрический шарнир В – идеальная связь):
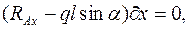
Приравняем к нулю работу всех сил на элементарном повороте  системы вокруг точки С:
системы вокруг точки С:
 Наконец, для балки АВ приравняем к нулю работу всех сил на ее повороте
Наконец, для балки АВ приравняем к нулю работу всех сил на ее повороте  вокруг точки В:
вокруг точки В:

Заметим, что два последних уравнения эквивалентны некоторым из уравнений равновесия системы и балки АВ, а именно: равенство нулю главных моментов всех внешних сил для системы (относительно точки А) и всех сил балки АВ (относительно точки В). Наконец, первое уравнение эквивалентно уравнению равновесия всей системы в проекции на горизонталь.
Далее достаточно решить систему трех алгебраических уравнений с тремя неизвестными.
Задание. Найти силы реакций шарниров В и С. Например, для балки ВС приравняем к нулю элементарную работу всех сил на ее элементарном повороте вокруг точки В:

Ответ:

 Задача 12. Два тяжелых однородных стержня ОА и АВ соединены цилиндрическим шарниром в точке А. Стержень ОА может вращаться вокруг неподвижной оси О, а стержень АВ опирается на неподвижный гладкий гвоздь D, расположенный на одной горизонтали с точкой О, причем ОА = ОD. Стержень АВ вдвое длиннее и тяжелее стержня ОА. Приняв угол
Задача 12. Два тяжелых однородных стержня ОА и АВ соединены цилиндрическим шарниром в точке А. Стержень ОА может вращаться вокруг неподвижной оси О, а стержень АВ опирается на неподвижный гладкий гвоздь D, расположенный на одной горизонтали с точкой О, причем ОА = ОD. Стержень АВ вдвое длиннее и тяжелее стержня ОА. Приняв угол 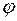 за обобщенную координату, найти положение равновесия системы в интервале
за обобщенную координату, найти положение равновесия системы в интервале  .
.
Решение. Консервативная система с одной степенью свободы имеет потенциальную энергию

где l есть длина, m есть масса стержня ОА. Положение равновесия  находится из условия экстремальности в нем потенциальной энергии из уравнения:
находится из условия экстремальности в нем потенциальной энергии из уравнения:  .
.
Ответ:  .
.
 Задача 13. Мотор А, создающий постоянный вращающий момент М, должен равномерно и вертикально перемещать грузы 1 и 2. Какие ограничения на массы m1 и m2 грузов 1 и 2 накладывает данная система блоков, если масса каждого блока равна m, а радиус ворота мотора равен R. Массой тросов пренебречь.
Задача 13. Мотор А, создающий постоянный вращающий момент М, должен равномерно и вертикально перемещать грузы 1 и 2. Какие ограничения на массы m1 и m2 грузов 1 и 2 накладывает данная система блоков, если масса каждого блока равна m, а радиус ворота мотора равен R. Массой тросов пренебречь.
Решение. В систему включаем грузы 1 и 2 и оба подвижных блока. Условие постоянства длины нити, перекинутой через верхний блок с неподвижной осью, и условие отсутствия проскальзывания тросов по блокам запишем в виде уравнений связей в дифференциалах:

Здесь 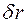 есть виртуальное перемещение вверх середины левого блока,
есть виртуальное перемещение вверх середины левого блока,  есть виртуальное перемещение вниз первого груза,
есть виртуальное перемещение вниз первого груза,  есть перемещение вверх второго груза, а
есть перемещение вверх второго груза, а  есть элементарный возможный поворот мотора против часовой стрелки.
есть элементарный возможный поворот мотора против часовой стрелки.
Далее примем, что  и
и  виртуально независимы, тогда остальные виртуальные перемещения выражаются через них из уравнений связей. Поэтому система имеет 2 степени свободы.
виртуально независимы, тогда остальные виртуальные перемещения выражаются через них из уравнений связей. Поэтому система имеет 2 степени свободы.
Принцип виртуальных перемещений для системы запишется в виде:
 В силу независимости и произвольности
В силу независимости и произвольности  и
и  , имеем два уравнения:
, имеем два уравнения:

Система блоков и тросов, не смотря на различные натяжения тросов по обе стороны каждого весомого блока, является идеальной связью. Натяжения тросов (внутренние силы системы) не влияют на соотношение масс грузов в равновесии. Значит, писать уравнения, в которые входят натяжения тросов, нет необходимости. Дифференциальный принцип это подтверждает.
Ответ: 
Задача 14. Определить реакцию заделки в стену горизонтальной однородной балки ОО1 длиной 2L и массой m, если ее отягощают два однородных круглых цилиндра с массами m1 и m2 , соединенных симметрично двумя невесомыми нитями, намотанными на оба цилиндра. Центр масс О2 цилиндра 2 движется вертикально, а цилиндр 1 вращается вокруг шарнира О1.
 Решение. Так как в задаче нужно найти внешнюю реакцию связей системы, то необходимо составлять такие уравнения движения, в которых внутренние силы всей системы (подсистемы) отсутствуют. В то же время искомая реакция зависит от движения системы, поэтому кинематические характеристики этого движения будут необходимы для решения задачи. По аксиоме связей плоская реакция заделки в стену характеризуется главным вектором
Решение. Так как в задаче нужно найти внешнюю реакцию связей системы, то необходимо составлять такие уравнения движения, в которых внутренние силы всей системы (подсистемы) отсутствуют. В то же время искомая реакция зависит от движения системы, поэтому кинематические характеристики этого движения будут необходимы для решения задачи. По аксиоме связей плоская реакция заделки в стену характеризуется главным вектором 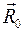 и главным моментом
и главным моментом  сил относительно точки О:
сил относительно точки О:

Поэтому решение должно содержать не менее трех уравнений. За обобщенные координаты системы возьмем координату y 2 центра масс цилиндра 2 и углы поворота  и
и  цилиндров.
цилиндров.
Уравнения связей в дифференциалах и в производных от уравнений связей имеют вид:

Здесь  и
и  есть радиусы оснований цилиндров 1 и 2 соответственно.
есть радиусы оснований цилиндров 1 и 2 соответственно.
Система имеет 2 степени свободы. В силу уравнения связей за независимые виртуальные перемещения примем углы поворотов цилиндров  и
и  .
.
Так как связи идеальны, то дифференциальный вариационный принцип сначала применим в форме принципа Даламбера – Лагранжа:

где  ,
,  , и
, и  по определению есть
по определению есть

С использованием уравнений связей для ускорений, получим замкнутую систему трех уравнений

из которых найдем ускорение  центра масс второго цилиндра:
центра масс второго цилиндра:

Далее, для получения трех компонент реакции заделки в стену применим ко всей системе вариационный дифференциальный принцип на перемещениях, не совместимых со связями. На любом из них сумма работ всех сил (здесь внешних), а также всех главных векторов и главных моментов сил инерций, равна нулю. Поэтому, на поступательном перемещении  вниз по вертикали, затем на поступательном перемещении
вниз по вертикали, затем на поступательном перемещении  вправо по горизонтали, и, наконец, на повороте
вправо по горизонтали, и, наконец, на повороте 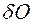 вокруг оси
вокруг оси  приравняем к нулю сумму работ всех внешних активных сил, всех сил и моментов сил инерций. В результате получим уравнения:
приравняем к нулю сумму работ всех внешних активных сил, всех сил и моментов сил инерций. В результате получим уравнения:

Отметим, что внутренние взаимодействия тел системы (взаимодействие балки ОО1 с блоком 1 натяжение нити) Не вошли в уравнения – это несущественные параметры для нахождения внешней силы реакции связи в точке О.
Ответ: 

 Задача 15. Два одинаковых однородных гладких стержня АВ и СD, массой m каждый, соединены цилиндрическим шарниром Е, поставлены на гладкий горизонтальный пол, и, соединенные нитью КL, находятся в равновесии. Квадратная пластина массой m1, имеющая длину боковой стороны s, расположена между стержнями сверху, как показано на рисунке. Найти натяжение нити как функцию угла
Задача 15. Два одинаковых однородных гладких стержня АВ и СD, массой m каждый, соединены цилиндрическим шарниром Е, поставлены на гладкий горизонтальный пол, и, соединенные нитью КL, находятся в равновесии. Квадратная пластина массой m1, имеющая длину боковой стороны s, расположена между стержнями сверху, как показано на рисунке. Найти натяжение нити как функцию угла  наклона стержней к вертикали. Принять, что АЕ = ЕВ = ЕD = СЕ = b, ЕL = EK= =АК = LС.
наклона стержней к вертикали. Принять, что АЕ = ЕВ = ЕD = СЕ = b, ЕL = EK= =АК = LС.
Решение. Система не имеет степеней свободы, поэтому дифференциальный принцип применим с использованием элементарных перемещений, не совместимых со связями.
Так как силы взаимодействия стержней в шарнире Е, в точках касания стержней с горизонтальной плоскостью, а также в местах касания пластины со стержнями не работают на любых перемещениях системы (связи идеальны), то работать на них будут только силы тяжести и реакция нити.
Дифференциальный вариационный принцип будет иметь вид:
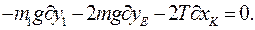
Здесь  есть элементарные перемещения, на которых работают соответственно силы тяжести
есть элементарные перемещения, на которых работают соответственно силы тяжести  и реакции нити Т. Перемещения получены варьированием по углу
и реакции нити Т. Перемещения получены варьированием по углу  (дифференцированием) необходимых координат точек приложения соответствующих сил:
(дифференцированием) необходимых координат точек приложения соответствующих сил:

Дифференциальный вариационный принцип имеет вид:

Ввиду произвольности элементарного перемещения  , получаем уравнение
, получаем уравнение

из которого для каждого острого угла  находится реакция нити:
находится реакция нити:

Задача 16. Составная конструкция состоит из двух однородных сплошных балок АВ и СD c массами m1 и m2 соответственно, соединенных в точке С цилиндрическим шарниром. В точках А и D имеется цилиндрический шарнир на подвижной опоре, а в точке В цилиндрический шарнир на неподвижной опоре. Половина балки  отягощена равномерно распределенной нагрузкой интенсивности q (масса на единицу длины), а к балке СD приложен вращающий момент М. Угол балки СD с горизонтом равен
отягощена равномерно распределенной нагрузкой интенсивности q (масса на единицу длины), а к балке СD приложен вращающий момент М. Угол балки СD с горизонтом равен  . Определить реакции связей системы в точках А, В и D.
. Определить реакции связей системы в точках А, В и D. 
Решение. Система не имеет степеней свободы. Поэтому дифференциальный вариационный принцип применим к системе и к ее части СD на перемещениях, не совместимых со связями.
Выберем декартовы оси координат Оxy, как показано на рисунке. Согласно аксиомам реакций связей задача имеет четыре неизвестных алгебраических компоненты сил реакций связей:

Для решения задачи составим четыре независимых уравнения с четырьмя необходимыми неизвестными  . Для этого элементарные перемещения выбраны так, чтобы неизвестная сила реакции в шарнире С не вошла в уравнения, то есть не работала на выбранной системе элементарных поступательных перемещений
. Для этого элементарные перемещения выбраны так, чтобы неизвестная сила реакции в шарнире С не вошла в уравнения, то есть не работала на выбранной системе элементарных поступательных перемещений  ,
, 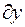 , элементарном повороте
, элементарном повороте  вокруг точки В для всей системы и элементарном повороте
вокруг точки В для всей системы и элементарном повороте  вокруг точки С балки СD.
вокруг точки С балки СD.
Четыре уравнения принципа запишутся в следующем виде:



Так как элементарные перемещения произвольны, то, сокращая уравнения на элементарные перемещения, получим четыре искомых уравнения с четырьмя неизвестными. Эти уравнения эквивалентны уравнениям равновесия системы.
Ответ:



 Задача 17, Мещерский, (41.23). Однородный тонкий прямолинейный однородный стержень АВ шарнирно соединен с вертикальным валом в точке О. Вал вращается с постоянной угловой скоростью
Задача 17, Мещерский, (41.23). Однородный тонкий прямолинейный однородный стержень АВ шарнирно соединен с вертикальным валом в точке О. Вал вращается с постоянной угловой скоростью  .Определить угол отклонения
.Определить угол отклонения  стержня от вертикали, если ОА = а, ОВ = b.
стержня от вертикали, если ОА = а, ОВ = b.
Решение. Выберем в стержне систему координат Оxyz, где ось Оx направлена вдоль АВ, а ось Оz – вдоль оси шарнира О. Вектор угловой скорости  и вектор углового ускорения
и вектор углового ускорения  имеют в этих осях следующий вид:
имеют в этих осях следующий вид:

Пусть  есть линейная массовая плотность стержня АВ:
есть линейная массовая плотность стержня АВ: 
Главный момент сил инерции  относительно неподвижной точки О равен:
относительно неподвижной точки О равен:

Так как



а главный момент силы тяжести, как сумма моментов его частей АО и ОВ, относительно точки О есть
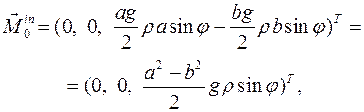
то элементарную работу момента силы тяжести и момента сил инерции стержня вычисляем на перемещении  , не совместимом со связями, по формуле
, не совместимом со связями, по формуле

Дифференциальный вариационный принцип, после сокращения на  , дает уравнение:
, дает уравнение:

Заметим, что такой же результат дает теорема об изменении момента импульса стержня относительно неподвижной точки О, записанная в подвижных осях:

Ответ: 
Задача 18. Мещерский, (42.4). К вертикальной оси АВ, вращающейся равноускоренно с угловым ускорением, жестко прикреплены два точечных груза Е и D посредством двух невесомых стержней ОЕ = ОD = r, перпендикулярных как между собой, так и к оси АВ. Определить динамические давления оси АВ на подпятник А и подшипник В для любого момента времени, если в начальный момент система покоилась. Масса каждого груза равна mо. Найти также вращающий момент  , необходимый для заданного движения системы.
, необходимый для заданного движения системы.
 Решение. Объектом движения является абсолютно твердое тело, состоящее из оси АВ и стержней ОС и ОD. Ось и стержни считаем невесомыми.Массы имеют только точки Е и D. Свяжем с телом подвижные оси координат Оxy. Взаимодействие тела со связями (подшипник и подпятник) определяется третьим законом Ньютона и аксиомами сил акций (давлений на подшипник и подпятник) и реакций
Решение. Объектом движения является абсолютно твердое тело, состоящее из оси АВ и стержней ОС и ОD. Ось и стержни считаем невесомыми.Массы имеют только точки Е и D. Свяжем с телом подвижные оси координат Оxy. Взаимодействие тела со связями (подшипник и подпятник) определяется третьим законом Ньютона и аксиомами сил акций (давлений на подшипник и подпятник) и реакций  и
и  в точках А и В:
в точках А и В:

Динамическими давлениями называются те слагаемые полных давлений, которые определяются движением, его кинематическими характеристиками, в отличие от статических давлений, определяемых только активными силами. В уравнения движения входят полные реакции  и
и  . Их компоненты мы сначала и найдем.
. Их компоненты мы сначала и найдем.
В системе нет виртуальных перемещений. Поэтому для решения задачи применим дифференциальный вариационный принцип на элементарных перемещениях твердого тела, не совместимых со связями (они произвольны и независимы). Пусть это будут либо поступательные перемещения тела вдоль осей координат  либо его повороты
либо его повороты  вокруг осей координат.
вокруг осей координат.
Запишем дифференциальный вариационный принцип механики на перемещениях, не совместимых со связями:

где  есть элементарная работа силы тяжести и вращающего момента
есть элементарная работа силы тяжести и вращающего момента  ,
,  - элементарная работа сил реакций, а
- элементарная работа сил реакций, а  - элементарная работа сил инерций
- элементарная работа сил инерций
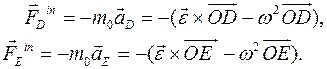
В силу независимости и произвольности перемещений  , можно приравнять к нулю элементарную работу всех сил на каждом элементарном перемещении:
, можно приравнять к нулю элементарную работу всех сил на каждом элементарном перемещении:

Заметим, что полученные уравнения эквивалентны дифференциальным уравнениям движения твердого тела, а также уравнениям кинетостатики.
Из шести уравнений с шестью неизвестными находим компоненты реакций связей:



Наконец, для нахождения компонент сил давления  удалим из компонент сил реакций слагаемые с силой тяжести
удалим из компонент сил реакций слагаемые с силой тяжести 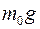 и поменяем знаки у проекций векторов (третий закон Ньютона):
и поменяем знаки у проекций векторов (третий закон Ньютона):

Ответ:

 Задача 19. На гладкой горизонтальной плоскости помещена треугольная призма с гладким основанием. По шероховатой наклонной грани призмы скатывается без скольжения однородный сплошной круглый цилиндр массы m1. Определить силу взаимодействия призмы и цилиндра. Масса призмы равна m, угол наклонной грани призмы с горизонтом равен
Задача 19. На гладкой горизонтальной плоскости помещена треугольная призма с гладким основанием. По шероховатой наклонной грани призмы скатывается без скольжения однородный сплошной круглый цилиндр массы m1. Определить силу взаимодействия призмы и цилиндра. Масса призмы равна m, угол наклонной грани призмы с горизонтом равен  .
.
Решение. Виртуальные перемещения системы из любого ее положения совместимы со связями, если призма и цилиндр, а также призма и горизонтальная плоскость находятся в контакте на возможных перемещениях, совместимых со связями. Очевидно, что связи не нарушатся, если цилиндр перекатывать без проскальзывания по фиксированной призме, поворачивая ее на элементарный угол. Наоборот, если фиксировать, то поступательное перемещение всей системы тоже не нарушает связей. Тогда и виртуально независимы. Система имеет две степени свободы. Рассмотрим теперь действительное движение системы. Цилиндр, скатываясь по боковой грани призмы вниз, давит на призму и движет ее влево. Пусть ускорение призмы есть  . Рассмотрим движение цилиндра как сложное: по отношению к призме (относительное движение цилиндра) и вместе с призмой (переносное движение цилиндра). Относительное ускорение центра масс цилиндра вдоль боковой грани призмы обозначим
. Рассмотрим движение цилиндра как сложное: по отношению к призме (относительное движение цилиндра) и вместе с призмой (переносное движение цилиндра). Относительное ускорение центра масс цилиндра вдоль боковой грани призмы обозначим  , а его абсолютное угловое ускорение -
, а его абсолютное угловое ускорение -  . По теореме сложения ускорений для точки С (центра масс цилиндра), в сложном движении абсолютное ускорение точки С равно:
. По теореме сложения ускорений для точки С (центра масс цилиндра), в сложном движении абсолютное ускорение точки С равно:


где  есть радиус основания цилиндра.
есть радиус основания цилиндра.
Тогда главный вектор сил инерций призмы и главный вектор сил инерций цилиндра равен

а главный момент сил инерций цилиндра относительно точки С

Здесь  - момент инерции цилиндра относительно оси цилиндра.
- момент инерции цилиндра относительно оси цилиндра.
Перейдем к рассмотрению взаимодействий тел системы. Используем аксиомы активных сил и сил реакций. Действие Земли (акция) определяется силами тяжести (активными силами) призмы и цилиндра.
Противодействие гладкой неподвижной горизонтальной плоскости на призму определяется силой противодействия (силой реакции) плоскости, перпендикулярной неподвижной плоскости.
Взаимодействие призмы и цилиндра (внутреннее взаимодействие системы) для цилиндра определяется силой реакции  , имеющей составляющую
, имеющей составляющую  вдоль наклонной поверхности в сторону, противоположную движению, и нормальной составляющей
вдоль наклонной поверхности в сторону, противоположную движению, и нормальной составляющей  , перпендикулярной наклонной плоскости (от нее):
, перпендикулярной наклонной плоскости (от нее):

Связи системы (гладкая горизонтальная плоскость и качение цилиндра без проскальзывания) идеальны, то есть контактные силы в