Дифференциальный принцип механики системы тел с геометрическими связями.

Дифференциальный принцип механики.

Методическое пособие.

Введение. Дифференциальный принцип механики есть метод решения задач динамики и статики для систем твердых тел, положения и движения которых подчинены геометрическим стационарным связям.

В задачах динамики различные формы уравнений движения тел системы, записанные единым методом, позволяют находить движение тел и их взаимодействие. В задачах статики метод определяет условия, при которых система тел находится в покое, и находит силовые взаимодействия тел.

В пособии проведено сравнение двух методов получения уравнений движения - дифференциального принципа механики и теорем динамики в дифференциальной форме. В системах, в которых действуют идеальные, потенциальные, центральные, силы с осевой симметрией, для нахождения движения используются первые интегралы уравнений движения (законы сохранения).

Понятия и определения.

Пусть N тел, выбранных из материальной системы, взаимодействуют между собой и с другими телами системы, а на положения тел наложены ограничения (связи).

1. Положения тел по отношению к инерциальной системе отсчета определяют 6N скалярных параметров (координаты, углы), то есть . Положение удовлетворяет геометрическим уравнениям связей

Говорят, что совместимо со связями. При этом движение удовлетворяет еще и уравнениям связей в кинематической форме, полученным дифференцированием по времени один или два раза геометрических уравнений связей.

Скалярные функции векторного аргумента дважды непрерывно дифференцируемы по времени. Функционально независимые уравнения связей, для любого положения системы, совместимого со связями, позволяют из уравнений связей в вариациях

выбрать независимых элементарных перемещений , которые удовлетворяют уравнениям связей в вариациях в следующем виде:

Элементарные перемещения называются виртуальными (возможными) перемещениями. Скалярные параметры (координаты и углы) которые соответствуют независимым виртуальным перемещениям , называются обобщенными координатами. Говорят, что в иртуальные перемещения совместимы со связями.

Число 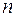обобщенных координат, определяющих положение N твердых тел, называется числом степеней свободы этих тел.

Пример. Плоское качение цилиндра без проскальзывания по негладкой плоскости.

В общем случае положение твердого тела определяется шестью координатами – тремя координатами полюса в теле, и тремя углами поворота. В данном примере шесть параметров связаны пятью уравнениями связей:

Условие качения без проскальзывания выражает первое уравнение. В нем для некоторой точки К на поверхности цилиндра принято, что в начальном положении (К₀) она находилась в начале координат. Цилиндр имеет одну степень свободы, так как ненулевые виртуальные перемещения (вариации координат) связаны одним уравнением связей в дифференциалах (вариациях):

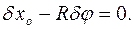
Не совместимые со связями элементарные перемещения системы тел произвольны, независимы и не удовлетворяют уравнениям связей.

2. Силы инерции твердого тела. Главный вектор и главный момент сил инерций тела.

Поле элементарных сил инерций твердого тела определяется по Даламберу

по полю абсолютных ускорений всех элементарных масс тела, положение которых по отношению к центру масс С задается векторами 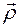. При этом поле ускорений имеет вид:

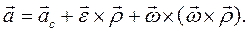
Здесь есть абсолютное ускорение центра масс тела, - абсолютная угловая скорость, а - абсолютное угловое ускорение тела. В системе координат, связанной с телом, векторы 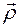постоянны.

Определение. Для тела вектор

есть главный вектор сил инерции, а вектор

есть главный момент сил инерции относительно центра масс С.

В системе координат, связанной с телом, главный момент сил инерций вычисляется по формуле

Здесь 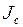есть оператор инерции тела относительно центра масс С. В системе координат, связанной с телом, элементы его матрицы постоянны.

Для плоского и вращательного движений твердого тела угловая скорость тела 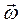и кинетический момент 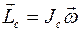параллельны и постоянны по направлению, поэтому

.

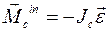3. Работа системы сил на элементарном перемещении твердого тела.

Положение твердого тела определяется вектором положения полюса и собственной ортогональной матрицей ориентации подвижного базиса по отношению к неподвижному базису O. Положение любой точки тела , (), задается в неподвижной системе координат вектором 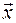следующим образом:

Элементарное изменение (вариация) положения тела определяется изменением положения всех его точек векторами:

где 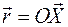, а вектор элементарного поворота определяется кососимметричностью матрицы .

Далее в качестве полюса выберем центр масс тела С. Элементарная работа всех сил твердого тела, линии действия которых проходят через точки тела 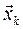, а элементарные перемещения - векторами , равна:

Здесь есть главный вектор всех действующих на тело сил, а есть главный момент этих сил относительно центра масс.

Если на векторы и твердого тела наложены связи, то число независимых вариаций координат меньше шести. В этом случае элементарную работу активных сил можно вычислять на независимых элементарных перемещениях :

где есть обобщенные силы системы.

Элементарная работа сил инерций твердого тела вычисляется следующим образом:

Здесь есть главный вектор сил инерций, а - главный момент сил инерций твердого тела, а элементарное перемещение центра масс и вектор элементарного поворота тела определяются полем элементарных перемещений точек тела.

Виртуальная работа сил инерций при наличии связей вычисляется так же, но виртуальные перемещения удовлетворяют еще и уравнениям связей в вариациях.

Дифференциальный принцип механики системы тел с геометрическими связями.

В любом положении системы N твёрдых тел, допускаемом связями, сумма элементарных работ всех сил взаимодействий и всех сил инерций равна нулю на любых элементарных перемещениях системы из данного положения:

Здесь 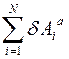есть элементарная работа активных сил системы, есть элементарная работа сил контактного взаимодействия, а - элементарная работа сил инерции в любом положении системы, совместимом со связями.

Подчеркнем. что элементарные перемещения системы со связями могут быть как совместимы, так и не совместимы со связям, однако положения тел всегда совместимы со связями.