ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений OABCD задачи линейного программирования имеет вид:
Тогда максимальное значение функции 
достигается
в точке …
| D | ||
| B | |||
| A | |||
| C |
Решение:
Построим линию уровня 
и градиент целевой функции 
Тогда целевая функция будет принимать максимальное значение в точке «выхода» линии уровня из области допустимых решений в направлении градиента.
Из рисунка видно, что точкой максимума будет точка D как точка «выхода» линии уровня 
из области допустимых решений в направлении градиента.
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Теория игр: игры с природой
Дерево решений в игре с природой имеет вид:
Тогда оптимальной по критерию Байеса является стратегия …
|
| 
| ||
| |||
| |||
| нет оптимальных стратегий |
Решение:
Рассчитаем ожидаемые денежные оценки:
Тогда оптимальной является стратегия, которой соответствует максимальная ожидаемая денежная оценка: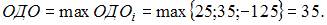 
Это соответствует стратегии 
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Сетевое планирование и управление
Для сетевого графика, изображенного на рисунке,
критическими являются работы …
|
|  и 
| ||
 и 
| |||
 и 
| |||
и 
|
Решение:
Выделим полные пути:
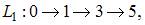
вычислим их длины: 
Критическим путем называется наиболее продолжительный (по времени) полный путь, поэтому это путь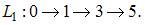 
Тогда критическими будут работы 
и 
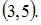
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Транспортная задача
Транспортная задача, заданная распределительной таблицей, имеет вид
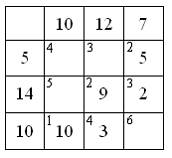
Тогда первоначальное распределение поставок, осуществленное по методу «северо-западного угла» будет иметь вид …
|
| 
| ||
| |||
| |||
|
Решение:
Метод «северо-западного угла» означает, что максимально возможная поставка всегда осуществляется в «северо-западную» клетку распределительной таблицы.
Первоначально поставку осуществляем в клетку с номером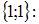 
выбираем наименьшее значение между мощностью поставщика и потребностью потребителя, то есть 
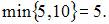От первого поставщика больше перевезти нельзя, поэтому остальные клетки в строке будут пустые, а у потребителя осталась потребность в 10 – 5=5 единицах товара. Следующая клетка с номером 
Первому потребителю больше товара не требуется, поэтому клетка 
пустая, у второго поставщика осталось
14 – 5=9. Следующая клетка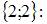 
клетка 
пустая,
12 – 9=3. Следующая клетка 
10 – 3=7. Следующая клетка 
Следовательно, первоначальное распределение будет иметь вид:
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений ABCD задачи линейного программирования имеет вид:
Тогда функция 
достигает максимального значения …
|
| на отрезке AB | ||
| на отрезке CD | |||
| в точке D | |||
| только в точке B |
Решение:
Построим линию уровня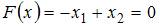 
и градиент целевой функции 
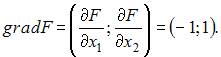Тогда целевая функция будет принимать максимальное значение в точках «выхода» линии уровня из области допустимых решений в направлении градиента.
Из рисунка видно, что точки максимума будут лежать на отрезке CD как на точках «выхода» линии уровня из области допустимых решений в направлении градиента.
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Транспортная задача
Транспортная задача, заданная распределительной таблицей, имеет вид
Тогда первоначальное распределение поставок, осуществленное по методу «учета наименьших затрат» будет иметь вид …
|
| 
| ||
| |||
| |||
|
Решение:
Метод «учета наименьших затрат» означает, что поставка всегда осуществляется в клетку с наименьшим тарифом. Первоначально поставку осуществляем в клетку с номером 
c наименьшим значением тарифа, равным 1: выбираем наименьшее значение между мощностью поставщика и потребностью потребителя, то есть 
Первому потребителю больше везти не требуется, поэтому остальные клетки в столбце будут пустые, а у поставщика осталось 14 – 10=4 единиц товара. Следующая клетка с номером 
(тариф равен 2): 
От первого поставщику больше перевезти нельзя, поэтому клетка 
пустая, у третьего потребителя осталось потребность в 7 – 5=2 единицы товара. Следующая клетка 
(тариф равен 3): 
клетка пустая, 12 – 4=8. Далее идет клетка 
(тариф равен 4): 
10 – 8=2. И последняя поставка осуществляется в клетку 
: 
Следовательно, первоначальное распределение будет иметь вид:
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Сетевое планирование и управление
Для сетевого графика, изображенного на рисунке,
критический путь имеет вид …
|
| 
| ||
| |||
| |||
|
Решение:
Выделим полные пути:
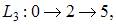
и вычислим их длины: 
Критическим путем называется наиболее продолжительный (по времени) полный путь, поэтому это путь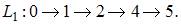 
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица выигрышей в игре с природой имеет вид:
Тогда средний выигрыш игрока по критерию Байеса относительно выигрышей будет равен …
|
| 4,65 | ||
| 3,8 | |||
| 3,65 |
Решение:
Определим предварительно неизвестную вероятность 
и вычислим средние выигрыши игрока:
Тогда наибольший средний выигрыш игрока будет равен 4,65.
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Транспортная задача
В транспортной задаче оптимальное распределение поставок имеет вид:
Тогда оптимальное значение целевой функции будет равно …
|
| |||
Решение:
Найдем предварительно значение тарифа 
Тогда значение целевой функции рассчитывается как сумма произведений тарифов на соответствующие объемы перевозок:
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Сетевое планирование и управление
Сетевой график изображен на рисунке
Тогда, для изменения критического пути, продолжительность работы можно увеличить на …
|
| 7 дней | ||
| 5 дней | |||
| 3 дня | |||
| 1 день |
Решение:
Выделим полные пути:
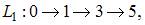
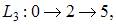
вычислим их длины: 
Тогда критическим будет путь 
с наибольшей длиной 
Чтобы критический путь изменился надо продолжительность работы увеличить, например, на 7 дней, так как 
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица выигрышей в игре с природой имеет вид:
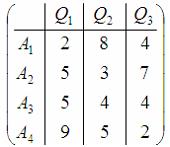
Тогда оптимальной по критерию Вальда будет стратегия …
|
|
| ||
|
| |||
|
| |||
|
Решение:
По критерию Вальда оптимальной является стратегия, которой соответствует максимальный из минимальных выигрышей, то есть 
Следовательно, оптимальной по критерию Вальда будет стратегия 