Р Е Ш Е Н И Е З А Д А Ч П О Ф И З И К Е
ЧАСТЬ 3
ОПТИКА. АТОМНАЯ ФИЗИКА. КВАНТОВАЯ МЕХАНИКА.
ЯДЕРНАЯ ФИЗИКА
Методические указания для заочников
Тверь 2016
УДК 53(075.8)
ББК 22.3я7
Предназначен для студентов первого курса заочного отделения ИДПО, а также для студентов дневного отделения факультетов ПИЭ, ИТ и ХТ. Содержит примеры решения и условия задач, предлагаемых при выполнении контрольных работ, необходимые справочные данные и список рекомендуемой литературы.
Обсужден и рекомендован к печати на заседании кафедры общей физики (протокол № от 2016 г.)
Составители: Испирян С.Р., Кривенко И.В.
© Тверской государственный
технический университет, 2012
Волновая оптика
1. В волновой оптике рассматривают свет как электромагнитную волну. Скорость распространения электромагнитной волны u зависит от диэлектрических и магнитных свойств среды. В вакууме u = c = 3·108 м/с. В среде с абсолютным показателем преломления n свет распространяется со скоростью
.
Для воздуха абсолютный показатель преломления 
; для других прозрачных сред 
. Скорость связана с длиной волны l и частотой n соотношением
.
При переходе света из среды с показателем преломления n 1 в среду с показателем преломления n 2 (на рис. 67 n 1 < n 2) выполняются законы − отражения
;
− преломления
,
где a – угол падения; b – угол отражения; g – угол преломления (все углы отсчитываются не от поверхности раздела сред, а от нормали к ней!).
Примерный диапазон длин волн (в вакууме), соответствующий видимому свету, включает значения от 0,40 мкм (фиолетовый свет) до 0,76 мкм (красный свет). Непосредственно примыкающий к видимому свету диапазон больших длин волн (λ > 0,76 мкм) относится к инфракрасной области, а меньших длин волн (λ < 0,38 мкм) – к ультрафиолетовой области.
Световая волна, в которой происходят колебания одной строго определенной частоты (соответственно, имеющая одну длину волны), называется монохроматической. В немонохроматической волне присутствуют колебания различных частот (предельный случай – белый свет, содержащий все частоты видимого диапазона).
2. Интерференция света – это явление перераспределения световой энергии в пространстве в результате наложения когерентных(имеющих одинаковую частоту и постоянную во времени разность фаз) световых волн. При этом в одних точках пространства возникают колебания с максимальной амплитудой (имеет место максимальная интенсивность) – освещенные участки, а в других – с минимальной амплитудой (минимум интенсивности) – темные участки. Если свет не является монохроматическим, интерференционная картина становится цветной, содержащей различные линии спектра.
Если один луч проходит путь длиной l1 в среде с показателем преломления n1, а другой луч – путь l2 в среде с показателем преломления n2, то оптическая разность хода этих лучей
.
Для светлых точек картины должно соблюдаться условие максимума
D = k×l,
для темных точек – условие минимума
,
где k = 0, 1, 2,... – целое число.
3. Дифракцией света называется огибание светом препятствий, размер которых соизмерим с длиной световой волны λ. При этом на экране за препятствием наблюдается картина, состоящая из максимумов и минимумов, т.е. освещенных и темных участков.
Одним из возможных препятствий для получения дифракционной картины является длинная узкая щель.
При прохождении через щель шириной b нормально падающей на нее плоской световой волны на экране Э за щелью наблюдается картина, состоящая из светлых и темных полос (максимумов и миниму-мов освещенности).
В центре картины (точка О) наблюдается самая яркая освещенная полоса (централь-ный максимум), далее темные полосы – первые минимумы, затем светлые полосы – первые максимумы, затем вторые минимумы и так далее.
Условие, при котором в произвольной точке М экрана наблюдается минимум:
где b – ширина щели, φ – угол между нормалью к щели и направлением на точку М (угол дифракции), m = 1, 2, 3... – номер минимума, λ – длина волны излучения.
Условие, при котором в точке М экрана наблюдается максимум:
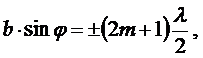
где m = 1, 2, 3... – номер максимума.
Другим препятствием, на котором можно наблюдать дифракцию света, является дифракционная решетка.
Дифракционная решетка представ-ляет собой пластинку с множеством параллельных узких щелей одинаковой ширины b, находящихся на расстоянии d друг от друга (см. рис.). Расстояние между центрами соседних щелей d называется постоянной (или периодом) дифракционной решетки.
Дифракционная картина на экране после дифракционной решетки представляет собой ряд освещенных пятен – главных максимумов. Углы, под которыми наблюдаются главные максимумы, находят из формулы:
.
Число k называется порядком главного максимума. k = 0, 1, 2,... – целое число.
Если дифракционную решетку облучать белым светом или светом сложного состава с различными длинами волн, то максимумы от каждой длины волны получаются на экране в разных местах, т.е. после решетки будет видна цветная картина, состоящая из нескольких спектров. Таким образом, дифракционные решетки используют для исследования света по спектральному составу.
Пример 1.
Луч света падает из воздуха на границу раздела с веществом, в котором скорость света u = 1,5·108 м/с. Определить отношение синуса угла падения к синусу угла преломления.
Решение:
По закону преломления 
. Абсолютный показатель преломления вещества 
; показатель преломления воздуха . Тогда 
.
Пример 2.
От двух когерентных источников S1 и S2 на экран падает свет с длиной волны λ = 0,8 мкм. На экране наблюдается интерференционная картина, причем в точке М находится светлое пятно. Когда на пути одного из лучей перпендикулярно к нему поместили мыльную пленку с показателем преломления n = 1,33, в точке М образовалось темное пятно. Какова минимальная толщина пленки?
Решение:
До внесения пленки в точке М наблюдается интерференционный максимум, т.е. разность хода лучей от источников D1 = l1 – l2 = k1×l, где k1 – целое число.
После внесения пленки максимум меняется на минимум, т.к. из-за того, что часть второго луча проходит в среде с показателем преломления n = 1,33, изменяется 
оптическая разность хода лучей. Оптическая длина пути второго луча в этом случае 
. Тогда разность хода 
, где k2 – целое число.
Найдем разницу разностей хода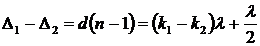 
. Толщина пленки будет минимальная, если 
. Тогда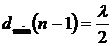 
. Следовательно, 
.
Пример 3.
Дифракционная решетка длиной l = 5 мм имеет N = 2000 штрихов. Сколько линий (главных максимумов) будет содержать спектр, образующийся при нормальном падении на нее плоской монохроматической волны длиной λ = 420 нм?
Решение:
Согласно условию главного максимума дифракционной решетки , где k = 0, 1, 2,... – порядковый номер максимума. Период дифракционной решетки d – это расстояние между ее штрихами, тогда 
. Угол, под которым можно наблюдать максимумы после дифракционной решетки, может изменяться от 0 до 900. Тогда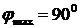 
и
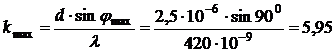
Т. к. порядок максимума может быть только целым числом, то 
. Причем округление следует проводить только в меньшую сторону, т.к. больше, чем 900 угол отклонения лучей на решетке быть не может.
Помимо этого следует учесть еще и центральный максимум, для которого 
, а также то, что дифракционная картина является симметричной и по другую сторону от центрального максимума наблюдается еще пять.
Таким образом, общее число главных максимумов, которые содержит спектр данной дифракционной решетки 
.
Тепловое излучение и давление света
1.Испускание электромагнитных волн нагретыми телами, происходящее за счет их внутренней энергии, называется тепловым излучением. Основные характеристики источников теплового излучения:
− Энергетический поток Ф – энергия W, излучаемая (передаваемая, поглощаемая, отражаемая, пропускаемая) за единицу времени:
, [ Вт ].
− Средний энергетический поток за промежуток времени Δt
.
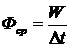− Излучательность (энергетическая светимость) R – энергия, излучаемая за единицу времени единицей площади поверхности тела во всем диапазоне длин волн (от 0 до ¥). При равномерной плотности излучения
, [ 
].
− Спектральная плотность энергетической светимости (спектральная излучательная способность)
, [ 
].
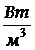где dRl – энергия, излучаемая за единицу времени с единицы площади поверхности в интервале длин волн от l до l + dl.
2. Характеристики приемника излучения (поверхности, на которую падает свет):
− Коэффициент отражения
,
где Фпад – падающий на поверхность тела энергетический поток; Фотр – часть этого потока, отраженная поверхностью. Для идеально зеркальной поверхности 
.
− Коэффициент пропускания
,
где Фпад – падающий на поверхность тела энергетический поток; Фпрош – часть этого потока, прошедшая сквозь поверхностью. Для непрозрачной поверхности 
.
− Спектральная поглощательная способность (коэффициент поглощения, степень черноты)
,
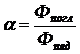где Фпад – падающий на тело энергетический поток; Фпогл – часть этого потока, поглощенная телом. Поглощательная способность тела зависит от его температуры и длины волны 
Тело, поглощающее весь падающий на него энергетический поток независимо от длины волны и температуры, называется абсолютно черным телом (АЧТ). Для АЧТ a = 1. Тело, у которого коэффициент поглощения не зависит от длины волны, называется серым. Для серого тела a = a (Т) и a ≠ a (λ).
Характеристики приемника излучения связаны соотношением 
.
3. Законы теплового излучения
− Закон Кирхгофа − отношение спектральной плотности излучательности к спектральной поглощательной способности не зависит от природы тела и является универсальной (одинаковой для всех тел) функцией длины волны и температуры:
.
− Закон Стефана – Больцмана – излучательность АЧТ прямо пропорциональна 4-ой степени абсолютной температуры тела:
,
где σ – постоянная Стефана – Больцмана.
С учетом закона Кирхгофа для серого тела 
.
− Закон Вина – длина волны lm , на которую приходится максимум излучения АЧТ, обратно пропорциональна его абсолютной температуре Т:
,
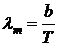где b – постоянная в законе Вина.
4. Давление, которое оказывает нормально падающий свет на поверхность
,
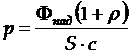где Фпад – падающий на поверхность тела энергетический поток; ρ – коэффициент отражения поверхности; S – площадь поверхности; с – скорость света в вакууме.
Т.к. свет представляет поток фотонов, то 
, где Nф – количество падающих на поверхность фотонов, 
– энергия фотона, Δt – время облучения.
Пример.
Поверхность Солнца имеет температуру Т = 6000 К. Считая Солнце абсолютно черным телом, определить энергию, излучаемую Солнцем с участка поверхности 1 мм2 за одну минуту, а также длину волны, на которую приходится максимум спектральной плотности энергетической светимости Солнца при данной температуре.
Решение:
Согласно закону Стефана-Больцмана, излучательность Солнца определяется как
Вт/м2
Величину энергии W можно найти по формуле
Дж.
Величину l найдем из условия задачи – она равна длине волны lmax, соответствующей максимуму энергии излучения Солнца.
Согласно закону смещения Вина
где b = 2,9×10-3м×К – постоянная Вина.
Таким образом 
Фотоны. Фотоэффект
1. Согласно представлениям квантовой теории энергия световых волн не только испускается, но и поглощается и переносится в пространстве отдельными порциями – квантами. Это позволяет рассматривать электромагнитное излучение как поток особых частиц – фотонов.
− Энергия фотона e прямо пропорциональна частоте излучения (обратно пропорциональна длине волны):
или 
,
где n – частота; λ – длина волны; с – скорость света в вакууме; h – постоянная Планка.
− Масса фотона может быть найдена из соотношения массы и энергии
.
Фотон может существовать, только если движется со скоростью света, в покое фотон не существует, следовательно, масса покоя фотона равна нулю.
− Импульс фотона
.
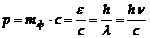2. Фотоэффект – явление выбивания электронов из металла фотонами. Превращение энергии при взаимодействии фотона излучения с электроном металла описывается уравнением Эйнштейна
,
где eф – энергия фотона; Ав – работа выхода электрона из металла; 
– максимальное значение кинетической энергии выбитого электрона. Работа выхода зависит от рода металла и состояния его поверхности. Она может быть найдена в справочных таблицах для соответствующего металла.
3. Если энергии фотона недостаточно для того, чтобы выбить электрон, фотоэффект не наблюдается. Минимальная частота излучения, при которой начинается фотоэффект, называется частотой красной границы nкр . Соответствующее значение максимальной длины волны называется длиной волны красной границы lкр .
, 
.
4. Если между катодом и анодом создать «обратное» электрическое поле, т.е. на катод подать «+», а на анод «−» (U < 0), то это поле будет возвращать электроны обратно к катоду. При разности потенциалов этого поля Uз, называемой запирающим (задерживающим) напряжением все выбитые электроны будут возвращаться обратно на катод.
Запирающее напряжение находится из соотношения:
,
где е – элементарный заряд (абсолютная величина заряда электрона).
5. При прямом напряжении (на катод «−», на анод «+») электроны, вылетающие с катода, летят на анод. Когда все выбитые светом при фотоэффекте электроны достигают анода, ток, протекающий в цепи (фототок) становится насыщенным и не зависит от приложенного напряжения. Фототок насыщения может быть найден по формуле
,
где Nэ – количество выбитых электронов, е – заряд электрона, Δt – время протекания тока.
Пример
Найти максимальную скорость фотоэлектронов, вылетающих с поверхности цезия при облучении его светом с длиной волны 0,5 мкм.
Решение:
Максимальную скорость фотоэлектронов можно найти из уравнения Эйнштейна для внешнего фотоэффекта , где максимальная кинетическая энергия электронов 
, me – масса электрона, vmax – максимальная скорость выбиваемых электронов; энергия фотона 
, 
Дж∙с – постоянная Планка, 
– частота падающего света.
Тогда 
.
Работа выхода электрона Ав зависит от природы металла. Из справочных таблиц найдем значение работы выхода для цезия 
.
Подставим значение частоты, работы выхода (предварительно выразив ее в Дж (1эВ = 1,6×10-19Дж)) и массы электрона (mе = 9,11×10-31 кг) в выражение скорости электронов:
Спектр атома водорода
1. Атом водорода состоит из положительно заряженного ядра, имеющего малые по сравнения с диаметром атома размеры и массу, практически равную массе атома, вокруг которого движется по замкнутым орбитам электрон. В основе теории атома водорода Н. Бора лежат два постулата:
1) электрон в атоме водорода может находиться не на любых, а на строго определенных – стационарных орбитах, которые имеют определенные (дискретные) радиусы и которым соответствуют определенные (дискретные) значения энергии; находясь на стационарных орбитах, электрон не излучает и не поглощает энергию;
2) при переходах с одной стационарной орбиты с номером k на другую с номером n электрон излучает или поглощает энергию в виде квантов света:
,
где Еn и Еk – энергии электрона на n -той и k -той стационарных орбитах, соответственно. k и n – номера орбит (натуральные числа). Если k > n, то атом излучает квант света, если k < n, атом поглощает квант света.
2. Энергия электрона на стационарной орбите обратно пропорциональна квадрату номера орбиты
,
где Е 1 – энергия на первом уровне,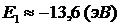 
.
3. Формула Бальмера определяет длину волны света, излучаемого или поглощаемого атомом при переходе электрона из одного стационарного состояния в другое
,
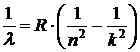где l – длина волны; R – постоянная Ридберга; k и n – номера орбит (натуральные числа).
Частоту можно найти по формуле 
, где с – скорость света в вакууме.
4. Спектр испускания атома водорода имеет линейчатый характер, т. е. состоит из отдельных линий, группирующихся в серии. Число n в формуле Бальмера определяет серию в спектре излучения. Значение n = 1 соответствует ультрафиолетовой серии Лаймана, n = 2 – видимой серии Бальмера, n = 3 – инфракрасной серии Пашена; значения n > 3 также соответствуют сериям, лежащим в инфракрасной области. Число k в формуле Бальмера (k > n) – определяет конкретную линию в данной серии. Переходы, соответствующие разным сериям, изображены на энергетической диаграмме на рис.
 |
Пример.
Переходя из одного возбужденного состояния в другое, атом водорода испустил фотон с длиной волны 102,5 нм. С какой орбиты на какую перешел электрон в атоме?
Решение
Т.к. заданная длина волны λ = 102,5 нм лежит в ультрафиолетовой области, то, следовательно, данный переход принадлежит серии Лаймана, для которой число n = 1, что соответствует переходу электрона на основной уровень.
Для определения номера энергетического уровня, с которого перешел электрон, воспользуемся формулой Бальмера. Положив в ней n = 1, найдем число k:
;
;
поскольку k – целое число, принимаем k = 3.