Пусть G – конечная мультипликативная абелева группа порядка h. Рассмотрим сумму:
S =  ,
,
где А пробегает все элементы G, и сумму
Т = 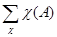
где c пробегает все элементы группы характеров Ĝ.
Рассмотрим чему равна каждая из сумм.
а) Если В-фиксированный элемент группы G и А пробегает все элементы G, то АВ также пробегает все элементы группы G. Следовательно,
S·c (В) = 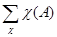 c (В) =
c (В) =  =
=  = S.
= S.
Получили Sc (В) = S, откуда следует, что (c (В) – 1)·S = 0. Следовательно, возможны два варианта:
1) S = 0, то c (В) – негативный характер
2) S≠0, то c (В) = 1 для каждого элемента В?G и в этом случае c (В)= c1(В) есть главный характер и сумма S равна порядку h группы G. Таким образом,
S =  = {
= {  (1.2)
(1.2)
б) Если мы умножим сумму Т на некоторый характер c’ группы Ĝ, то аналогичным образом получим
c’ (А) Т = 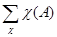 c’ (А) =
c’ (А) =  = Т,
= Т,
Следовательно,
1) или Т = 0, то А ≠Е
2) или Т ≠ 0, то c’ (А) = 1 для каждого характера c’? G. В этом случае согласно свойству 3§ 1, имеем А=Е. И тогда Т=h. Таким образом,
Т =  = {
= { 
Характеры Дирихле
Пусть m – положительное целое число. Определим числовые характеры по модулю m. Мы знаем, что j(m) приведенных классов вычетов по модулю m образуют мультипликативную абелеву группу порядка h=j(m). Мы можем, следовательно, рассмотреть характер этой группы. Но определение характера для приведенных классов вычета по модулю m можно перенести на множество целых чисел следующим образом. Положим
c(а)= c(А), если аÎА,
где А – приведенный класс вычетов по модулю m. Тогда очевидно, c(а)= c(b) (mod m), и c(ab)= c(а) c(b), если (а, m)=(b, m)=1. Поскольку c(А)¹0 для каждого приведенного класса вычетов А, то c(а)¹0, если (a, m)=1.
Это определение применимо только к целым числам а, которые взаимно просты с m.
Мы можем рассмотреть его на все целые числа, положив
c(а)=0, если (a, m)>1.
Следовательно, характер по модулю m есть арифметическая функция c, обладающая следующими свойствами:
c(а)= c(b), если с=b (mod m)
c(ab)= c(a) c(b) для всех целых a и b
c(а)=0, если (a, m)>1
c(а)¹0, если (a, m)=1
Имеется точно j(m) – количество характеров по модулю m, где j(m) – количество положительных целых чисел, не превосходящих m и взаимно простых с m. Они образуют мультипликативную абелеву группу приведенных классов вычета по mod m. Единичным элементом этой группы будет главный характер c1, то есть такой характер, что c1(а)=1, если (а, m)=1. Далее имеем следующее соотношение ортогональности:
 = {
= { 
 = {
= { 
Пусть m – положительное целое число. Определим числовые характеры по модулю m. Комплекснозначная функция, определенная для всех целых чисел n, называется числовым характером или характером Дирихле по модулю m, она удовлетворяет следующим условиям:
а) c (n) = 0 тогда и только тогда, когда (n, m) ≠ 1
б) c (n) периодична с периодом m
в) для любых чисел а и b
c (аb) = c (а) c (b)
Функция
c1(n) = { 
является числовым характером и называется главным характером. Остальные числовые характеры по модулю m называются неглавными.
Имеет место следующее утверждение о числовых характерах.
Теорема 1 Существует равно φ(m) числовых характеров по модулю m. Если c = c (n) – числовой характер по модулю m, то:
1) для n, взаимно простых с модулем m, значения c (n) есть корень из 1 степени φ(m).
2) для всех n выполняется неравенство /c (n)/ ≤1
3) Имеет место равенство
 {
{ 
4) Для каждого целого числа n
 = {
= { 
Доказательство. Пусть c (n) – некоторый числовой характер по модулю m. Из пункта б) определения следует, что c (n) задает некоторую функцию c’( ) = c (n) на мультипликативной группе
) = c (n) на мультипликативной группе  классов вычетов по модулю m, взаимно простых с m, а именно
классов вычетов по модулю m, взаимно простых с m, а именно
c’( ) = c (n)
) = c (n)
Здесь  обозначает класс вычетов по модулю m, содержащий n. Так как c(1) ≠ 0, то c’(
обозначает класс вычетов по модулю m, содержащий n. Так как c(1) ≠ 0, то c’( ) не равняется тождественно нулю, а из пункта в) определения числового характера следует, что c’(
) не равняется тождественно нулю, а из пункта в) определения числового характера следует, что c’(
 ) = c’(
) = c’(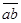 ) = c’ (ab) = c (a) c (b) = c’(
) = c’ (ab) = c (a) c (b) = c’( )c’(
)c’( ).
).
Таким образом, c’( ) есть характер модультипликативной группы Gm.
) есть характер модультипликативной группы Gm.
Обратно, по каждому характеру c’( ) группы Gm можно построить числовой характер c (n) по модулю m, положив
) группы Gm можно построить числовой характер c (n) по модулю m, положив
 {
{ 
Установленное соответствие является взаимнооднозначным. И все утверждения теоремы 1 следуют из доказанного выше для групповых характеров применительно к группе Gm, если учесть, что порядок группы Gm равен φ(m), где φ(m) – функция Эйлера.
В дальнейшем требуется еще одно утверждение с числовых характерах. Обозначим для каждого c, c ≥ 1

Где суммирование ведется по всем натуральным числам n, не превосходящим c.
Лемма 2. Пусть c (n) – неглавный характер. Тогда для каждого c, c ≥ 1 справедливо неравенство
/S(x)/<m
Доказательство. Функция c (n) периодична с периодом m и по теореме з
 0, так как c≠ c1
0, так как c≠ c1
Поэтому, представив [c] – целую часть числа c – в виде [c]=m1+z, 0£z£m, будет иметь
S(c) =S([c])=q 

В виду равенства /c(n)/£1 отсюда получили S(c)£z£m
L-функция Дирихле
Пусть х(п) – произвольный характер по модулю m. Рассмотрим ряд
 , (2.1)
, (2.1)
члены которого являются функциями комплексного переменного S. В области сходимости он определяет функцию, которая называется L-функцией Дирихле, соответствующей характеру c(n), и обозначается L (s, c).
Лемма 3
1. Если c¹c1, то ряд (1) сходится в области ReS > 0 и определяемая им функция L (s, c) является аналитической в этой области.
2. Ряд, определяющий L (S, c1), сходится в области ReS >1. Функция L (S, c1) является аналитической в области ReS > 1.
Доказательство.
Пусть c(n) – произвольный характер по модулю m, а б – некоторое положительное число. Так как /c(n)/ £ 1, то в области ReS > 1 + б справедливо неравенство

Следовательно, ряд (1) равномерно сходится в области ReS > 1 + б. Определяемая им функция L (S, c) по теореме Вейерштрасса о сумме равномерно сходящегося ряда аналитических функций является аналитической в этой области. Ввиду произвольности 6 это доказывает второе утверждение Леммы.
Для неглавных характеров c(n) потребуется более сложное исследование ряда (1).
Лемма 4 (преобразование Абеля).
Пусть an, n=1,2,…, – последовательность комплексных чисел, c>1,
А(c)= 
а q(t) – комплекснозначная функция, непрерывно дифференцируемая на множестве 1£t£¥
Тогда
 (2.2)
(2.2)
Если же
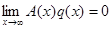
то
 (2.3)
(2.3)
при условии, что ряд в левой части равенства сходится.
Доказательство. Положим А(0)=0 и В(х) равным левой части равенства (2.2). Тогда при любом натуральном N

так как А(0)=0. Далее

поскольку функция А(х) постоянна на каждом полуинтервале n£t<n+1. Следовательно, равенство (2.2) доказано при целых значениях х.
пусть х³1 – произвольное число. Положим N=[x]; значит, N£x£N+1. Тогда А(х)=А(N), B(x)=B(N), а

Следовательно,
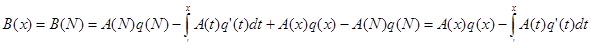
Тем самым доказано, что равенство (2.2) верно и для нецелых чисел значений х.
Равенство (2.3) получаем из равенства (2.2) переходом к пределу при х®¥. Лемма доказана.
Воспользовавшись леммой 4, получим следующее равенство
 (2.4)
(2.4)
где

функция, введенная Лемме 4.
Для s = p+it из области ReS = s, где s – некоторое положительное число, пользуясь леммой 4, находим

Поэтому интеграл

сходится в области ReS > s. Поскольку в этой области выполняется неравенство

то из равенства (2) следует, что ряд (1), определяющий функцию L (S, x), сходится в области ReS > s. Эти рассуждения справедливы для любого положительного числа s. Значит, ряд (1) сходится в полуплоскости ReS > 0.
Из равенства (2) следует, что в этой полуплоскости для L-функции, соответствующей неглавному характеру c(n), справедливо представление

 (2.5)
(2.5)
так как

Интеграл, стоящий в правой части равенства (2.5), можно также представить в виде
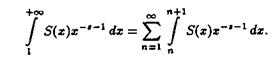 (2.6)
(2.6)
Члены ряда (2.6) являются аналитическими функциями в области ReS >s, что следует из равенств
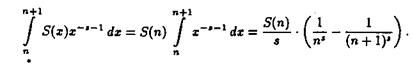
При этом использовано, что на полуинтервале n£х< n+1 функция S(х) принимает значение S(n). Поскольку

то ряд (2.6) равномерно сходится в области ReS >s. Отсюда, как и выше, получаем, что сумма его, т.е.

является аналитической функцией (по теореме Вейерштраса) в области ReS >s.
Из представления (2.5) следует теперь, что L (S, x) есть аналитическая функция в полуплоскости ReS >s, а ввиду произвольности S – s и b полуплоскости ReS > 0.
Следствие. Пусть c (n) – произвольный характер. Тогда в области ReS > 1 справедливо равенство
 (2.7)
(2.7)
Это следует из того, что ряд (2.1) по доказанному равномерию сходится в области ReS>1+s, где s>0. Следовательно, по теореме Вейштрасса о равномерно сходящихся рядах аналитических функций в этой области ряд (2.1) можно почленно дифференцировать

Поэтому в полуплоскости ReS>1+s выполняется равенство (2.7). Так как в этом рассуждении s-любое положительное число, то равенство (2.7) будет справедливо в полуплоскости ReS>1.
Для L-функций имеет место представление в виде бесконечного произведения по простым числам, аналогичное тождеству Эйлера. Рассмотрим вспомогательную Лемму.
Лемма 5. Пусть функция f(n) вполне мультипликативна и ряд
 (2.8)
(2.8)
абсолютно сходится. Тогда выполняется равенство
 (2.9)
(2.9)
Доказательство. Отметим прежде всего, что /f(n)/<1 при любом натуральном n>1. В противном случае при каждом mÎN
/f(n)m/=/f(n)/m³1,
что противоречит сходимости ряда (2.6). Поэтому при каждом простом р ряд

абсолютно сходится, и его сумма как сумма бесконечно убивающей геометрической прогрессии равна (1-f(р))-1. Кроме этого, в силу абсолютной сходимости, ряды можно перемножить. Перемножая конечное число таких рядов и используя то, что f(n) есть вполне мультипликативная функция, получим
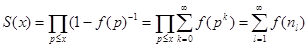
где ne = pa … pas и в сумме в правой части равенства содержатся такие и только такие слагаемые f(ne), что все просты делители ne не превосходят х. Следовательно, в разности

остаются те и только те слагаемые f(me), для которых у числа me имеется хотя бы один простой делитель р>x. Тогда оценим разность
/S-S(x)/£ 
и из абсолютной сходимости ряда (2.8) следует, что

Это доказывает, что бесконечное произведение (2.7) сходится и выполняется утверждение Леммы.
Лемма 6. Для каждого характера c(n) в области ReS > 1 справедливо представление

Доказательство. Эта лемма является следствием Леммы 5, поскольку функция c(n) вполне мультипликативна, то есть c(АВ)= c(А) c(В), и выполняется неравенство /c(n)/£ 1 по теореме 1.
Следствие 1. В области ReS > 1 для главного характера c1(n) по модулю m справедливо равенство
 (2.10)
(2.10)
и поэтому функция L (S, c1) может быть аналитически продолжена в область ReS > 0, где она имеет единственный полюс (первого порядка) в точке S=1.
Действительно, по определению главного характера c1(n) имеет место равенство

Поэтому

Пользуясь теперь тождеством Эйлера для дзета-функции Римана получаем равенство (2.10). Остальные утверждения легко следуют из этого равенства, поскольку дзета-функция является аналитической в области ReS > 0 с единственным полюсом первого порядка в точке S = 1.
Следствие 2. Для каждого характера c функция L (S, x) не обращается в нуль в области ReS > 1.
Доказательство.
Если s = ReS > 1. то

Пользуясь неравенством для дзета-функции Римана, находим

Получаем:
L (S,c) ≥ 
 > 0
> 0
Теперь докажем утверждения, что L – функция, соответствующая неглавному характеру c, точке S =1 отлична от нуля.
Теорема 2. Если c – неглавный характер, то L (1, c)≠0
Для доказательства рассмотрим 2 случая
1. Пусть характер c – комплексное число, не является действительным. Тогда характер c2(n) не является главным. В этом случае доказательство теоремы будет основываться на тех же идеях, что и доказательство отсутствия нулей дзета – функции на прямой ReS=1.
Лемма7. Пусть 0< ч< 1, а х – действительное число, тогда выполняется неравенство /(1 – ч)3 (1 – чеix)4 (1 – че2ix)/-1 ≥ 1
Доказательство.
Для всех z из круга /z/<1 имеет место расположение
– ln (1 – z) = 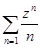 (2.11)
(2.11)
Так как ln(t) = Re lnt, то обозначая М (ч φ), левую часть неравенства (2.11), получим
lnM (ч φ) = 3ln (1 – ч) – 4 ln (1 – чеi4) – ln (1 – че2i4) = – 3ln (1- ч) – 4Reln/1 – чеi4 / – Reln/1 – че2i4 /= 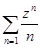 rc (3+4e)inl /1-rei4/=
rc (3+4e)inl /1-rei4/= 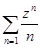 (3+4cosnl+2cos2nl)=
(3+4cosnl+2cos2nl)=  (2+4cosa+1+cos2a)=
(2+4cosa+1+cos2a)= 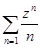 1 (1+cosa)2³0
1 (1+cosa)2³0
ln=M (r, l)=³0
Следовательно, M (r, l)=³1 доказана.
Из леммы 7 следует, сто при любом действительном S>1 выполняется равенство:
|L3(8, c 1) L4(S, c ) 4 (S, c 4) 1 = П (1-  )3(1-
)3(1- 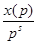 )4(1-
)4(1-  )|-1 (2.12)
)|-1 (2.12)
Получая в лемме ч = р -s, т.е.
0< ч = c 1(р) <1
0< р -s <1
c (р) р-s = чеi4, в силу того что c (р) – комплексное
c (р) р-s = че2i4
Получаем, что каждый сомножитель в правой части равенства (f) не меньше 1 и, следовательно, при любом S>1 выполняется равенство:
|L3(Sc1) · L4(Sc) L (Sc2)| ≥ 1 (2.13)
Допустим, что для некоторого характера c (c2≠c1) выполняется равенство
L (1, c) = 0 (2.14)
Оценим сверху левую часть неравенства. Из оценки дзета-функции Римана
ξ(S) ≤  , следует, что при S? R, S>1 выполняется неравенство
, следует, что при S? R, S>1 выполняется неравенство
а) 0 < 4 (S, c1) = 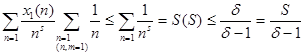
получили 0<L (S, c1)≤ 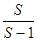
б) Функция L (S, c) разложим в ряд Тейлора
L (S, c) = Cp + C1 (S – 1) + C2(S – 1)2 +… + Cn(S – 1)n +…
Предположим, что у нее есть нуль L (1, c) = 1; тогда С0 = 0
Перепишем разложение L – функции в ряд
L(Sc) = Cк (S – 1)к + Ск+1(S – 1)к+1 = (S – 1)1 (Cк + Ск+1(S -1) +….), где к≥1, Ск ≤ 0, т. к. S>1
| L (S, c)| = |S – 1|k| Ck + Ck+1(S – 1) +….| ≤ 2 Ck|S – 1)k, при |S – | < r
Функция L (S, c2) в точке S = 1 не имеет полюса, следовательно не имеет особенности. Это в силу того, что c комплексное и c2≠c1
Получаем неравенство:
L (S, c2) ≤ C,
При условии | S – 1|< δ
Учитывая все неравенства и оценки
| L3 (S, c) L4(S, c) L (S, c2)| = (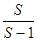 )3 · 24 |Ck|4 (S – 1)4k· C≥1
)3 · 24 |Ck|4 (S – 1)4k· C≥1
Следовательно, это неравенство становится противоречивым, если перейти к пределу при S→1+0. Полученное противоречие показывает, что равенство (2.14) не выполняется.
2. Рассмотрим c – вещественный характер, т.е. принимающий только вещественные значения, несовпадающий с главным характером
Лемма 8. Пусть c – вещественный характер.
Рассмотрим функцию
F(S) = ξ(S) L (S, x) (2.15)
Докажем, что если Re S>1, то
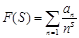 (2.16)
(2.16)
представляется рядом Дирихле, которого справедливы следующие утверждения:
1) Все коэффициенты аn ≥ 0
2) при n=k2, k? / N(N)/ аn ≥1
3) В области ReS<1 можно почленно дифференцировать, то есть
F (k) (S)= 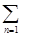 (-1)k(ln n)k
(-1)k(ln n)k 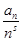 k=1,2…; (2.17)
k=1,2…; (2.17)
4) Ряд (1) в точке S=1/2 расходится.
Доказательство. В области ReS > 1 ряды, определяющие функции S(S) и L (S,c), абсолютно сходятся, поэтому их можно перемножить:
где
 (2.19)
(2.19)
Пусть 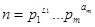 - расположение числа n в произведение простых сомножителей. Тогда все натуральные делители l числа n имеют вид
- расположение числа n в произведение простых сомножителей. Тогда все натуральные делители l числа n имеют вид
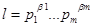

поэтому из равенства (14) находим, что

где ani = 1+ c (pi)+ … +cLi (pi), i=1,…, m (2.21)
так как c – вещественный характер, то он может принимать только три значения: 0, 1, -1. Из равенства (2.21) следует, что
 (2.22)
(2.22)
Во всех случаях числа ani³0, а значит, и an=an1 … anm³0
Если же число п является полным квадратом, то
N=k2=p/2g … pm 2g,
и из равенств (2.20) и (2.22) следует, что аn ³1
При любом s > 0 в области ReS> 1 +s выполняется неравенство

Ряд (2.18) сходится в области ReS > 1. Поэтому по признаку Вейерштрасса ряд (2.16) сходится равномерно в области ReS > 1 + s, а по теореме Вейерштрасса его можно в этой области почленно дифференцировать любое число раз. Следовательно, в области ReS > 1 +s выполняется равенство (2. 17), а в силу произвольности s оно выполняется и в области ReS > 1.
Однако ряд (39) расходится, так как по второму утверждению леммы
Ряд (2.16) при S =  имеет неотрицательные члены. Поэтому, если бы он сходился, то также сходился бы ряд
имеет неотрицательные члены. Поэтому, если бы он сходился, то также сходился бы ряд
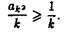 (2.23)
(2.23)
Следовательно, ряд (2.23) расходится. Лемма доказана.
Переходим непоредственно к доказательству второго случая теоремы. Допустим, что L (1,c) = 0. Тогда полюс дзета-функции будет компенсироваться в произведении S(S) L (S, c) нулем функции L (S, c).
Поэтому функция (2.15) F(S) будет аналитической в области ReS > 0 так как в точке S=1 у F(z) – устраненная особая точка. Следовательно, ее можно разложить в ряд Тейлора в точке S = 2:
 (2. 24)
(2. 24)
радиус сходимости которого не меньше 2 R³2/
Из равенств (2.17), в частности S=2, находим
 (2.25)
(2.25)
В радиусе сходимости будет брать не все S, а только вещественные ReS=s S=sÎ(0,2). Пользуясь разложениями (18) и (19), находим

Члены двойного ряда неотрицательны, поэтому он сходится абсолютно, и в нем можно поменять порядок суммирования. Тогда

Следовательно, ряд (2.16) сходится во всех точках, s < (, 0, 2), и в точке  , а это противоречит четвертому утверждению леммы. Поэтому L (S,c)¹0/
, а это противоречит четвертому утверждению леммы. Поэтому L (S,c)¹0/
Этим завершается доказательство теоремы
По следствию 2 леммы 2 функция  является аналитической в области ReS > 1. Для дальнейшего доказательства теоремы Дирихле нам будет необходимо представление этой функции в виде ряда, аналогичного ряда (2.16).
является аналитической в области ReS > 1. Для дальнейшего доказательства теоремы Дирихле нам будет необходимо представление этой функции в виде ряда, аналогичного ряда (2.16).
Лемма. Для каждого характера c(n) в области ReS > 1 справедливо равенство
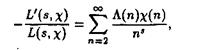 (2.26)
(2.26)

Доказательство.
Так как S=s+it имеет место неравенство

получаем, что ряд стоящий в правой части равенства (2.26), абсолютно сходится в области s>1. Умножим этот ряд на ряд определяющий L (S, c). Получили

Предпоследнее равенство имеет место ввиду равенства  ), а последнее – по следствию из леммы 3, равенство 2.7.
), а последнее – по следствию из леммы 3, равенство 2.7.