Как ни странно, но самым простым и одним из самых эффективных (при правильном использовании) алгоритмов шифрования является так называемое XOR-шифрование. Попробуем рассмотреть идею этого наипростейшего метода.
Как известно из булевой алгебры, операция логического сложения « » по модулю 2 (или логического исключаещего ИЛИ — XOR, eXclusive OR) имеет следующую семантику:
» по модулю 2 (или логического исключаещего ИЛИ — XOR, eXclusive OR) имеет следующую семантику:
таблица истинности для OR:
| xi | yi | xi  yi yi
|
таблица истинности для XOR:
| xi | yi | xi  yi yi
|
то есть:
| x | = | |

| ||
| y | = | |
| z | = |
То есть, операция z = x  y по сути поразрядная (побитовая — результат не зависит от соседних битов). Если только один из соответствующих битов равен 1, то результат 1. А если оба 0 или оба 1, то результат 0. Если внимательно посмотреть на результат применения XOR к двум двоичным числам, то можно заметить, что мы можем восстановить одно из слагаемых при помощи второго: x = z
y по сути поразрядная (побитовая — результат не зависит от соседних битов). Если только один из соответствующих битов равен 1, то результат 1. А если оба 0 или оба 1, то результат 0. Если внимательно посмотреть на результат применения XOR к двум двоичным числам, то можно заметить, что мы можем восстановить одно из слагаемых при помощи второго: x = z  y или y = z
y или y = z  x.
x.
Отсюда можно сделать следующие выводы: зная число y и применяя XOR к x, мы получим z. Затем, мы, опять же используя y, получим из z обратно число x. Таким образом мы можем преобразовать последовательность чисел (x)i в последовательность (z)i. Теперь мы можем назвать число y кодирующим (или шифрующим) ключом. Данное криптографическое преобразование можно описать следующим отношением:
(z)i=(x)i  у.
у.
Тут (z)i = шифротекст, а (x)i – соответствующий ему открытый текст.
Дешифрование шифротекста по известному ключу у согласно описанным свойствам операции XOR производится следующим образом:
(x)i=(z)i  у.
у.
Если человек не знает ключа, то он не сможет восстановить исходную последовательность чисел (x)i. Но если (x) i являются байтовым представлением букв текста, то опытный пользователь сможет вскрыть зашифрованный текст. Поскольку каждая буква будет представлена в шифротексте одним и тем же кодом z, то воспользуясь частотным словарем взломщик сможет вычислить шифрующий ключ y, если у него будет в распряжениии достаточно длинный шифротекст.
|
|
В свете последних рассуждений приходим к мысли, что напрямую кодировать простой текст нельзя. Во-первых, число, представляющее пробел, будет по-прежнему разделять слова и в шифротекте. Выделив это часто встречающееся одно и то же число, пользователь догадается, что это закодированный пробел. Во-вторых, короткие часто встречающиеся предлоги и союзы также помогут взломщику в определении ключа. Поэтому самым эффективным способом является использование длинного ключа, покрывающего несколько букв, а лучше равного по длине самому сообщению. Так, если мы кодируем достаточно длинное сообщение (не менее 5-10 предложений) с помощью случайного ключа такой же длины, то такое сообщение очень сложно расшифровать. Еще более высоких результатов по надежности можно достичь, если перед шифрованием произвести, например, сжатие текста каким-либо архиватором. Плюс к тому же, если сообщение имеет малую длину, можно добавить в начало и конец сообщения случайные последовательности символов.
Моноалфавитные шифры
Метод простой подстановки
Метод простой подстановки предполагает, что в соответствие каждому символу открытого текста ставится произвольный символ из того же алфавита.
|
|
| Открытый текст: | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| Шифро-ванный текст: | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
Если в строке "Шифрованный текст" допустить использование любой из перестановок 26 символов алфавита, то мы получим 26!, или более чем 4×1026 возможных ключей. Это на 10 порядков больше, чем размер пространства ключей DES, и это кажется достаточным для того, чтобы сделать невозможным успешное применение криптоанализа на основе метода последовательного перебора.
Однако для криптоаналитика существует и другая линия атаки. Если криптоаналитик имеет представление о природе открытого текста (например, о том, что это несжатый текст на английском языке), можно использовать известную информацию о характерных признаках, присущих текстам на соответствующем языке. Чтобы показать, как этот подход применяется на практике, рассмотрим небольшой пример.
UZQSOVUOHXMOPVGPOZPEVSGZWSZOPFPESXUDBMETSXAIZVUEPHZHMDZSHZOWSFPAPPDTSVPQUZWYMXUZUHSX EPYEPOPDZSZUFPOMBZWPFUPZHMDJUDTMOHMQ
На первом этапе можно определить относительную частоту появления в тексте различных букв и сравнить их со среднестатистическими данными для букв английского языка, показанными на рис. 1.
Если сообщение достаточно длинное, этой методики уже может быть достаточно для распознавания текста, но в нашем случае, когда сообщение небольшое, точного соответствия ожидать не приходится. В нашем случае относительная частота вхождения букв в шифрованном тексте (в процентах) оказывается следующей.
| P | 13,33 | H | 5,83 | F | 3,33 | В | 1,67 | С | 0,00 |
| Z | 11,67 | D | 5,00 | W | 3,33 | G | 1,67 | К | 0,00 |
| S | 8,33 | Е | 5,00 | Q | 2,50 | Y | 1,67 | L | 0,00 |
| U | 8,33 | V | 4,17 | T | 2,50 | I | 0,83 | N | 0,00 |
| О | 7,50 | X | 4,17 | A | 1,67 | J | 0,83 | R | 0,00 |
| M | 6,67 |
Сравнивая эти результаты с данными, показанными на рис. 1, можно заключить, что, скорее всего, буквы Р и Z шифрованного текста являются эквивалентами букв е и t открытого текста, хотя трудно сказать, какой именно букве — Р или Z — соответствует е, а какой — Z. Буквы S, U, О, М и Н, обладающие относительно высокой частотой появления в тексте, скорее всего, соответствуют буквам из множества { r, n, i, о, а, s }. Буквы с низкой частотой появления (а именно А, В, G, Y, I, J, по-видимому, соответствуют буквам множества { w,v,b,k,x,q,j,z }.
|
|

Рис. 1. Относительная частота появления букв в английском тексте
Дальше можно пойти несколькими путями. Можно, например, принять какие-то предположения о соответствиях и на их основе попытаться восстановить открытый текст, чтобы увидеть, выглядит ли такой текст похожим на что-либо осмысленное. Более систематизированный подход заключается в продолжении поиска в тексте новых характерных закономерностей. Например, может быть известно, что в рассматриваемом тексте обязательно должны присутствовать некоторые слова. Или же можно искать повторяющиеся последовательности букв шифрованного текста и пытаться определить их эквиваленты в открытом тексте.
Один из очень эффективных методов заключается в подсчете частоты использования комбинаций, состоящих из двух букв. Такие комбинации называют биграммами. Для значений относительной частоты появления в тексте биграмм тоже можно построить гистограмму, подобную показанной на рис. 1. Известно, что в английском языке самой распространенной является биграмма th. В нашем шифрованном тексте чаще всего (три раза) встречается комбинация ZW. Поэтому можно предположить, что Z соответствует t, а W — h. Тогда из ранее сформулированной гипотезы вытекает, что Р соответствует е. Заметим, что в шифрованном тексте буквосочетание ZWP имеется, и теперь мы можем представить его как the. В английском языке the является самой распространенной триграммой (т.е. комбинацией из трех букв), поэтому можно надеяться, что мы движемся в правильном направлении.
Теперь обратите внимание на комбинацию ZWSW в первой строке. Конечно, мы не можем сказать с полной уверенностью, что эти буквы принадлежат одному и тому же слову, но, если предположить, что это так, они соответствуют слову th?t. Отсюда заключаем, что букве S соответствует а.
Выяснив значение всего лишь четырех букв, мы расшифровали уже значительную часть сообщения. Продолжая анализ частоты появления букв, а также применяя метод проб и ошибок, остается проделать совсем немного работы, чтобы получить окончательный ответ. Расшифрованный исходный текст (с добавленными в него пробелами) имеет следующий вид:
it was disclosed yesterday that several informal but direct contacts have been made with political representatives of the viet cong in moscow
Моноалфавитные шифры легко раскрываются, так как они наследуют частотность употребления букв оригинального алфавита. Контрмерой в данном случае является применение для одной буквы не одного, а нескольких заменителей (называемых омофонами). Например, букве е исходного текста может соответствовать несколько разных символов шифра, (скажем, 16, 74, 35 и 21), причем каждый такой символ может использоваться либо поочередно, либо по случайному закону. Если число символов-заменителей, назначенных букве, выбрать пропорциональным частоте появления этой буквы, то подсчет частности употребления букв в шифрованном тексте становится бессмысленным. Великий математик Карл Фридрих Гаусс (Carl Friedrich Gauss) был уверен, что с использованием омофонов он изобрел шифр, который невозможно взломать. Но даже при употреблении омофонов каждому элементу открытого текста соответствует только один элемент шифрованного текста, поэтому в последнем по-прежнему должны наблюдаться характерные показатели частоты повторения комбинаций нескольких букв (например, биграмм), и в результате задача криптоанализа по-прежнему остается достаточно элементарной.
Чтобы в тексте, шифрованном с помощью методов подстановок, структура исходного текста проявлялась менее заметно, можно использовать два принципиально разных подхода. Один из них заключается в замещении не отдельных символов открытого текста, а комбинаций нескольких символов, а другой подход предполагает использование для шифрования нескольких алфавитов.
Шифр Плейфейера
Одним из наиболее известных шифров, базирующихся на методе многобуквенного шифрования, является шифр Плейфейера (Playfair), в котором биграммы открытого текста рассматриваются как самостоятельные единицы, преобразуемые в заданные биграммы шифрованного текста.
Алгоритм Плейфейера основан на использовании матрицы букв размерности 5×5, созданной на основе некоторого ключевого слова. Давайте рассмотрим пример.
| M | О | N | A | R |
| С | H | Y | В | D |
| E | F | G | I/J | К |
| L | P | O | S | T |
| U | V | W | X | Z |
В данном случае ключевым словом является monarchy (монархия). Матрица создается путем размещения букв, использованных в ключевом слове, слева направо и сверху вниз (повторяющиеся буквы отбрасываются). Затем оставшиеся буквы алфавита размещаются в естественном порядке в оставшихся строках и столбцах матрицы. Буквы I и J считаются одной и той же буквой. Открытый текст шифруется порциями по две буквы в соответствии со следующими правилами.
1. Если оказывается, что повторяющиеся буквы открытого текста образуют одну пару для шифрования, то между этими буквами вставляется специальная буква-заполнитель, например х. В частности, такое слово как balloon будет преобразовано к виду ba lx lo on.
2. Если буквы открытого текста попадают в одну и ту же строку матрицы, каждая из них заменяется буквой, следующей за ней в той же строке справа — с тем условием, что для замены последнего элемента строки матрицы служит первый элемент той же строки. Например, ar шифруется как RM.
3. Если буквы открытого текста попадают в один и тот же столбец матрицы, каждая из них заменяется буквой, стоящей в том же столбце сразу под ней, с тем условием, что для замены самого нижнего элемента столбца матрицы берется самый верхний элемент того же столбца. Например, mu шифруется как СМ.
4. Если не выполняется ни одно из приведенных выше условий, каждая буква из пары букв открытого текста заменяется буквой, находящейся на пересечении содержащей эту букву строки матрицы и столбца, в котором находится вторая буква открытого текста. Например, hs шифруется как BP, а еа — как IM (или JM, по желанию шифровальщика).
Шифр Плейфейера значительно надежнее простых моноалфавитных шифров. С одной стороны, букв всего 26, а биграмм — 26 х 26 = 676, и уже поэтому идентифицировать биграммы сложнее, чем отдельные буквы. С другой стороны, относительная частота появления отдельных букв колеблется гораздо в более широком диапазоне, чем частота появления биграмм, поэтому анализ частотности употребления биграмм тоже оказывается сложнее анализа частотности употребления букв. По этим причинам очень долго считалось, что шифр Плейфейера взломать невозможно. Он служил стандартом шифрования в Британской армии во время первой мировой войны и нередко применялся в армии США и союзных войсках даже в период второй мировой войны.
Несмотря на столь высокую репутацию в прошлом, шифр Плейфейера на самом деле вскрыть относительно легко, так как шифрованный с его помощью текст все равно сохраняет многие статистические характеристики открытого текста. Для взлома этого шифра, как правило, достаточно иметь шифрованный текст, состоящий из нескольких сотен букв.
Шифр Хилла
Еще одним интересным многобуквенным шифром является шифр, разработанный математиком Лестером Хиллом (Lester Hill) в 1929 г. Лежащий в его основе алгоритм заменяет каждые n последовательных букв открытого текста n буквами шифрованного текста. Подстановка определяется n линейными уравнениями, в которых каждому символу присваивается числовое значение (а=0, b=1,…, z = 25). Например, при n = 3, получаем следующую систему уравнений:

Эту систему уравнений можно записать в виде произведения вектора и матрицы в следующем виде:

или в виде
С=KM,
где С и M — векторы длины 3, представляющие соответственно шифрованный и открытый текст, а К — это матрица размерности 3×3, представляющая ключ шифрования. Операции выполняются по модулю 26.
Рассмотрим, например, как будет шифрован текст " рауmоrеmоnеу " при использовании ключа
 .
.
Первые три буквы открытого текста представлены вектором (15 0 24). Таким образом,
K (15 0 24) = (275 819 486) mod 26= (11 13 18) = LNS.
Продолжая вычисления, получим для данного примера шифрованный текст вида LNSHDLEWMTRW.
Для расшифровки нужно воспользоваться матрицей, обратной К. Обратной по отношению к матрице К называется такая матрица К-1, для которой выполняется равенство КК-1 = К-1К = I, где I — это единичная матрица (матрица, состоящая из нулей всюду, за исключением главной диагонали, проходящей с левого верхнего угла в правый нижний, на которой предполагаются единицы). Обратная матрица существует не для всякой матрицы, однако, когда обратная матрица имеется, для нее обязательно выполняется приведенное выше равенство. В нашем примере обратной матрицей является матрица
 .
.
Это проверяется следующими вычислениями:

Легко видеть, что в результате применения матрицы К-1 к шифрованному тексту получается открытый текст. Чтобы пояснить, как получена обратная матрица, нам придется предпринять небольшой экскурс в линейную алгебру. Определителем квадратной матрицы (n×n) называют сумму таких всевозможных произведений элементов матрицы, что в произведении каждый столбец и каждая строка представлены ровно одним элементом, причем некоторые из этих произведений, умножаются на -1. В частности, для матрицы 2×2 вида

определитель вычисляется по формуле  . Для матрицы 3×3 значение определителя подсчитывается по формуле
. Для матрицы 3×3 значение определителя подсчитывается по формуле
 .
.
Если квадратная матрица А имеет отличный от нуля определитель, то обратная матрица вычисляется как 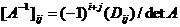 , где
, где 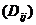 — определитель матрицы, получаемой путем удаления i -й строки и j -го столбца из матрицы А, а det(A) — определитель самой матрицы А. В нашем случае все эти вычисления проводятся по модулю 26.
— определитель матрицы, получаемой путем удаления i -й строки и j -го столбца из матрицы А, а det(A) — определитель самой матрицы А. В нашем случае все эти вычисления проводятся по модулю 26.
В общем виде систему Хилла можно записать в следующей форме:
С = ЕК(M) = КM,
Р = DК(С) = К-1С = К-1КM = M.
Как и в случае шифра Плейфейера, преимущество шифра Хилла состоит в том, что он полностью маскирует частоту вхождения отдельных букв. А для шифра Хилла чем больше размер матрицы в шифре, тем больше в шифрованном тексте скрывается информации о различиях в значениях частоты появления других комбинаций символов. Так, шифр Хилла с матрицей 3×3 скрывает частоту появления не только отдельных букв, но и двухбуквенных комбинаций.
Хотя шифр Хилла устойчив к попыткам криптоанализа в тех случаях, когда известен только шифрованный текст, этот шифр легко раскрыть при наличии известного открытого текста. Рассмотрим шифр Хилла с матрицей n×n. Предположим, что нам известны n пар отрывков открытого и соответствующего шифрованного текстов, каждый длины n. Обозначим такие пары  и
и 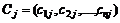 , чтобы выполнялось условие Сj = КMj для всех 1 < j < n и некоторой неизвестной ключевой матрицы К. Теперь определим две такие матрицы
, чтобы выполнялось условие Сj = КMj для всех 1 < j < n и некоторой неизвестной ключевой матрицы К. Теперь определим две такие матрицы  и
и  размера n×n, что Y = XК. Тогда, при условии что для матрицы X существует обратная матрица, К можно определить по формуле
размера n×n, что Y = XК. Тогда, при условии что для матрицы X существует обратная матрица, К можно определить по формуле  . Если же получить матрицу, обратную матрице X, невозможно, необходимо сформировать другую матрицу X с дополнительными парами соответствия открытого и шифрованного текстов, до тех пор, пока не будет найдена обратная матрица.
. Если же получить матрицу, обратную матрице X, невозможно, необходимо сформировать другую матрицу X с дополнительными парами соответствия открытого и шифрованного текстов, до тех пор, пока не будет найдена обратная матрица.
Рассмотрим пример. Предположим, что открытый текст "friday" шифрован с помощью шифра Хилла с использованием матрицы 2 × 2, в результате чего получен шифрованный текст PQCFKU. Таким образом, мы знаем, что К (5 17) = (15 16), К (8 3) = (2 5) и К (0 24) = (10 20). Используя первые две пары символов открытого и шифрованного текста, получаем
 .
.
Вычислим матрицу, обратную матрице X:
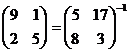 .
.
Таким образом, теперь можно получить значение ключа:
 .
.
Полученный результат можно проверить с помощью оставшихся пар открытого и шифрованного текстов.
Полиалфавитные шифры
Другая возможность усовершенствования простого моноалфавитного шифра заключается в использовании нескольких моноалфавитных подстановок, применяемых в ходе шифрования открытого текста в зависимости от определенных условий. Семейство шифров, основанных на применении таких методов шифрования, называется полиалфавитными шифрами. Подобные методы шифрования обладают следующими общими свойствами.
1. Используется набор связанных моноалфавитных подстановок.
2. Имеется некоторый ключ, по которому определяется, какое конкретное преобразование должно применяться для шифрования на данном этапе.
Самым широко известным и одновременно самым простым алгоритмом такого рода является шифр Виженера (Vigennre). Этот шифр базируется на наборе правил моноалфавитной подстановки, представленных 26 шифрами Цезаря со сдвигом от 0 до 25. Каждый из таких шифров можно обозначить ключевой буквой, являющейся буквой шифрованного текста, соответствующей букве а открытого текста. Например, шифр Цезаря, для которого смещение равно 3, обозначается ключевой буквой d.
Для облегчения понимания и применения этой схемы была предложена матрица, названная "табло Виженера" (рис. 2). Все 26 шифров располагаются по горизонтали, и каждому из шифров соответствует своя ключевая буква, представленная в крайнем столбце слева. Алфавит, соответствующий буквам открытого текста, находится в первой сверху строке таблицы. Процесс шифрования прост — необходимо по ключевой букве х и букве открытого текста у найти букву шифрованного текста, которая находится на пересечении строки х и столбца у. В данном случае такой буквой является буква V.
Чтобы зашифровать сообщение, нужен ключ, имеющий ту же длину, что и само сообщение. Обычно ключ представляет собой повторяющееся нужное число раз ключевое слово, чтобы получить строку подходящей длины. Например, если ключевым словом является deceptive, сообщение "we are discovered save yourself" шифруется следующим образом.
ключ: deceptivedeceptivedeceptive
открытый текст: wearediscoveredsaveyourself
шифрованный текст: ZICVTWQNGRZGVTWAVZlНQYGLMGJ
Расшифровать текст также просто — буква ключа определяет строку, буква шифрованного текста, находящаяся в этой строке, определяет столбец, и в этом столбце в первой строке таблицы будет находиться соответствующая буква открытого текста.

Рис. 2. Таблица Виженера
Преимущество этого шифра заключается в том, что для представления одной и той же буквы открытого текста в шифрованном тексте имеется много различных вариантов — по одному на каждую из неповторяющихся букв ключевого слова. Таким образом скрывается информация, характеризующая частотность употребления букв. Но и с помощью данного метода все же не удается полностью скрыть влияние структуры открытого текста на структуру шифрованного.
Не помешает хотя бы вкратце рассмотреть метод взлома этого шифра, так как на примере этого метода можно показать некоторые из математических принципов, лежащих в основе большинства современных методов криптоанализа.
Прежде всего предположим, что противник уверен в том, что шифрованный текст был получен либо с помощью моноалфавитной подстановки, либо с помощью шифра Виженера. Чтобы выяснить, какой именно из этих двух методов был использован, можно провести простой тест. Если использовалась моноалфавитная подстановка, статистические показатели шифрованного текста не будут отличаться от соответствующих показателей языка, на котором написан открытый текст. Так, в соответствии с рис. 1 в этом случае в шифрованном тексте один символ должен встречаться в 12,75% случаев, другой — в 9,25% и т.д. Если для анализа имеется лишь одно сообщение, точного совпадения статистических показателей можно и не получить. Но если статистика достаточно точно повторяет статистику обычного открытого текста, можно предположить, что использовалась моноалфавитная подстановка.
Если же, наоборот, все указывает на то, что был применен шифр Виженера, то, как мы увидим несколько позже, успех дальнейшего анализа текста зависит от того, удастся ли определить длину ключевого слова. Пока давайте сосредоточимся на том, как определить длину ключевого слова. Решение этой задачи основано на следующей особенности данного шифра: если начальные символы двух одинаковых последовательностей открытого текста находятся друг от друга на расстоянии, кратном длине ключа, эти последовательности будут представлены одинаковыми последовательностями и в шифрованном тексте. В рассматриваемом ниже примере имеется две последовательности " red " и начало второй из них оказывается на девять символов дальше относительно начала первой. Следовательно, в обоих случаях r будет шифровано с использованием ключевой буквы е, е — с помощью ключевой буквы р, a d — с помощью ключевой буквы t. Таким образом, в обоих случаях для шифрованного текста будет получена последовательность VTW.
Аналитик, имеющий в своем распоряжении только шифрованный текст, обнаружит повторяющуюся последовательность VTW со смещением в девять символов, и поэтому может предположить, что длина ключевого слова равна либо трем, либо девяти. Конечно, для повторившейся всего два раза последовательности VTW совпадение может оказаться и случайным, а поэтому и не соответствовать шифрованным с одинаковыми ключевыми буквами одинаковым фрагментам открытого текста, но если сообщение будет достаточно длинным, то таких повторяющихся последовательностей в нем будет немало. Определив общий множитель для смещения начала таких последовательностей, аналитик получит достаточно надежную основу для предположений о длине ключевого слова.
Дальнейший анализ базируется на другой особенности данного шифра. Если ключевое слово имеет длину N, то шифр, по сути, состоит из N моноалфавитных подстановочных шифров. Например, при использовании ключевого слова deceptive буквы, находящиеся на 1-й, 10-й, 19-й и т.д. позициях, шифруются одним и тем же моноалфавитным шифром. Это дает возможность использования известных характеристик частотных распределений букв открытого текста для взлома каждого моноалфавитного шифра по отдельности.
Периодичности в ключевой строке можно избежать, используя для ключевой строки непериодическую последовательность той же длины, что и само сообщение. Виженер предложил подход, получивший название системы с автоматическим выбором ключа, когда последовательность ключевой строки получается в результате конкатенации ключевого слова с самим открытым текстом. Для рассматриваемого примера мы получим следующее.
ключ: deceptivewearediscoveredsav
открытый текст: wearediscoveredsaveyourself
шифрованный текст: ZICVTWQNGKZEIIGASXSTSLVVWLA
Однако и эта схема оказывается уязвимой. Поскольку и в ключевой строке, и в открытом тексте значения частоты распределения букв будут одинаковы, статистические методы можно применить и в данном случае. Например, буква е, шифрованная с помощью ключа е, согласно рис. 1, должна встречаться с частотой (1275)2 = 0,0163, тогда как d, шифрованная с помощью t, может встретиться с частотой, примерно в два раза меньшей. Именно такие закономерности позволяют добиться успеха при анализе шифрованного текста.
Лучшей защитой от подобных методов криптоанализа является выбор ключевого слова, по длине равного длине открытого текста, но отличающегося от открытого текста по статистическим показателям.
Контрольные вопросы
1. Дайте определение криптографии и криптоанализа. В чем состоит их различие?
2. Перечислите разделы криптологии.
3. Что такое алфавит.
4. Дайте определение понятиям закрытый и открытый текст.
5. Что такое ключ?
6. В чем состоит различие симметричных и асимметричных систем шифрования?
7. Что такое электронно-цифровая подпись?
8. Что такое криптостойкость, и какие ее основные показатели?
9. Какие общие требоания выдвигаются к криптосистемам?
10. В чем суть шифрования с использованием логической операции XOR?
11. Какие рекомендации для повышение надежности шифрования методом XOR вы можете дать?
12. В чем заключается принцип шифрования с использованием моноалфавитной подстановки?
13. Как раскрыть шифр, полученный с помоью моноалфавитной подстановки?
14. В чем заключается суть частотного анализа шифротекста?
15. Что такое омофоны? Для чего они используются?
16. Опишите принцип шифрования с использованием шифра Плейфейра.
17. Охарактеризуйте криптостойкость шифра Плейфейра.
18. Каков принцип шифрования с использованием метода Хилла.
19. Что такое полиалфавитные шифры?
20. В чем суть шифрования с применением таблицы Виженера?
21. Каким образом осуществляется взлом шифротекста, сформированного с помощью таблицы Виженера?