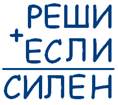
Так как наибольшая цифра в числе «СИЛЕН» равна 5, а С = 1, то остальные 4 цифры в данном числе будут 2, 3, 4, 5.
Так как Н < 6, то И = 2. А значит, Н = 4. Так как Л > Е (в самом деле так как Е + 1 = Л, то Л > Е, ведь Л и Е меньше 5 по условию), то Л = 5, Е = 3.
А тогда уже легко находим остальные цифры: Ш = 8, Р = 9.
В итоге получается: 9382 + 3152 = 12534
Ответ: 9382 + 3152 = 12534
VIII Задачи, решаемые с конца
Я задумал число, умножил его на 7, прибавил 15 и получил 50. Какое число я задумал?
50 – 15 = 35 – число, до прибавления 15.
35: 7 = 5 – искомое число.
Ответ. 5 – задуманное число.
Маша принесла своим друзьям медведям торт. Известно, что старший медведь съедает торт за 2 дня, средний медведь – за 3 дня, младший медведь – за 6 дней. За сколько дней три медведя вместе съедят торт?
Так как старший медведь съедает торт за 2 дня, то за 1 день он съедает 12 торта.
Так как средний медведь съедает торт за 3 дня, то за 1 день он съедает 13 торта.
Так как младший медведь съедает торт за 6 дней, то за 1 день она съедает 16 торта.
Вместе все три медведя за 1 день съедят 12+13+16=1, то есть один торт.
Ответ. За 1 день.
Домашнее задание
№1. Атос, Портос, Арамис и Д’Артаньян – четыре талантливых молодых мушкетёра. Один из них лучше всех сражается на шпагах, другой не имеет равных в рукопашном бою, третий лучше всех танцует на балах, четвертый без промаха стреляет с пистолетов. О них известно следующее:
• Атос и Арамис наблюдали на балу за их другом – прекрасным танцором.
• Портос и лучший стрелок вчера с восхищением следили за боем рукопашника.
• Стрелок хочет пригласить в гости Атоса.
• Портос был очень большой комплекции, поэтому танцы были не его стихией.
Кто чем занимается?
№2. Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
№3. Летом Винни-Пух сделал запас меда на зиму и решил разделить его пополам, чтобы съесть половину до Нового Года, а другую половину - после Нового года. Весь мед находится в ведре, которое вмещает 6 литров, у него есть 2 пустые банки - 5-литровая и 1-литровая. Может ли он разделить мед так, как задумал?
№4. Среди 101 одинаковых по виду монет одна фальшивая, отличающаяся по весу. Как с помощью чашечных весов без гирь за два взвешивания определить, легче или тяжелее фальшивая монета? Hаходить фальшивую монету не требуется.
 №5.
№5.
№6. Крестьянин пришел к царю и попросил: «Царь, позволь мне взять одно яблоко из твоего сада». Царь ему разрешил. Пошел крестьянин к саду и видит: весь сад огорожен тройным забором. Каждый забор имеет только одни ворота, и около каждых ворот стоит страж. Подошел крестьянин к первому стражу и сказал: «Царь разрешил мне взять одно яблоко из сада». «Возьми, но при выходе должен будешь отдать мне половину яблок, что возьмешь, и еще одно», - поставил условие страж. Это же повторили ему второй и третий, которые охраняли другие ворота. Сколько яблок должен взять крестьянин, чтобы после того, как отдаст положенные части трем стражам, у него осталось одно яблоко?
№7. Незнайка услышал разговор Сиропчика, Пилюлькина, Торопыжки и Знайки. Известно, что каждый из них либо всегда лжет, либо всегда говорит правду.
1) Сиропчик обвинил Пилюлькина в том, что он – лгун.
2) Знайка сказал Сиропчику: «Сам ты лгун!».
3) Торопыжка заметил: «Оба они лгуны».
4) Знайка спросил у Звезды «А я?».
5) На что Торопыжка ответил «И ты тоже лгун!»
«Кто же из них говорит правду?» - удивился Незнайка. Помогите ему.