Теорема кантора.
Т 15.1
Функция 
непрерывна на отрезке [a, b] 
равномерно непрерывна на нём.
Доказательство:
Вследствие непрерывности функции f в 
по заданному 
 |
 |
 |
Заметим, что, еслиточка х’’ ещё одна очка 
.(15.4)
Наряду с 
(x) рассмотрим 
.Семейство таких интервалов покрывает отрезок [a, b] 
|
|
также покрывающих отрезок [a, b].
 |
Поэтому на основании 15.4 
.
Теорема доказана.
Теорема Вейерштрасса о непрерывности функций.
Следующая теорема верна в приложениях
Т 16.1
непрерывна на отрезке [a, b], имеет на этом отрезке минимальное и максимальное значение. 
Доказательство:
Докажем, что функция fограничена на отрезке [a, b]. По теореме Кантора функция непрерывно равномерна на [a, b]. По числу 
найдется число 
, такое, что, для любых точек 
. 
Разделим отрезок[a, b] точками 
на конечное число 
отрезков, каждый из которых имеет длину 
.
 |
 |
Выберем произвольную точку 
пусть она попала в выбранной отрезок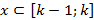 
.
Далее имеем:
Отсюда получается оценка: 
с правой частью независимой от x 
. Тем самым ограниченность функции на отрезке 
доказана.
Пусть теперь 
.
Тогда 
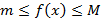, при чем m и M – конечны.(16.1)
Покажем, что значение mдостигается функцией f в некоторой точке отрезка [a, b]. Предполагая от противного, будем иметь на отрезке [a, b] строгое неравенство:
Но тогда получается, что на отрезке [a, b] непрерывна функция 
, но тогда на основании первой части доказательства функция ограничена на отрезке [a, b] в частности существует:
но тогда получается неравенство 
.
Но это противоречит определению числа m. Противоречие означает, что в некоторой точке 
для которой выполнено равенство: 
.
В силу неравенства 16.1 m - минимальное значение на отрезке [a, b]. Аналогично заказывается что в некоторой точке 
Но тогда в силу 16.1M -максимальное значение.
Теорема доказана.
Замечание: как показывает пример функции:
Для существования экстремальных(максимального, минимального) значение, определенных на отрезке, условия непрерывности необходимо.
Но даже непрерывности функции оказывается недостаточно, если вместо отрезка взять интервал или полуинтервал. Это видно на примере при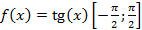 
.
Теорема Вейерштрасса о монотоннойфункции.
Вещественная функция 
называется возрастающей/убывающей на множестве Х, если выполняется следующее условие:
Если соответствующее неравенство между f(x), f(x’) – строгое неравенство, то говорят о непрерывном возрастании или убывании функции f(x)
Т. 12.2
Пусть 
монотонна на множестве X, имеет предельную точку A, достижимую слева (справа), тогда функция f в точке a имеет предел слева (справа) если функция f ограничена на множестве 
(ограниченное на 
) при 
, то этот предел конечный, в противном случае – бесконечный.
Доказательство:
Для определения будем считать функцию fвозрастающей на множестве X, а точку а – достижимой слева. Прочие случаи рассматриваются аналогично.
Сначала рассмотрим ситуацию функции fограниченной на множестве 
при 
. В этом случае 
на множестве 
функция f ограничена 
величина 
Докажем, что 
предел слева. Пусть задана 
, по свойству верхней границы слева. Тогда 
такая, что 
.
Рассмотрим проколотую окрестность 
Ввидувозрастания функции fдля любого xиз 
получается: 
.
Следовательно, при 
Но последнее и означает, что Aслужит пределом слева. Рассмотрим случай, когда функция не ограничена: 
Рассмотрим проколотую окрестность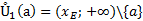 
, тогда в силу возрастания функции fдля 
 | |||
 | |||
f(x) лежит в окрестности (E; +∞).
Это означает, что f(x) при 
на множестве имеет предел +∞в этом случае 
Теорема доказана.
Замечание: из доказательства нетрудно усмотреть в каком случае соответственный односторонние пределы оказываются равными 
Если справа функция возрастает, то предел равен 
