К структуре ЦФ, приближенно соответствующего известной аналоговой цепи, можно прийти, осуществив дискретизацию дифференциального уравнения, описывающего аналоговый прототип. Как пример использования этого метода рассмотрим синтез ЦФ, отвечающего колебательной динамической системе 2-го порядка, для которой связь между выходным колебанием y(t) и входным колебанием x(t) устанавливается дифференциальным уравнением
(4.2)
Предположим, что шаг дискретизации равен Dt и рассмотрим совокупности дискретных отсчетов {у1} и {х1}. Если в формуле заменить производные их конечно-разностными выражениями, то дифференциальное уравнение превратиться в разностное уравнение
. (4.3)
Перегруппировав слагаемые, получим:
(4.4)
Разностное уравнение задает алгоритм рекурсивного фильтра 2-го порядка, который моделирует аналоговую колебательную систему и называется цифровым резонатором. При соответствующем выборе коэффициентов цифровой резонатор может выполнять роль частотно-избирательного фильтра, подобного колебательному контуру.
Метод инвариантных частотных характеристик.
Принципиально невозможно создать ЦФ, частотная характеристика которого в точности повторяла бы частотную характеристику некоторой аналоговой цепи. Причина состоит в том, что, как известно, частотный коэффициент передачи ЦФ является периодической функцией частоты с периодом, определяемым шагом дискретизации.
Говоря о подобии (инвариантности) частотных характеристик аналогового и цифрового фильтров, можно требовать лишь то, чтобы весь бесконечный интервал частот ωа, относящихся к аналоговой системе, был преобразован в отрезок частот ωц цифрового фильтра, удовлетворяющих неравенству 
при сохранении общего вида АЧХ.
Пусть Kа(р) - передаточная функция аналогового фильтра, задаваемого дробно-рациональным выражением по степеням p. Если воспользоваться связью между переменными z и p,то можно записать:
. (4.5)
С помощью этого закона связи между p и z нельзя получить физически реализуемую системную функцию фильтра, так как подстановка в выражение Kа(р) даст системную функцию, не выражающуюся в виде частного двух многочленов. Поэтому для синтезов фильтров нижних частот получила распространение связь вида
, (4.6)
которая также переводит точки единичной окружности, лежащей в плоскости z, в точки мнимой оси на плоскости p. Тогда
, (4.7)
откуда вытекает соотношение между частотными переменными w аналоговой и цифровой систем:
. (4.8)
Если частота дискретизации достаточно велика (wцT<<1), то, как легко видно из формулы (4.7), wа»wц. Таким образом, на низких частотах характеристики аналогового и цифрового фильтров практически совпадают. В общем случае нужно принимать во внимание трансформацию масштаба по оси частот цифрового фильтра.
Практически процедура синтеза ЦФ состоит в том, что в функции Kа(р) аналоговой цепи выполняется замена переменной по формуле (4.5). Полученная при этом системная функция ЦФ оказывается дробно-рациональной и поэтому позволяет непосредственно записать алгоритм цифровой фильтрации.
Порядок выполнения лабораторной работы.
1. Синтезировать методом инвариантных частотных характеристик низкочастотный цифровой фильтр с частотной характеристикой, подобной характеристике аналогового ФНЧ 2-го порядка типа Баттерворта. Частота среза для цифрового фильтра wсц=1600 с-1, частота дискретизации wд=20000 с-1.
2. Передаточная функция аналогового ФНЧ 2-го порядка типа Баттерворта имеет вид
,
где wса - частота среза аналогового прототипа, определяется по wсц через формулу связи аналоговых и цифровых частот.
3. Определить K(jw) цифрового фильтра для w от 0 до 50000 с-1.
4. Вычислить и вывести на экран АЧХ цифрового и аналогового фильтров
5. При выводе графика использовать логарифмический масштаб по оси частот.
6. Синтезировать цифровой фильтр высокой частоты, аналоговый прототип которого имеет передаточную функцию
.
7. Вычислить и вывести на экран графики АЧХ цифрового и аналогового фильтров. Сравнить с АЧХ низкочастотного фильтра.
8. Синтезировать полосовой и режекторный цифровые фильтры, аналоговые прототипы которых имеют передаточные функции
, 
,
где частота настройки для цифрового фильтра wсц=2000 с-1, добротность фильтра Q=50, частота дискретизации wд =20000 с-1.
9. Вычислить и вывести на экран графики АЧХ цифрового и аналогового фильтров. Проверить, как изменяются избирательные свойства фильтров при увеличении или уменьшении значения добротности Q.
10. Методом инвариантных частотных характеристик синтезировать три цифровых низкочастотных фильтра Чебышева второго порядка для трех различных уровней пульсаций в полосе пропускания (0,5 dB; 1,0 dB; 3 dB). Частота среза wсц=2000 с-1, частота дискретизации wд=20000 с-1.
Передаточные функции аналоговых прототипов имеют вид
,
где значения N, a, b зависят от уровня пульсаций в полосе пропускания.
Для пульсаций 0,5 dВ - N =1,431, a = 1,426, b =1,516.
Для пульсаций 1,0 dВ - N =0,983, a = 1,098, b =1,103.
Для пульсаций 3 dВ - N =0,500, a = 0,644, b =0,707.
12. Вычислить и вывести на экран графики АЧХ цифрового и аналогового фильтров.
13. Преобразовать фильтр низких частот в фильтр высоких частот. Для этого в выражении для K(p) произвести замену
.
14. Вычислить и вывести на экран графики АЧХ цифрового и аналогового высокочастотных фильтров.
15. Преобразовать фильтр низких частот в полосовой фильтр. Для этого в выражении для K(p) произвести замену
,
где wса - центральная частота полосы пропускания аналогового прототипа, для цифрового фильтра wсц=3000 с- 1,
П - ширина полосы пропускания фильтра, для расчета взять значение П=100 и 500.
Примечание: преобразование фильтра нижних частот в полосовой фильтр удваивает его порядок.
6. Вычислить и вывести на экран графики АЧХ цифрового и аналогового полосовых фильтров.
Контрольные вопросы.
1. В чем суть метода дискретизации дифференциального уравнения?
2. В чем суть метода инвариантных импульсных характеристик?
3. Почему для нахождения системной функции H(z) по выражению для K(p) используют соотношение (4.4), а не (4.3)?
4. Как связаны частоты аналогового прототипа и синтезируемого цифрового фильтра?
5. Как классифицируются фильтры?
6. Какие фильтры называются фильтрами Баттерворта?
7. Какие фильтры называются фильтрами Чебышева?
8. Какие типы фильтров Вы еще знаете, и в чем отличие их частотных коэффициентов передачи от фильтров Баттерворта и Чебышева?
9. К рекурсивным или трансверсальным относятся цифровые фильтры, рассмотренные в лабораторной работе?
10. Как перейти от НЧ фильтра к ВЧ или полосовому фильтрам?
ЛИТЕРАТУРА
1.Гоноровский И.С. Радиотехнические цепи и сигналы.
2.Конспект лекций по курсу "Теоретические основы информационной техники".
3.Гутников В.С. Фильтрация измерительных сигналов. - Л.: Энергоатомиздат,1990.
ЛАБОРАТОРНАЯ РАБОТА №5
ЛИНЕЙНО-ЧАСТОТНО МОДУЛИРОВАННЫЙ (ЛЧМ) СИГНАЛ
Цель работы
Изучить сигналы с угловой модуляцией на примере ЛЧМ-сигнала.
Краткие теоретические сведения
ЛЧМ сигнал является сигналом с угловой модуляцией 
.
Пусть в течение времени T сигнал S(t) меняет мгновенное значение своей частоты линейно, и нарастает она от 
до 
, где f0 – центральная частота сигнала, а fд – девиация частоты. Примем за начало отсчёта t = 0 момент времени, соответствующий середине изменения частоты и запишем выражение для закона частоты и фазы в диапазоне времени t, равном
Тогда: 
Найдём выражение для y(t):
,
Примем 
.
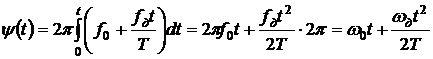(5.1)
Сигнал S(t) представляет собой ЛЧМ - импульс и показан на рис. 5.1.
, 
.
Используя понятие аналитического сигнала, ЛЧМ-сигнал можно записать в виде:
В нашем случае частота модулируется по линейно-нарастающему закону в течение интервала времени T и в первом приближении за ширину спектра модулирующего сообщения можно принять величину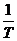 
. А полный диапазон изменения частоты сигнала равен fд (fд >> ).
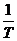Следовательно, индекс угловой модуляции m равен
В этом случае ширина спектра ЛЧМ-сигнала равна 
Рис. 5.1. Линейно частотно-модулированный сигнал
Задача сводится к определению корреляционной функции комплексной огибающей ЛЧМ сигнала:
- нормированная корелляционная функция.
.
При вычислении 
учтём, что для любых 
из интервала 
произведение 
отлично от нуля лишь при t, находящихся в пределах 
С учетом этого
После интегрирования получим
Так как 
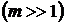, то 
.
На рис. 2 показан вид корреляционной функции.
Рис. 5.2. Корреляционная функция комплексной огибающей.
Замечательное свойство ЛЧМ-сигналов, определяющее их практическую значимость, состоит в следующем. Предположим, что имеется некоторое физическое устройство, осуществляющее задержку сигналов, подаваемых на его вход. Если время задержки зависит от частоты сигнала, причем с ростом частоты это время уменьшается, то при определенных условиях, подавая на вход такого устройства ЛЧМ -импульс большой длительности, можно добиться существенного «сжатия» его во времени. Этот эффект обусловлен тем, что на выходе устройства задержки одновременно будут появляться составляющие как более низкочастотные, относящиеся к началу импульса, так и более высоко-частотные, наблюдаемые в его конце.
Длительность основного лепестка корреляционной функции много меньше длительности Т ЛЧМ сигнала, т.е. если ЛЧМ сигнал подавать на устройство, выходной сигнал которого является корреляционной функцией входного сигнала, то можно говорить об эффекте сжатия ЛЧМ импульса (рис. 5.3).
Для ЛЧМ импульса длительностью 10-100 мкс. и девиации частоты до десятков МГц, согласованные фильтры строят с использованием дисперсионных линий задержек на поверхностных акустических волнах.
Рис. 5.3.Пример эффекта сжатия ЛЧМ сигнала
При рассмотрении корреляционной функции за длительность tk была принята ширина основного лепестка корреляционной функции. Однако выбросы корреляционной функции за пределами основного лепестка достигают значительного уровня: 2-ой лепесток всего лишь в 4,7 (13дБ) ниже основного. Поэтому боковые лепестки могут повысить риск при измерении времени запаздывания ЛЧМ сигнала, и затруднить разрешение 2-х ЛЧМ импульсов с разносом времени, близким к tk.
Из анализа корреляционной функции мы видим, что спектральная плотность ЛЧМ сигнала близка к прямоугольной форме (рис.5. 4).
Рис.5. 4. Вид энергетического спектра для разных значений индекса угловой модуляции m (2…5, 20, 100)
Порядок выполнения работы
1. По заданной преподавателем 
, 
и m в соответствие с теоремой Котельникова определить шаг дискретизации, длительность ЛЧМ- сигнала и число отсчетов N из сигнала.
2. Определить выборки из ЛЧМ – сигнала.
3. С помощью средств MathCada вычислить дискретное преобразование Фурье по выборкам сигнала.
4. Рассчитать корреляционную функцию комплексной огибающей заданного сигнала.
5. Повторить пункты 2 – 5 для значений m = 10, 25, 50.
Содержание отчета
Отчет должен содержать исходные данные, порядок расчетов, графики спектров и корреляционных функций, а также график ЛЧМ - сигнала.
Контрольные вопросы
1. Какими соотношениями связаны мгновенная частота и фаза сигнала?
2. Что называется индексом угловой модуляции?
3. Чему равна ширина спектра сигнала с угловой модуляцией при m <<1 и при m >>1.
4. В чем заключается эффект сжатия ЛЧМ –сигнала?
5. Какой сигнал называется аналитическим?
6. Назовите свойства аналитического сигнала.
7. Как определяется фаза аналитического сигнала?
Литература
1. Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник для вузов.- М.: Радио и связь,1986.-512с.
2. Ширман Я. Д. Разрешение и сжатие сигналов. – М.: Сов. радио, 1974. -360 с.