Поиск цепочек символов
Текстовые редакторы, трансляторы, антивирусные программы
Алфавит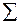 
– мн-во знаков (символов), из к-рых строятся цепочки. 
– мощность алфавита.
Цепочки (строки) образуются с помощью конкатенации:
=> 
– мн-во цепочек длины 2.
– мн-во цепочек 
длины 
: 
, 
.
единственная пустая цепочка 
.
– итерация алфавита.
Основные понятия и обозначения
Цепочка (строка, текст) длины 
:
– конкатенация символов алфавита (
, 
). Для простоты изложения будем индексировать символы в строке от 1 (в том числе, и в программах).
Префикс (длины 
) строки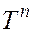 
:
, 
, 
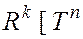– начальных символов 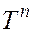(можно обозначить просто 
).
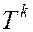Суффикс (длины 
) строки :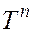
, 
, 
– конечных символов .
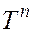Задача поиска подстроки
Даны строка (текст) 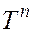и подстрока (образец) 
, 
, 
.
Найти все случаи вхождения в 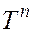, т.е. все значения 
, для которых выполняется:
.
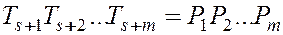Величины 
, определяющие, какие символы строки 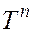будут сравниваться с символами подстроки , будем называть сдвигами ( относит-но 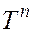). Очевидно, что 
. Сдвиги, соответствующие вхождениям в 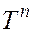, называются допустимыми.
Простейший алгоритм:
последовательно проверить условие 
для всех сдвигов .
for (s = 0; s <= n-m; s++) {
for (i=s+1, j=1; j<=m && T[i]==P[j]; j++,i++);
if (j > m) найдено_вхождение;
}
Основной недостаток данного алгоритма – постоянный сдвиг подстроки на 1, независимо от результатов сравнения символов. Трудоемкость наиболее высока при малой мощности алфавита (много совпадений символов и 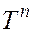) и в наихудшем составляет 
.
Алгоритм Бойера-Мура (вариант с таблицей сдвигов)
Основная идея: сравнивать пары символов 
и 
от конца подстроки и по результатам сравнения исключать заведомо недопустимые сдвиги.
Пример (красн. стрелками отмечены несовпадения символов)
 |
Символы строки и подстроки сравниваются от конца подстроки. Независимо от того, является ли текущий сдвиг допустимым (найдено вхождение) или нет, величину следующего сдвига определяет символ 
(который сравнивался с последним символом подстроки 
).
Для подстроки необходимо построить таблицу сдвигов длины , в которой каждому символу алфавита соответствует величина приращения текущего сдвига (на сколько позиций от текущего положения нужно сдвинуть ). -й элемент данной таблицы соответствует символу 
и равен:
, если не входит в 
(первые 
символов );
, где 
- позиция самого правого вхождения 
в , в противном случае.
Построение таблицы сдвигов 
для подстроки длины и стандартного набора из 256 символов:
for (k = 0; k < 256; k++) D[k] = m;
for (k = 1; k < m; k++) D[ord(P[k])] = m – k;
Поиск подстроки в тексте длины :
for (s = 0; s <= n-m;) {
for (i=s+m, j=m; j>0 && T[i]==P[j]; j--, i--);
if (j == 0) найдено_вхождение;
s += D[ord(T[s+m])];
}
Трудоемкость в наилучшем: 
.
Трудоемкость в наихудшем: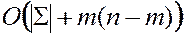 
.
Алгоритм наиболее пригоден для большого входного алфавита и нечастого появления подстроки в тексте.
Поиск подстроки с помощью конечного автомата
КА – это пятерка (
), где
- конечное множество состояний,
- начальное состояние,
- множество допускающих состояний,
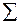- входной алфавит,
- функция переходов (
).
Для строки-образца определим суффикс-функцию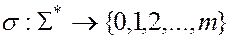 
: для произвольной строки 
значение 
равно длине максимального суффикса 
, являющегося префиксом 
, т.е.
.
Примеры значений суффикс-функции для 
:
, 
, 
, 
.
Определим мн-во состояний КА для распознавания 
:
, 
, 
.
КА просматривает символы входной строки 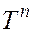слева направо. Если после проверки символа 
текущее состояние равно 
, то это означает, что ровно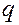 
последних проверенных символов 
совпадают с начальными символами :
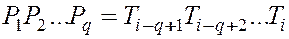, т.е. 
.
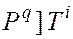По определению суффикс-функции из этого следует:
.
КА находится в состоянии 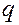, проверяет очередной символ 
и переходит в новое состояние 
.
Используем это условие для задания функции переходов КА:
, 
.
Примеры переходов для (текущее состояние 
, анализируемые символы выделены красным):
 |
 |
 |
Таблица переходов и КА для 
и 
(переходы в состояние 0 не указаны):
| a | b |  c
| |
Построение таблицы переходов 
для произвольной подстроки 
и алфавита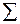 
:
for (q = 0; q <= m; q++)
foreach a 
{
for (k = min(m, q+1); k > 0; k--) {
// 
является суффиксом 
?
if (P[k]!= a) continue;
for (i = k-1, j = q; i > 0; j--, i--)
if (P[i]!= P[j]) break;
if (i == 0) break; // - суффикс 
} D[q][a] = k;
}
Трудоемкость данного алгоритма составляет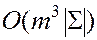 
,
размер таблицы – 
элементов.
Поиск всех вхождений подстроки в строку 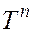после построения таблицы переходов :
for (q = 0, i = 1; i <= n; i++) {
q = D[q][T[i]];
if (q == m) найдено_вхождение(i–m);
}
Трудоемкость поиска подстроки составляет 
.
Наиболее выгодно использовать КА для распознавания подстрок, если входной алфавит содержит мало символов и длина подстроки-образца 
невелика.