Алгоритм КМП похож на алг-м распознавания с помощью КА, но позволяет избавиться от главного недостатка последнего – высокой трудоемкости построения таблицы переходов и затрат памяти на ее сохранение.
В алгоритме КМП строится не КА, а похожая на него машина распознавания, которая может делать несколько последовательных переходов из текущего состояния при анализе очередного символа текста.
Рассмотрим пример распознавания подстроки  (выделены совпадающие символы текста и
(выделены совпадающие символы текста и  , текущее состояние
, текущее состояние  , анализируемый символ
, анализируемый символ  – красный):
– красный):
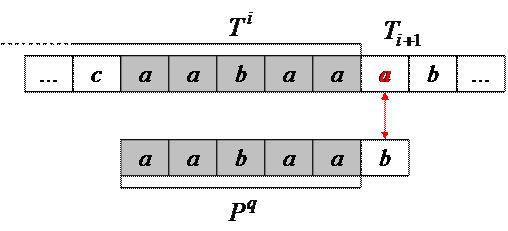
 , но
, но  , поэтому машина не может перейти в
, поэтому машина не может перейти в  , а должна перейти в новое состояние
, а должна перейти в новое состояние 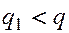 (т.е.
(т.е.  сдвинется вправо относительно
сдвинется вправо относительно  ). Используя уже проверенную
). Используя уже проверенную  , перейдем в наибольшее возможное состояние
, перейдем в наибольшее возможное состояние  , для к-го
, для к-го  , и сравним
, и сравним  и
и  :
:


 , повторяем попытку для макс-ного
, повторяем попытку для макс-ного  ,
,  :
:
 : переходим в сост-е
: переходим в сост-е  , символ
, символ  проверен.
проверен.
Отметим, что текущий анализируемый символ  никак не влияет на выбор следующего состояния машины распознавания: в состоянии
никак не влияет на выбор следующего состояния машины распознавания: в состоянии  (для к-рого
(для к-рого  ) выбирается максимальное состояние
) выбирается максимальное состояние  , для к-рого
, для к-рого  .
.
При этом  , т.е.
, т.е.  является максимальным по длине префиксом
является максимальным по длине префиксом  , который совпадает с суффиксом
, который совпадает с суффиксом  . Отсюда следует, что очередное состояние определяется только подстрокой
. Отсюда следует, что очередное состояние определяется только подстрокой  и никак не зависит от проверяемого текста
и никак не зависит от проверяемого текста  .
.
Для поиска нужного состояния при распознавании подстроки-образца  заранее вычисляется целочисленная префикс-функция (функция отказов):
заранее вычисляется целочисленная префикс-функция (функция отказов):
 ,
,  .
.
Таблица значений  для подстроки
для подстроки  :
:

| ||||||

|
Машина распознавания подстроки  :
:
 |
Последовательность состояний при анализе строк:
aabaaa … 1-2-3-4-5-2-1-2...
aabaab … 1-2-3-4-5-6…
aabaac … 1-2-3-4-5-2-1-0…
При анализе очередного символа  возможен возврат через несколько состояний.
возможен возврат через несколько состояний.
Если текущее состояние  , то можно сделать
, то можно сделать  переходов в предыдущие состояния.
переходов в предыдущие состояния.
Но если машина распознавания находится в состоянии  , должно выполняться условие
, должно выполняться условие 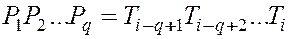 .
.
=>
При анализе символов  было сделано ровно
было сделано ровно  переходов в последующие состояния (по одному переходу на каждый символ, без переходов в предыдущие).
переходов в последующие состояния (по одному переходу на каждый символ, без переходов в предыдущие).
=>
На каждый проверяемый символ текста приходится в среднем  переходов.
переходов.
Вычисление префикс-функции  для подстроки
для подстроки  :
:
F[1] = 0;
for (q = 2; q <= m; q++) {
k = F[q–1];
while (k > 0 && P[q]!= P[k+1]) k = F[k];
F[q] = (P[q] == P[k+1])? k+1: 0;
}
В цикле while можно сделать максимум  шаг, но это возможно, если до этого был выполнен
шаг, но это возможно, если до этого был выполнен  шаг цикла for, на которых цикл while вообще не выполнялся.
шаг цикла for, на которых цикл while вообще не выполнялся.
=>
Общая трудоемкость данного алгоритма составляет  .
.
Поиск всех вхождений подстроки  в строку
в строку 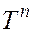 после вычисления префикс-функции
после вычисления префикс-функции  :
:
for (q = 0, i = 1; i <= n; i++) {
while (q > 0 && P[q+1]!= T[i]) q = F[q];
if (P[q+1] == T[i]) q++;
if (q == m) {
найдено_вхождение(i–m); q = F[q];
}
}
Рассуждая по аналогии с алгоритмом вычисления  , можно сделать вывод, что трудоемкость данного алгоритма
, можно сделать вывод, что трудоемкость данного алгоритма  .
.
=>
Общая трудоемкость алгоритма КМП составляет  и не зависит от количества символов в алфавите.
и не зависит от количества символов в алфавите.
Вариант алгоритма Бойера-Мура с вычислением функций стоп-символа и безопасного суффикса (Кормен).
Алгоритм Рабина-Карпа
При поиске подстроки  в строке
в строке 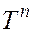 необходимо найти все допустимые сдвиги, т.е. такие значения
необходимо найти все допустимые сдвиги, т.е. такие значения  ,
,  , для которых
, для которых  .
.
Основная идея алгоритма:
- преобразовать подстроку  и сравниваемую с ней часть текста
и сравниваемую с ней часть текста  в целые числа, заданные
в целые числа, заданные  цифрами в системе счисления с основанием
цифрами в системе счисления с основанием  (обозначим эти числа, соответственно,
(обозначим эти числа, соответственно,  и
и  );
);
- сравнивать не  и
и  , а
, а  и
и  (одно сравнение чисел вместо
(одно сравнение чисел вместо  сравнений символов);
сравнений символов);
- обеспечить быстрое вычисление числа  , соответствущего сдвигу
, соответствущего сдвигу  , преобразованием значения
, преобразованием значения  .
.
Пусть  . Тогда:
. Тогда:


Сдвиг  является допустимым, если
является допустимым, если  .
.
Для вычисления  не требуется знание строки
не требуется знание строки  . Используя схему Горнера, можно получить
. Используя схему Горнера, можно получить  за время
за время  :
:

Также за  можно вычислить
можно вычислить  :
:

Значения  и
и  связаны рекуррентным соотношением:
связаны рекуррентным соотношением:

Если заранее получить константу  (за время
(за время  ), то
), то  будет вычисляться по известному
будет вычисляться по известному  за
за  ЭШ, а проверку всего текста
ЭШ, а проверку всего текста 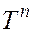 можно провести за
можно провести за  .
.
К сожалению, числа  и
и  могут быть очень большими. Если
могут быть очень большими. Если  , то уже при
, то уже при  мы выйдем за пределы представления 4-байтовых целых чисел. Поэтому отдельные арифметические операции, на основании которых получены оценки трудоемкости, нельзя считать элементарными шагами.
мы выйдем за пределы представления 4-байтовых целых чисел. Поэтому отдельные арифметические операции, на основании которых получены оценки трудоемкости, нельзя считать элементарными шагами.
Для преодоления этой трудности нужно перейти к модульной арифметике: вместо сверхдлинных целых чисел использовать их остатки от деления по некоторому модулю  .
.
Если задано некоторое целое  , то любое произвольное целое
, то любое произвольное целое 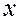 можно единственным образом представить в виде:
можно единственным образом представить в виде:
 , где
, где 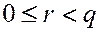 (
( - частное,
- частное,  - остаток).
- остаток).
Для любых целых 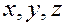 выполняется равенство:
выполняется равенство:
 ,
,
т.е. операцию деления по модулю можно вносить в скобки и применять к отдельным значениям.
Чтобы исключить переполнение для целых в алгоритме Рабина-Карпа необходимо выбрать такое  (простое), чтобы значение
(простое), чтобы значение  помещалось в машинное слово, и при расчете
помещалось в машинное слово, и при расчете  ,
,  ,
, 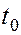 и
и 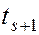 постоянно вычислять остатки по
постоянно вычислять остатки по  :
:
вместо  использовать
использовать  ; при вычислении
; при вычислении  брать остаток после каждого умножения текущего числа на
брать остаток после каждого умножения текущего числа на 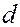 ,
,
 ,
,
 ,
,
 .
.
Приведенные выше оценки трудоемкостей сохранятся, но теперь все вычисления проводятся с короткими числами, и каждая арифметическая операция будет одним ЭШ.
Пример вычисления  для строки из десятичных цифр (
для строки из десятичных цифр ( ,
,  , Кормен и др.):
, Кормен и др.):
 |
14152 = (31415 - 3∙10000) ∙10 + 2 – для длинных целых.
14152 mod 13 =
= ((31415 mod 13 – (3∙10000) mod 13) ∙10 + 2) mod 13 =
= ((7 – 9) ∙10 + 2) mod 13 = 8 – для остатков.
Правильное вычисление r = a mod q (при q > 0):
r = a % q;
if (r < 0) r += q;
Если  , то и
, то и  . Но из
. Но из  еще не следует
еще не следует  . Поэтому при совпадении остатков необходимо проверить, найдено ли действительно вхождение подстроки (т.е. выполняется ли
. Поэтому при совпадении остатков необходимо проверить, найдено ли действительно вхождение подстроки (т.е. выполняется ли 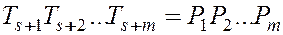 ) или произошло холостое срабатывание.
) или произошло холостое срабатывание.
В наихудшем случае (например, если  и
и  являются последовательностями из одного символа алфавита) будет постоянно выполняться
являются последовательностями из одного символа алфавита) будет постоянно выполняться  и последующее посимвольное сравнение. Поэтому трудоемкость в наихудшем составляет
и последующее посимвольное сравнение. Поэтому трудоемкость в наихудшем составляет  , как в простейшем алгоритме.
, как в простейшем алгоритме.
Но в большинстве практических приложений совпадений остатков и холостых срабатываний должно быть немного, и трудоемкость алгоритма Рабина-Карпа составит  .
.
Поиск всех вхождений  в
в  (
( ):
):
p = P[1]; t = T[1]; h = 1;
for (i = 2; i <= m; i++) {
h = mod(h*d, q);
p = mod(p*d + P[i], q);
t = mod(t*d + T[i], q);
}
for (s = 0; s <= n-m; s++) {
if (p == t) {
for (i = 1; i <= m && P[i] == T[s+i]; i++);
if (i > m) найдено_вхождение(s);
}
if (s < n-m)
t = mod(mod(t–T[s+1]*h, q)*d+T[s+m+1], q);
}
Возможность использования приведенных алгоритмов для распознавания набора подстрок.