Порядок камеральной обработки полевых материалов горизонтальной съемки.

Вычисление координат производят в ведомости в следующем порядке:

1) вычисляют практическую сумму измеренных углов:

Σ β_пр. = β₁ + β₂ + β₃ + β₄ = 121⁰40,0ʹ + 99⁰04,0ʹ + 68⁰46,5ʹ + 70⁰28,0ʹ = 359⁰58,5ʹ,

где β_{1, 2, 3, 4} - горизонтальные углы;

 

2) определяют теоретическую сумму углов по формуле:

Σ β_теор. = 180⁰(n – 2) = 180⁰(4 – 2) = 360⁰00ʹ,

где n – число измеренных углов;

 

3) вычисляют угловую фактическую невязку:

f_βпр. = Σ_βпр. – Σ_βтеор.= 359⁰58,5ʹ ‒ 360⁰00ʹ = ‒0⁰01,5ʹ;

 

4) устанавливают предельную допустимую угловую невязку:

f_βдоп. = ±1ʹ√n = ±1ʹ√4 = ±2,0ʹ;

 

5) полученную угловую невязку фактическую невязку ‒0⁰01,5ʹ поровну распределяют на 4 угла с обратным знаком, причем, если поправки во все углы не получаются одинаковые, то большие (на 0,1) вводят в углы, образованные короткими сторонами:

δ_β1-2 = 00,4ʹ

δ_β2-3 = 00,4ʹ

δ_β3-4 = 00,4ʹ

δ_β4-1 = 00,3ʹ;

 

6) контроль вычисления поправок:

Σ δ_β = ‒f_βпр. = 00,4ʹ + 00,4ʹ + 00,4ʹ + 00,3ʹ = ‒0⁰01,5ʹ;

 

7) вычисляют исправленные углы по формуле:

β_испр. = β_изм. ± δ_β,

β_1испр = 121⁰40,0ʹ + 00,4ʹ = 121⁰40,4ʹ

β_2испр = 99⁰04,0ʹ + 00,4ʹ = 99⁰04,4ʹ

β_3испр = 68⁰46,5ʹ + 00,4ʹ = 68⁰46,9ʹ

β_4испр = 70⁰28,0ʹ + 00,3ʹ = 70⁰28,3ʹ,

где β_изм. – соответствующий точке угол, а исправленный угол – алгебраическая сумма угла и поправки.

Контроль вычисления исправленных углов:

Σ β_испр. = Σ β_теор.= 121⁰40,4ʹ + 99⁰04,4ʹ + 68⁰46,9ʹ + 70⁰28,3ʹ = 360⁰00ʹ

Σ β_испр. = Σ β_теор. = 360⁰00ʹ

 

8)вычисляют дирекционные углы по формуле:

α_2-3 = α_1-2 + 180⁰ – β_2испр;

α_3-4 = α_2-3 + 180⁰ – β_3испр;

α_4-1 = α_3-4 + 180⁰ – β_4испр;

α _2-3 = 75⁰15,0′+180 ⁰- 99⁰04,4′= 156⁰10,6′

α _3-4=156⁰10,6′+ 180 ⁰- 68⁰46,9′= 267⁰23,7′

α _4-1=267⁰23,7′+ 180 ⁰ -70⁰28,3′= 376⁰55,4′

 

Для контроля вычисления дирекционных углов следует найти дирекционный угол

α_{1 –2} по дирекционному углу α_{4 – 1} последней стороны и исправленному при вершине 1:

α_конеч. = α_4-1 + 180⁰ – β_1испр.

α _конеч = 376⁰55,4′+180 ⁰ – 121⁰40,4′=435⁰15,0′;

Это вычисленное значение должно совпадать с заданным дирекционным углом α_1-2. Если при вычислении уменьшаемое окажется меньше вычитаемого, к уменьшаемому прибавляют 360⁰. Если дирекционный угол получится больше 360⁰, из него вычитают 360⁰:

α_конеч. = 435⁰15,0′ - 360⁰00ʹ = 75⁰15,0ʹ;

 

9) вычисляют румбы. Контролем вычисления румбов является вычисление второй раз по тем же значениям.

α_1-2 = 75⁰15,0′ - 1 четверть СВ, r_1-2 = α_1-2 = СВ: 75⁰15,0′

10) вычисляют приращения координат по формулам:

ΔХ = d cosα

ΔУ = d sinα;

 

α _1-2 =75⁰15,0′ r_1-2=СВ: 75⁰15,0′; d _1-2 = 167,58 м;

Δ Х = + 167,58 × cos 75⁰15,0′ = + 42,67 м;

Δ У = + 167,58 × sin 75⁰15,0′ = + 162,06 м.

α _2-3 =156⁰10,6′ r_2-3= ЮВ:23⁰49,4′ d_2-3 =139,35 м;

Δ Х = + 139,35 × cos 23⁰49,4′= -127,48 м;

Δ У = + 139,35 × sin 23⁰49,4′= + 56,29 м.

α _3-4=267⁰23,7′ r_3-4= ЮЗ:87⁰23,7′ d_3-4 =247,93 м;

Δ Х = + 247,93 × cos 87⁰23,7′= -11,27 м;

Δ У = + 247,93 × sin 87⁰23,7′= -247,67 м.

α _4-1=16⁰55,4′ r_4-1= СВ:16⁰55,4′ d_4-1 =100,39 м;

Δ Х = + 100,39 × cos 16⁰55,4′=+96,04 м;

Δ У = + 100,39 × sin 16⁰55,4′= +29,22 м.

 

11) вычисляют невязки в приращениях координат замкнутого теодолитного хода:

f_Δх = Σ ΔX_пр – Σ ΔX_теор

f_Δу = Σ ΔY_пр – Σ ΔY_теор;

Так как в замкнутом ходе Σ ΔX_теор = 0; Σ ΔY_теор = 0.

где Σ ΔX_пр. – сумма приращения, Σ ΔY_пр. – сумма приращения, то

f_Δх = Σ ΔX_пр;

f_Δу = Σ ΔY_пр;

f_Δх = Σ ΔX_пр = ΔХ(+)+ΔХ(‒)=138,71-138,75= -0,04

f_Δу = Σ ΔY_пр = ΔY(+)+ΔY(‒)=247,57-247,67 = -0,10;

 

12) вычисляют абсолютную линейную невязку по формуле:

f_абс = ± ;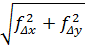

 

13) определяют относительную невязку по формуле:

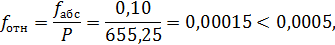
где P = 655,25 – периметр, сумма всех сторон хода.

 

14) полученные невязки f_Δх = ‒0,10 и f_Δу = ‒0,03 разделяют поровну по вычисленным приращениям координат пропорционально длинам сторон с обратным знаком:

δ_х1 = +0,01 м

δ_х2 = +0,01 м

δ_х3 = +0,01 м

δ_х4 = +0,01 м

δ_у1 = +0,03 м

δ_у2 = +0,03 м

δ_у3 = +0,02 м

δ_у4 = +0,02 м

 

15) контроль вычисления поправок:

∑ δ_х = ‒f_Δх = 0,01+0,01+0,01+0,01 м

∑ δ_у = ‒f_Δу = 0,03+0,03+0,02+0,02 м;

 

16) вычисляют исправленные приращения по формуле:

ΔХ_испр. = ΔХ_выч. ± δх_i ;

ΔХ_1испр. = ΔХ_выч. ± δх₁ = 42,67+0,01 =42,68м

ΔХ_2испр. = ΔХ_выч. ± δх₂ = - 127,48+0,01=-127,47 м

ΔХ_3испр. = ΔХ_выч. ± δх₃ = -11,27+0,01=-11,26 м

ΔХ_4испр. = ΔХ_выч. ± δх₄ = 96,04+0,01=96,05 м

ΔУ_испр. = ΔУ_выч. ± δу_i ,

ΔУ_1испр. = ΔУ_выч. ± δу₁ = 162,06+0,03=162,09 м

ΔУ_2испр. = ΔУ_выч. ± δу₂ = 53,29+0,03=56,32 м

ΔУ_3испр. = ΔУ_выч. ± δу₃ = -247,67+0,02=-247,65 м

ΔУ_4испр. = ΔУ_выч. ± δу₄ = 29,22+0,02=29,24 м

 

17) контроль вычисления приращений:

Σ ΔХ_испр = 0

Σ ΔХ_испр = 42,68-127,47-11,26+96,05= 0

Σ ΔУ_испр = 0

Σ ΔУ_испр = 162,09+56,32-247,65+29,24= 0

 

18) вычисляют координаты точек по формулам:

Х_i = Х_{i -1} + ΔХ_{(i–1) – i испр;}

У_i = У_{i -1 +} ΔУ_{(i -1) – i испр}

X₁ = 750,00 м;

X₂ = X₁ + ΔХ_{1-2 испр} = 750,00+42,68= 792,68 м

X₃ = X₂ + ΔХ_{2-3 испр} = 792,68-127,47=665,21 м

X₄ = X₃ + ΔХ_{3-4 испр} = 665,21-11,26=653,95 м

Y₁ = 950,00 м

Y₂ = Y₁ + ΔУ_1-2испр = 950,00+162,09=1112,09 м

Y₃ = Y₂ + ΔУ_2-3испр = 1112,09+56,32= 1168,41 м

Y₄ = Y₃ + ΔУ_3-4испр = 1168,41-247,65=920,76 м.

 

19) контролем служит получение заданной координаты точки 1 с помощью вычисления ее через координату точки 4 и исправленное приращение 4 – 1:

Х₁ = Х₄ + ΔХ_{4-1 испр} = 653,95+96,05=750,00 м

У₁ = У₄ + ΔУ_{4 – 1 испр} = 920,76+29,24=950,00 м

 

1.2.Составление горизонтального плана участка местности по результатам обработки ведомости замкнутого теодолитного хода и абрису горизонтальной съемки

На листе формата А1 при помощи линейки Дробышева строим сетку квадратов 10×10 см в масштабе 1:1000. Оцифровать сетку квадратов надо так, чтобы теодолитный ход оказался в центре листа.

Нанесение на план точек теодолитного хода производится по их вычисленным координатам. Для этого сначала определите квадрат сетки, в котором должен находиться пункт. Точка №1 с координатами Х =750,00 м и У=950,00 м попадает в квадрат сетки 700-900. От линии сетки Х=700 точка №1 отстоит на 750,00 - 700=50,00м. Поэтому от этой линии на двух вертикальных сторонах квадрата откладывают 50,00 м, что в масштабе составляет 5,00 см и проводят вспомогательную линию Х=750,00 м.

Далее на ней от линии У=1100 откладывают 50,00 м (950,00–900), что в масштабе составляет 5,00см. Полученная точка является местоположением точки №1 на плане.

Для точки №2 с координатами Х =792,68 м и У=1112,09 м попадает в квадрат сетки 700-1100. От линии сетки Х=700 точка №2 отстоит на 792,68 - 750=92,68 м. От этой линии на двух вертикальных сторонах квадрата откладывают 92,68 м, что в масштабе составляет 9,27 см и проводят вспомогательную линию Х=792,68 м. Далее на ней от линии У=1100 откладывают 12,09 м (1112,09–1100), что в масштабе составляет 1,21см. Полученная точка является местоположением точки №2 на плане. Правильность нанесения на план двух соседних точек проверьте по длинам сторон хода. Для этого на плане измерьте расстояния между вершинами хода и сравните их с соответствующими горизонтальными проекциями сторон, взятыми из ведомости вычисления координат; расхождение не должны превышать 0,2 мм на плане, т. е. графической точности масштаба. Горизонтальное проложение между точками 1 и 2 равно 167,58 м.

Точка №3 с координатами Х =665,21 м и У=1168,41 м попадает в квадрат сетки 600-1100. От линии сетки Х=600 точка №3 отстоит на 665,21- 600=65,21 м.Поэтому от этой линии на двух вертикальных сторонах квадрата откладывают 65,21 м, что в масштабе составляет 6,52 см и проводят вспомогательную линию Х=665,21 м. Далее на ней от линии У=1100 откладывают 68,41 м (1168,41 –1100), что в масштабе составляет 6,84 см. Полученная точка является местоположением точки №3 на плане. Горизонтальное проложение между точками 2 и 3 равно 139,35 м.

Точка №4 с координатами Х =653,95 м и У=920,76 м попадает в квадрат сетки 600-900. От линии сетки Х=600 точка №3 отстоит на 653,95- 600=53,95м. Поэтому от этой линии на двух вертикальных сторонах квадрата откладывают 53,95 м, что в масштабе составляет 5,40 см и проводят вспомогательную линию Х=653,95 м. Далее на ней от линии У=900 откладывают 20,76 м (920,76 –900), что в масштабе составляет 2,08 см. Полученная точка является местоположением точки №4 на плане. Горизонтальное проложение между точками 3 и 4 равно 247,93 м.

Горизонтальное проложение между точками 4 и равно 100,39 м.

Нанесение на план ситуации выполняют от сторон и точек теодолитных ходов согласно абрису съемки в масштабе 1:1000. При накладке ситуации на план расстояния откладывают при помощи циркуля-измерителя и масштабной линейкой, а углы – геодезическим транспортиром. При нанесении точек, заснятых способом перпендикуляров, перпендикуляры к сторонам хода восставляют прямоугольным треугольником. По мере накладки точек на план по ним в соответствии с абрисом вычерчивают предметы местности и контуры и заполняют их установленными условными знаками. Вдоль линии 1 – 2 идет грунтовая дорога шириной 6 м. От линии 1 – 4 по ходу часовой стрелки откладывают угол 74⁰21ʹ и по этому направления откладывают расстояние L = 90,25 м в масштабе (90,2 мм). Аналогично получают электрический столб от линии 1 – 2. По линии 3 – 4 сняты теплосеть, углы забора и люки с началом отсчета в точке 3. Улицу строителей с асфальтовым покрытием наносим по 4-м точкам, водопровод – по 2-м от линии 2 – 3 с началом отсчета в точке 2. Здание школы наносим по обмерам.

 

 

_.