В курсе мы рассматриваем системный анализ в качестве инструмента исследования ИС, а вернее комплект инструментов научных исследований и решения задач создания и внедрения информационных технологий (ИТ) в управленческую деятельность. Существуют два вида инструментов:
- неформальные методы;
- формальные методы.
Каждая из этих групп может быть подвергнута дальнейшему дроблению, однако на этом этапе мы не будем углубляться, а остановимся на ее верхнем уровне.
Неформальные методы системного анализа преимущественно концентрируются на решении задач организации аналитической деятельности. Здесь используются методики, широко привлекающие знания, накопленные в отрасли гуманитарных наук. По мере развития средств вычислительной техники эта отрасль системного анализа получила в свое распоряжение мощные средства хранения и представления знаний, работающие, в том числе и в псевдо-трехмерном режиме отображения, средства телекоммуникационного обеспечения аналитической деятельности и иные инструменты, способствующие интенсификации интеллектуального труда.
К числу неформальных методов относят:
- методы мозгового штурма;
- методы модерирования рабочих сессий и игротехники;
- методы экспертного анализа;
- метод Дельфи;
- метод сценариев;
методы классификации и структуризации проблемной области
* методы компактного представления данных (диаграммы и т. д.);
* методы календарного планирования и иные.
Формальные методы системного анализа являют противоположность неформальным; оперируя строгой математической символикой, они мало походят на неформальные методы. Абстрактные математические построения являются выражением сущности процессов, обеспечивая прогнозируемую точность и высокую объективность результатов исследования. Однако переход от неформальных методов к формальным методам является результатом эволюции знаний о системе.
Формальные методы также именуются методами формализованного представления систем и включают в себя:
* аналитические методы;
* вероятностные и статистические методы;
* теоретико-множественные и логические методы;
* лингвистические и семиотические методы;
* графические и иные методы.
Системный анализ сочетает в себе использование неформальных и формальных методов анализа и синтеза. Это сочетание достигается использованием таких системных теорий, как неформальный системный анализ и прогностика (ориентированные на применение процедур эвристического характера, основывающихся на личном и социальном опыте аналитика), теория выбора и принятия решений (основывающаяся на теории предпочтений или полезности), теория сложных систем и многомодельных исследований, синергетика и теория иерархических систем, теория больших систем (основывающаяся на формальных процедурах агрегирования и декомпозиции).
Исследование альтернативных стратегий, как правило, производится на моделях (увы, не всегда это возможно, да и не всякий руководитель в состоянии оценить преимущества моделирования перед непосредственным действием. (Привести пример с R3). Как правило, для решения задач многокритериального оценивания требуется использовать несколько разнородных моделей, отражающих различные аспекты поведения системы и ее элементов.
Моделирование. На этапе моделирования модель используется как инструмент исследования. То есть, модели полагаются адекватными. Модели используются в качестве систем, замещающих заданные фрагменты реальности - на них проводятся вычислительные и логические операции, выражающие выявленные на предшествующих этапах отношения и зависимости, определяются значения критериев выбора, обеспечивающие возможность сопоставления альтернативных стратегий. Речь идет о вариации исходных параметров и логики, отображающей стратегию управления. В результате чего формируется блок исходных данных, включающих значения и оценки критериев выбора, рисков и т.п. данных, используемых на заключительном этапе.
Можно говорить о существовании некоего обобщенного алгоритма проведения системно-кибернетического исследования, относительно которого могут допускаться незначительные отклонения, но в целом, сохраняющем свою структуру для большинства приложений системного анализа. Алгоритм, приблизительно отображающий схему проведения системно-кибернетического исследования, представлен на рисунке 5.

Рисунок 5 - Алгоритм проведения системно-кибернетического
исследования
Можно рассматривать различные аспекты подобия между моделью и фрагментов реального мира:
- физическое подобие, когда модель и объект имеют близкую физическую сущность;
- функциональное подобие, когда сходны их функции;
- динамическое подобие, проявляющееся в сходстве динамики изменения состояния объекта;
- топологическое подобие, проявляющееся в сходстве пространственной (в широком смысле, в том числе - организационной) структуры и иные.
Степень формализации моделей может варьироваться в широких пределах: от моделей, не подвергнутых процедурам формализации, до моделей строго формальных. Выбор формальных средств, используемых для представления моделей, не является произвольным и определяется двумя аспектами - компонентами модели:
- моделью интерпретации или интерфейсным компонентом (характеризующим процесс двунаправленного взаимодействия с потребителем, в роли которого может выступать как человек, так и автоматизированная система, реализующая функции ввода и считывания данных);
- сущностным компонентом (характеризующим специфику моделируемого фрагмента реальности, закономерности его функционирования, структуры и т. п.).
Если взглянуть на любую модель с точки зрения, характерной для специалиста в области разработки программного обеспечения, знакомого с объектным подходом к программированию, то модель предстанет в виде совокупности инкапсулированных (помещенных одна в другую) моделей. При этом модель интерпретации (адаптации, интерфейса) представляет собой внешнюю оболочку модели, а сущностная модель фрагмента реальности (объекта, процесса явления и т. п.) заключена внутрь. Часто модель интерпретации именуют метамоделью или, применительно к информационным технологиям, метаданными (так обстоит, например, с метаданными баз данных).
В отличие от простых - одноуровневых - моделей, сложные модели имеют несколько уровней вложенности, и на каждом уровне вложенности может существовать несколько разнородных моделей.
Наиболее значимые факторы, оказывающие влияние на выбор адекватной степени детализации модели это:
- назначение модели и цель исследования (аналитическая, прогностическая модель и т.д., исследовательская (научная) модель, кибернетическая (управленческая) модель);
- избирательность исследования (выражению средствами модели подлежит система или процесс в целом или их отдельные аспекты);
- степенью полноты знаний о системе или процессах, подлежащих моделированию;
- динамические характеристики моделируемой системы/процесса;
- структура моделируемой системы;
- условия наблюдаемости (непрерывное, кусочно-непрерывное, дискретное);
- характеристика среды и параметры возмущающих воздействий;
- время, доступное для синтеза модели/производства вычислений;
- динамические и точностные характеристики системы сбора информации (точность результатов не может быть выше точности измерений);
- динамические и точностные характеристики системы управления (чаще всего, нет смысла анализировать динамические и статические параметры системы или процесса, если отсутствуют средства управления, обеспечивающие необходимую скорость и точность доведения управляющих воздействий)
- точностные характеристики методов, используемых для обработки данных;
- характеристики платформы, используемой для реализации модели (в случае применения специальных технологических средств, например - ЭВМ);
- точностные характеристики реализации методов, с учетом ограничений технологической платформы, используемой их реализации и иные.
Приведенный перечень, несмотря на его громоздкость, нельзя назвать исчерпывающим, однако уже и его достаточно для понимания того, что модель должна удовлетворять целому ряду требований, а процесс моделирования не является процессом сугубо абстрактным, отвлеченным. По существу, на этапе синтеза модели решаются те же самые задачи системного исследования, но применительно к задаче построения модели, обеспечивающей решение задач следующего уровня. Так же, как и в иных случаях производится анализ объективных и субъективных ограничений, определяются оптимальные значения параметров, но не системы, а ее модели.
Процесс синтеза модели может быть представлен как процесс постепенного повышения уровня формализации и поэтапного продвижения в иерархии знаний следующего вида:
- гипотеза, предположение;
- теория, концепция;
- закономерность;
- закон.
Отсутствие достаточного объема знаний о системе не позволяет построить модель более высокой степени формализации, нежели вербальная или логико-лингвистическая модель типа сценария. Такая ситуация возникает тогда, когда причинно-следственные отношения не выявлены, структура системы и отношения между компонентами установлены лишь частично и подлежат уточнению, что соответствует знаниям уровня гипотезы или теории в предложенной иерархии.
Однако на практике ч аще встречается ситуация, когда некоторая формальная система позволяет адекватно описывать феномены различного происхождения - так обстоит дело со многими математическими формальными системами, полученными в результате развития естественнонаучных дисциплин (таковы дифференциальное, интегральное исчисление, теория множеств и иные).
Рассмотрим основные приемы и методы формализации предметной области исследований.
Вербальные или понятийные модели. С этапа синтеза вербальной модели начинается процесс поэтапной формализации системы и вербальная же (в большинстве случаев) модель формируется на заключительном этапе функционирования модели. Это вызвано тем, что формализм вербальной модели легко воспринимается широким классом потребителей, а синтез вербальной модели (по крайней мере, в первом приближении) может быть осуществлен и специалистом, не обладающим специальными навыками в области построения формальных моделей. Вербальные модели обладают наивысшей выразительной способностью и часто используются как инструмент интеграции формальных моделей и результатов их применения.
Вербальные модели создаются для:
1) получения на материальном носителе вербального описания:
- структуры системы;
- отношений между элементами;
- функций системы и ее компонентов;
- динамических параметров системы;
- проблемной ситуации;
- совокупности целей и задач деятельности;
- разнообразных ограничений (в том числе - по ресурсам);
- характеристик среды функционирования и возмущающих воздействий;
- формирования массива исходных данных, используемых на этапе структурирования и формализации знаний о системе;
- выявления специфики тезауруса, применяемого в данной предметной области (для внешнего эксперта), и упорядочения системы понятий, подлежащих выражению формальными средствами;
- выявления неполноты системы знаний и организации процесса их пополнения, как за счет внутренних ресурсов системы, так и с привлечением внешних информационных ресурсов;
- установления характера неопределенностей, с которыми придется столкнуться на этапе синтеза формальной модели;
- поиска базовых закономерностей и аналогий в смежных отраслях, которые могут быть использованы в дальнейшем.
Вербальная модель - это не обязательно исключительно текстовый документ - она может содержать, в том числе, и количественные характеристики, элементы структуризации (например, таблицы, схемы и графики).
Важным этапом вербального моделирования является этап приведения (стандартизации) терминологии и сокращения избыточности описаний. Результатом выполнения этой процедуры является вербальная модель, построенная в едином стандартизованном тезаурусе, дальнейшее использование которой упрощает решение задач автоматизации процессов анализа и перевода модели на следующий уровень формального представления.
Так, при решении задачи синтеза баз данных и систем информационного обеспечения деловых процессов, данных, полученных на этом этапе, зачастую оказывается достаточно для синтеза макета информационной системы.
При создании новых ИС (на стадии разработки вариантов концепции системы) создается вербальная модель архитектуры предприятия и информационной системы. Использование понятия архитектура предприятия позволяет устанавливать связь между бизнесом предприятия и параметрами ИС – функциями системы и интероперабельностью данных (возможность использования данных приложениями). Основное требование в том, чтобы любая информация, создаваемая в ИС, была независима от программного обеспечения разработки. Основное внимание должно быть сосредоточено на использовании Internet и Web -стандартов, языка XML, порталов, Web-сервисов, а также увеличении использования услуг провайдеров приложений.
Архитектура предприятия является компонентом стратегического планирования, гарантирующим на стратегическом уровне согласованность развития ИТ и стратегического развития предприятия. Она содействует совместному использованию информации между разными предприятиями, а также в государственных учреждениях, обеспечивая межведомственное взаимодействие.
Архитектура предприятия обычно имеет следующие слои (рис. 6):
1) бизнес-слой;
2) архитектура данных;
3) интеграция физических данных;
4) концептуальная модель/модель процессов;
5) архитектура приложений;
6) технологическая архитектура;
7) техническая модель

Рисунок 6 - Модель архитектуры предприятия
Бизнес-слой идентифицирует функции, процессы, организацию и информационные потоки, обеспечивающие миссию организации. Он представляет исходную точку зрения для анализа данных, используемых приложений и их возможностей, а также реализацию технологий, необходимых для поддержания повторного использования компонентов и выполнения стандартов. В этом слое учитываются все потенциально возможные методы доступа к информации (персональные контакты, электронные средства, бумажные документы, сервис-провайдеры).
Архитектура данных определяет главные типы данных, которые необходимы для поддержки деятельности предприятия. Содержит словарь общих данных и определений, который особо важен для использования. В архитектуру данных включаются не только операционные, но и аналитические данные, содержание, представленное на Web -сайтах, присутствует модель интероперабельности (поддержки взаимодействия).
Архитектура безопасности предусматривается для каждого компонента модели интероперабельности, начиная от услуг электронной аутентификации и заканчивая управлением доступом через запрашивающие приложения и транзакционные услуги. Секретность, как безопасность, отражается во всех компонентах модели интероперабельности.
Архитектура прило жений определяет используемые приложения и средства, предназначенные для эффективного управления данными и информацией, для поддержки деятельности и достижения намеченных целей.
Технологическая архитектура определяет доступное компьютерное оборудование, программное обеспечение, а также физическое расположение с позиции поддержания приложений, данных, функций.
Техническая модель показывает, как взаимодействуют те или иные компоненты.
Архитектура информационной системы представляет собой детальное руководство, которое определяет основные, стандартные или типовые элементы ИТ - систем, их взаимосвязь, а также процессы управления ИТ-системой.
ИТ- архитектура подразделяется на набор областей верхнего уровня (доменов), описывающих отдельные компоненты ИТ- систем. В состав списка доменов входят следующие области:
1) управление приложениями;
2) управление данными;
3) управление информацией;
4) управление пользователями и их доступом;
5) сети и коммуникации;
6) платформы;
7) управление системами информационная безопасность и др.
Для каждой области определяются возможные технологии. Так, для домена управления данными могут быть реляционные СУБД, почтовые базы, файловые каталоги, продукты и версии продуктов. Для каждой области, технологии и продукта могут устанавливаться «требования соответствия», определяющие необходимость соблюдения тех или иных международных рекомендаций (RFC), стандартов, российских законодательных актов, например по применению сертифицированных средств, внутренних инструкций и т.п.
Все описание архитектуры представляется в виде гипертекстовой базы данных, что позволяет эффективно организовать процесс управления жизненным циклом отдельных документов, а также эффективно разграничить права доступа к некоторым разделам при сохранении целостности и единства описания.
Логико-лингвистические и семиотические модели.
По завершении этапа вербального моделирования информационной системы или процесса, при условии, что логическая компонента модели была успешно выделена (маркирована или акцентирована), становится возможен переход на следующий уровень - уровень логико-лингвистического моделирования.
Формализация затрагивает преимущественно логический аспект существования или функционирования моделируемой системы. При построении логико-лингвистических моделей широко используется символьный язык логики и формализм теории графов и алгоритмов. Наиболее распространенным способом формального представления логико-лингвистических моделей является граф. В роли вершин графа выступают атомарные (примитивные) или сложные утверждения на естественном языке или символы, их заменяющие. Связи могут маркироваться различным образом, в частности, дуги могут отображать наличие функциональных зависимостей и операционных связей.
Процедура преобразования данных в ЭВМ связана с процедурой организации вычислительного процесса (ОВП), поскольку программа преобразования данных поступает в оперативную память ЭВМ и начинает исполняться после предварительной обработки управляющими программами процедуры ОВП. Процедура преобразования состоит в том, что ЭВМ выполняет типовые операции над структурами и значениями данных (сортировка, выборка, арифметические и логические действия, создание и изменение структур и устройств данных и т.п.) в количестве и последовательности, заданных алгоритмом решения вычислительной задачи. На логическом уровне алгоритм преобразования данных выглядит как программа, составленная на алгоритмическом языке программирования. Программа преобразования данных состоит из описания типов данных и их структур, которые будут применяться при обработке, и операторов, указывающих какие типовые действия и в какой последовательности необходимо проделать над данными и их структурами.
Таким образом, управление процедурой преобразования данных осуществляется в первую очередь программой решения вычислительной задачи, и если решается автономная задача, то никакого дополнительного управления процедурой преобразования не требуется. Управление требуется, если информационная технология организуется для периодического решения комплекса взаимосвязанных функциональных задач управления, когда необходимо оптимизировать процедуру преобразования данных по критерию минимизации времени обработки данных, либо по критерию минимизации объема затрачиваемых вычислительных ресурсов. Первый критерий особенно важен в режиме реального времени, а второй – в мультипрограммном режиме.
Задачей управления процедурой преобразования данных является, с одной стороны, минимизация информационных потоков между памятью ЭВМ и процессами, с другой – исключение дублирования операций в комплексе функциональных программ.
Первая часть задачи может быть формализована, если структурировать программу на типы применяемых в ней операций, совокупности используемых в них данных (информационных устройств) и связи между ними. Тогда модель этой части задачи преобразования данных может быть представлена в виде двудольного графа, состоящего из множества узлов-операций, соединенных дугами с множеством узлов информационных устройств (рис.7).
Этот граф можно сделать раскрашенным, пометить различным цветом дуги, относящиеся к различным информационным элементам. Тогда задача минимизации информационных потоков будет состоять в разбиении раскрашенного графа на подграфы (модули), при котором минимизируется суммарное число дуг различного цвета, связывающих выделенные подграфы.
Широкое применение логико-лингвистические модели нашли в отрасли разработки программного обеспечения, управления корпоративными информационными ресурсами и многих других отраслях, где требуется определенный уровень формализации, представляющий единство строгости, интуитивной понятности и высокой выразительной способности моделей.

Рисунок 7 - Граф преобразования данных
Логико-смысловые модели позволяют формировать тематически связные описания различных аспектов проблемы (равно, как и проблемы в целом) и проводить структурный анализ проблемной области. Тематически связные описания получаются за счет выделения из общей совокупности когнитивных элементов логико-смысловой сети некоторых тех, которые непосредственно относятся к заданной тематике. В качестве примера применения логико-смыслового моделирования можно рассматривать гипертекстовые системы, получившие широкое распространение в глобальной телекоммуникационной сети Интернет.
Статистические, теоретико-вероятностные модели
Статистическая или теоретико-вероятностная модель (стохастическая модель) - это модель, в которой обеспечивается учет влияния случайных факторов в процессе функционирования системы, основанная на применении статистической или теоретико-вероятностной методологии по отношению к повторяющимся феноменам. Данная модель оперирует количественными критериями при оценке повторяющихся явлений и позволяет учитывать их нелинейность, динамику, случайные возмущения за счет выдвижения на основе анализа результатов наблюдений гипотез о характере распределения некоторых случайных величин, сказывающихся на поведении системы.
Важную роль в статистических моделях играют гипотезы о характере процессов смены состояний в моделируемой системе. Так, например, весьма интересный случай представляет собой гипотеза о «марковости» процессов. Если существует уверенность в марковости процесса, это существенно меняет представления о системе. Система может рассматриваться как «инерционная», в большой степени зависящая от текущего ее состояния и характера возмущающего воздействия. Методы статистического моделирования широко распространены в сфере стратегического планирования и управления.
Аналитические модели
Данный класс моделей обладает высочайшей степенью формализации описаний и применяется там, где закономерности протекания процессов и функционирования системы являются хорошо изученными, а сами процессы могут рассматриваться как детерминированные.
Аналитическое математическое моделирование - это вид моделирования, в ходе которого основная роль отводится аналитической математической модели, обладающей следующими особенностями:
- аналитическая модель строится на основе некоторой теории или научной гипотезы;
- модель описывает в целом определенный аспект моделируемой системы (процесс в системе) посредством различных математических конструкций (функций или функционалов, алгебраических или дифференциальных уравнений и т. д.);
- модель позволяет получать конечные результаты исследования в виде некоторых формальных соотношений, пригодных для производства количественного или качественного анализа.
Проведению аналитического моделирования может предшествовать построение концептуальной модели с целью установления того, какой именно теоретический аппарат целесообразно использовать для моделирования данной конкретной системы.
При организации обслуживания вычислительных задач на логическом уровне создается модель задачи обслуживания, которая может иметь как прямой, так и оптимизационный характер. При постановке прямой задачи данными являются параметры вычислительной системы (ВС), а решением – показатели эффективности организации вычислительных процессов (ОВП). При постановке оптимизационной задачи задаются требуемые показатели эффективности ОВП, и требуется определить параметры ВC.
В ВС моменты появления заданий являются случайными и случайным является момент окончания вычислительной обработки. Поэтому при проектировании ВС пользуются статистическими данными о среднем количестве поступающих заявок в единицу времени на обработку в ВС, а также о среднем времени решения одной задачи. Эти данные позволяют рассматривать процедуру организации ВП с помощью теории систем массового обслуживания.
Рассмотрим модель обслуживания вычислительных заданий, введя следующие предположения:
- в системе протекают Марковские случайные процессы;
- потоки событий (появление заданий, окончание их обработки) являются простейшими;
Простейший поток событий характеризуется стационарностью (независимость параметров во времени), ординарностью (события в потоке появляются поодиночке) и «беспоследствием» (появляющиеся события не зависят друг от друга).
- число заданий в очереди не ограничено, но конечно.
Обозначим состояния рассматриваемой системы:
S0 – в системе нет заданий;
S1 – в системе одно задание и оно обрабатывается на ЭВМ1;
Sn – в системе n заданий и они обрабатываются на ЭВМ1, ЭВМ2,..ЭВМ n;
Sn+1 – в системе (n +1) задание, n заданий обрабатываются на ЭВМ и одно задание стоит в очереди;
S n+m - в системе (n+m) заданий, n заданий обрабатываются на ЭВМ и m заданий стоят в очереди.
Рост числа заявок в системе происходит под воздействием их потока с интенсивностью λ, а уменьшение – под воздействием потока обслуживания с интенсивностью μ. Размеченный граф состояний системы приведен на рисунке 8.
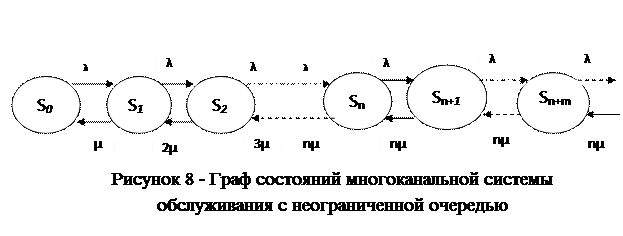
Увеличение числа одновременно работающих машин приводит к росту интенсивности обслуживания от μ до nμ. Дальнейший рост числа заявок переводит систему в состояние n +1, n +2,... n+m, а интенсивность потока обслуживания будет оставаться неизменной, равной nμ.
В процессе работы реальные вычислительные системы быстро достигают установившегося режима. Тогда вероятности состояний не будут зависеть от времени. Для вычисления финальных вероятностей используют систему дифференциальных уравнений Колмогорова, которые превращаются в систему алгебраических уравнений. На основе графа (рис.8) может быть записана следующая система алгебраических уравнений:
λP0 = μP1;
(1μ + λ)P1 = λP0 + 2 μP2;
(2μ + λ)P2 = λP1 + 3 μP3;
…………………………..
……………………….
(nμ + λ)Pn = λPn-1 + nμPn+1;
(nμ + λ)Pn+1 = λPn + nμPn+2;
……………………………….
(nμ + λ)Pn+j = λPn+j-1 + nμPn+j+1; j>=1.
Финальные вероятности состояний системы в результате решения системы уравнений описываются следующими уравнениями:

где P0 –вероятность состояния S0, при котором в системе заявок нет;
ρ=λ/μ – параметр системы, показывающий, сколько в среднем заявок приходит в систему за время обслуживания заявки одной ЭВМ (одним каналом обслуживания); Pi - вероятность состояния системы Si, i =1, 2,... n;
P n – вероятность того, что все ЭВМ заняты обслуживанием заявок;
P n+j – вероятность того, что все ЭВМ системы заняты обработкой заданий и j заявок стоят в очереди.
Приведенные формулы имеют смысл тогда, когда очередь конечна,
т.е. ρ/n < 1 или λ/nμ < 1.
Это выражение говорит о том, что в среднем число заданий, приходящих в вычислительную систему в единицу времени, должно быть, меньше числа обрабатываемых заданий в единицу времени всеми ЭВМ системы. При ρ/n >1 очередь растет до бесконечности и такая система не справится с потоком заданий. Появляются задания, ожидающие обработки вечно.
Основными показателями эффективности работы системы являются:
- среднее число занятых каналов (ЭВМ)

- среднее число заданий в очереди

- среднее число заданий в системе
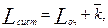
- среднее время пребывания задания в системе

- среднее время пребывания задания в очереди

Для уменьшения времени пребывания задания в системе, а значит и в очереди, требуется при заданной интенсивности потока заявок либо увеличивать число обслуживающих ЭВМ, либо уменьшить время обслуживания каждой ЭВМ, либо и то и другое вместе.
С помощью теории массового обслуживания можно получить аналитические выражения и при других дисциплинах обслуживания очереди и конфигурациях вычислительной системы.
Важным достоинством аналитического моделирования является возможность получения на его основе фундаментальных результатов и инвариантных зависимостей, которые могут быть распространены как на различные случаи использования моделируемой системы в тех или иных ситуациях и распространены на случаи рассмотрения других систем данного класса.
Основным же недостатком аналитического моделирования является то, что его применение к сложным системам требует существенной идеализации описания системы. Это связано с разрастанием объемов вычислений даже при несущественном усложнении описаний. Такая идеализация может приводить к неполной адекватности получаемых результатов, к тому, что эти результаты могут использоваться лишь в качестве первого приближения.
Имитационные модели
Имитационная модель - это комплексное логико-математическое представление системы, реализованное в виде программы, предназначенной для решения на ЭВМ, включающее в себя модели различного типа, и рассматривающее аспект функционирования динамической системы во времени. Данный класс моделей применяется при невозможности строгого аналитического решения задачи или проведения натурного эксперимента. Имитационные модели служат для изучения поведения во времени сложной неоднородной динамической системы, относительно структуры которой существуют точные знания или детализированные гипотезы.
Частным случаем имитационных моделей являются модели ситуационные. Ситуационные модели - это модели, используемые при решении задач с неопределенностью, исходя из совокупности ситуаций. Под ситуацией будем понимать временное отношение, сложившееся между ее объектами-участниками, либо между состояниями этих объектов.
Соответственно, под ситуационным моделированием будем понимать метод анализа некоторой системы с применением ситуационной модели, с требуемой степенью адекватности отображающую логическую, временную, пространственную структуру процессов, а также характер и структуру информации о состоянии системы и изменении образующих ее элементов.
Для создания ситуационных моделей требуется решить следующие задачи:
- создать информационную модель фрагмента реального мира, в которой каждому явлению, процессу или участнику будет соответствовать уникальный информационный аналог;
- обеспечить сбор и регистрацию информации об изменениях ситуации во времени, пространстве и пространстве введенных признаков оценить прогностический потенциал тех или иных ситуаций (что связано с инерционностью вовлеченных в ситуацию объектов и системы в целом и т. п.).
В целом структура ситуационной модели определяется субъективными особенностями восприятия и свойственным аналитику способом разложения ситуации на составляющие. Это вызвано тем, что эксперт-аналитик, осуществляющий процедуру синтеза ситуационной модели, формулирует свои собственные критерии, соответствующие пребыванию системы в том или ином состоянии.
Построение имитационной модели системы с целью проведения расчетов характеристик надежности начинается с изучения структурной схемы системы и стратегии ее функционирования. На основании структурной схемы строится надежностная схема системы, которая характеризует статическую составляющую системы. В качестве аппарата для представления схем системы используется аппарат теории графов. Элементы системы изображаются в виде вершин графа, связи между элементами - в виде дуг (рис. 9). После построения надежностной схемы системы в виде графовой модели ее необходимо представить в виде функциональной зависимости (формализованное представление структуры системы). При построении имитационных моделей для формализованного представления надежностной схемы системы рекомендуют использовать аппарат алгебры логики. Используя этот аппарат, вероятностные характеристики надежности системы, такие как вероятность отказа или вероятность безотказной работы, вычисляют через логические функции работоспособности.
Следующим этапом построения имитационной модели является отображение стратегии ее функционирования. На этом этапе осуществляется построение динамической составляющей модели системы. В качестве примера рассмотрим достаточно общую стратегию функционирования системы. Пусть в моменты времени Tk, 2Tt,..., nTk производятся контрольные мероприятия по проверке неисправности элементов системы. Если в момент проведения контроля исправности элементов обнаруживается отказ, то начинаются восстановительные мероприятия. Могут быть ситуации, когда при проведении контрольных проверок отказ не обнаруживается, и элемент простаивает в состоянии отказа до следующего момента контроля. Функционирование системы продолжается до момента времени Тр, если система не отказала, или до момента отказа. В момент времени Тр начинается плановая профилактика, в момент отказа системы начинается аварийная профилактика. После проведения профилактического обслуживания система полностью обновляется, и процесс функционирования начинается заново.
 Будем считать заданными периоды между проведением контрольных проверок Tk и период времени Тк, при достижении которого система подвергается восстановлению. Для организации процесса моделирования необходимо также задать вероятность обнаружения отказа Ро и исходные данные для моделирования отказов и восстановлений элементов, а именно, плотность распределе
Будем считать заданными периоды между проведением контрольных проверок Tk и период времени Тк, при достижении которого система подвергается восстановлению. Для организации процесса моделирования необходимо также задать вероятность обнаружения отказа Ро и исходные данные для моделирования отказов и восстановлений элементов, а именно, плотность распределе