ЛАБОРАТОРНАЯ РАБОТА 2
Методы усреднения и сглаживания временных рядов
Цель работы: научить пользоваться различными методами усреднения и сглаживания временных рядов.
1 Основные сведения
Достаточно простым методом выявления тенденции развития является усреднение или сглаживание временного ряда, т.е. замена фактических уровней расчетными, имеющими меньшие вариации, чем исходные данные. При наивных моделях строятся простые модели прогноза, в которых предполагается, что будущее лучше всего характеризуется последними событиями. Методы усреднения позволяют делать прогнозы, основываясь на среднем значении прошлых наблюдений. Методы сглаживания формируют прогноз, усредняя прошлые данные с учетом уменьшающихся весовых коэффициентов.
Рассмотрим кратко указанные методы.
Наивные модели. Чаще всего модель применяется в ситуации, когда "время жизни" фирмы еще незначительно: аналитики должны делать прогнозы на основе малого числа наблюдений. Вследствие того, что обычно методики прогнозирования требуют больших массивов исходных данных, подобная ситуация весьма проблематична для формирования прогнозных оценок. Здесь единственно возможный выход сводится к "наивному" прогнозу, при котором предполагается, что последний период лучше всего предсказывает будущее. Иначе говоря, наивным прогнозом для каждого временного периода является предшествующее ему наблюдение.
Методы усреднения
Простые средние. В этом методе для создания прогноза на следующий период используется среднее значение всех прошлых наблюдений. Метод простых средних применим в ситуациях, когда процессы, формирующие временные ряды, стабилизировались, а внешняя среда оказывает незначительное влияние на происходящий процесс. Как только новое наблюдение становится доступным, для прогнозирования на следующий период необходимо учесть и это наблюдение.
Скользящие средние. При использовании метода простого среднего прогнозирование выполняется на основе усреднения всех существующих данных. Но в некоторых случаях представляют интерес самые последние наблюдения. Тогда можно ограничиться только последними наблюдениями и зафиксировать число точек временного ряда, подлежащих усреднению. Важно отметить, что в этой методике используются только последние k наблюдений (k - ширина окна), а число точек усреднения не изменяется со временем. Здесь всем наблюдениям присваиваются одинаковые весовые коэффициенты, а каждое новое наблюдение включается в среднее по мере его появления при одновременном исключении наиболее старого.
Методы сглаживания
Экспоненциальное сглаживание (ЭС). По сравнению с методом скользящих средних, где учитываются только наиболее "свежие" данные, при ЭС используется взвешенное скользящее усреднение всех данных предыдущих наблюдений. ЭС предусматривает постоянное обновление модели за счет наиболее свежих данных. Метод основан на сглаживании временных рядов прошлых наблюдений при присваивании членам ряда определенных весов: последнему наблюдению придается вес α; предпоследнему - (1 – α); третьему от конца ряда - (1 – α)2 и т.д. В сглаженном виде новый прогноз для периода времени t +1 можно представить как взвешенное среднее последнего наблюдения в момент t и ее прежнего прогноза на этот же период t. Таким образом, ЭС - это старый прогноз с уточнением в виде произведения α на ошибку последнего прогноза. В данном методе принято, что 0 < α < 1. Постоянная сглаживания α является взвешивающим фактором. Ее реальное значение определяется тем, в какой степени текущее наблюдение должно влиять на прогнозируемую величину. При α→1 в прогнозировании существенно учитывается величина ошибки последнего прогноза. При малых значениях α прогнозируемая величина наиболее близка к предыдущему прогнозу.
Экспоненциальное сглаживание с учетом тренда. В ряде случаев данные наблюдений могут иметь заметный тренд, т.е. включают информацию, которая позволит учитывать возможные будущие изменения. В подобной ситуации необходима функция прогнозирования линейного тренда. При наличии во временном ряду тенденции к росту вместе с оценкой текущего уровня необходима и оценка наклона. В методике Хольта (Holt) значения уровня и наклона сглаживаются непосредственно; при этом используются различные постоянные сглаживания для каждого из них: α, β. Эти постоянные позволяют оценить текущий уровень и наклон, уточняя их каждый раз, когда появляются новые наблюдения. Как и при обычном ЭС, постоянные α, β выбираются субъективно или путем минимизации ошибки прогнозирования. Чем большие веса будут взяты, тем большему сглаживанию подвергаются данные. Меньшие веса делают структуру сглаженных значений менее ровной. Для минимизации ошибки прогноза нужно создать сетку значений α и β (т.е. все комбинации α = 0,1,..., 0,9 и β= 0,1,..., 0,9) и выбрать ту комбинацию, которая дает меньшую величину ошибки.
Экспоненциальное сглаживание с учетом тренда и сезонности. При наличии в структуре данных еще и сезонности, кроме тренда и уровня, используется трехпараметрическая модель Винтерса (Winters). Этот метод является расширением метода Хольта, и для учета сезонности вводится дополнительная постоянная сглаживания γ. Как и в предыдущем методе, веса α, β, γ выбираются субъективно или путем минимизации ошибки прогнозирования.
2 Работа на компьютере
Выполнение данной работы производится с программным пакетом Statistica; версия 6.1.
1. Выбрать файл Series_G из пакета: последовательно нажав Файл –Открыть, приходим к папке Datasets, в которой из папки Examples выделить файл Series_G (Ряд_G). Данные представляют собой ежемесячное количество пассажиров (в тысячах), перевезенных международными авиалиниями в 1949-1960 гг.
2. Войти в модуль временных рядов: нажав опцию Анализ и далеевыбрать Углубленные методы анализа - Временные ряды и прогнозирование. На экране отобразится стартовая панель Анализ временных рядов (рис.1).

Рис.1. Стартовая панель
Нажать на кнопку Переменные для входа в диалог. Поскольку Series G - единственная переменная в этом файле, она будет автоматически выбрана при открытии диалогового окна Анализ временных рядов.
3. Войти в диалоговое окно Экспоненциальное сглаживание и прогноз, для чего нажать соответствующую клавишу (рис.2).

Рис.2. Диалоговое окно
4.Выделить закладку Прогноз. Поскольку Series_G содержит даты в именах наблюдений, то нужно использовать их для меток на оси X графика. В окне Пометить точки на оси Х выбрать опцию Именами наблюдений. Затем выбрать опцию Масштаб оси х вручную и определить Mин = 1 и Шаг = 12 (так как в году 12 месяцев). Теперь необходимо нажать кнопку График в окне Просмотр выделенной переменной. На экране появится график временного ряда Series_G (рис.3).

Рис.3. Исходный временной ряд
Простое экспоненциальное сглаживание
5. Перейти к закладке Дополнительно и в окне Прогноз установить число 12, которое определяет прогноз на один полный год вперед. На этой же закладке выбрать опцию Простая и затем нажать кнопку ОК.Перейти к закладке Прогноз и в окне Просмотр нескольких переменных нажать кнопку График. Появится график с тремя кривыми: исходный и сглаженный ряды, а также ряд остатков (рис.4).
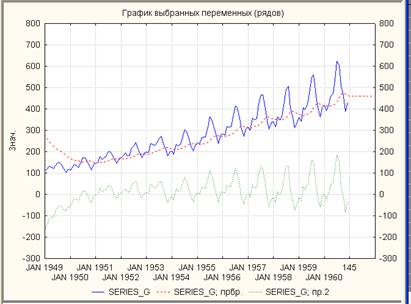
Рис.4. Результат экспоненциального сглаживания при α=0,1
Вид графиков позволяет выявить два факта. Во-первых, сглаженный ряд имеет линейный тренд, но в нем имеются и сезонные колебания. Во-вторых, все значения прогнозов одинаковы. На самом деле это легко объяснить. Каждое сглаженное значение или прогноз St вычисляется по формуле St = St- 1 + α *e, где e – ошибка, равная разности между наблюдаемыми и предсказанными (сглаженные или прогнозируемые) значениями. При вычислении прогнозов наблюдаемые значения отсутствуют, поэтому ошибкаравна 0. Таким образом, все прогнозы одинаковые.
Теперь рассмотрим значение сглаживающего параметра α. Из формулы, приведенной выше, ясно что, если α→ 0, то все сглаженные значения становятся очень похожими. Если α → 1, то сглаженные значения приближаются к исходным наблюдениям.
6. Установить параметрα = 0,9. На рис.5 в качестве примера показан результат сглаживания при этом значении параметра. Теперь сглаженные значения очень близки к наблюдаемым и отвечают ряду, сдвинутому на одно наблюдение вперед. В самом деле, при α = 1 каждое сглаженное наблюдение будет в точности равно предыдущему наблюдению. Поэтому α можно назвать параметром жесткости. Чем меньше α, тем "жестче" сглаженный ряд и в нем меньше воздействий случайных флуктуаций.
Оценить влияние α, варьируя этот параметр в диапазоне от 0 до 1 и наблюдая за изменением сглаживающей кривой.
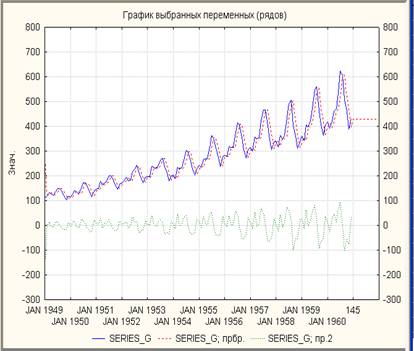
Рис.5. Результат экспоненциального сглаживания при α = 0,9