Лабораторная работа 5
Цель работы: ознакомить студентов с основными понятиями нечеткой логики и научить практическим навыкам разработки нечетких систем в среде Fuzzy Logic системы Matlab.
1 Теоретические основы нечеткой логики
1.1 Основные понятия нечеткой логики
Главная идея нечеткой логики (Fuzzy Logic) состоит в том, что интеллектуальный способ рассуждений, опирающийся на естественный язык общения человека, не может быть описан в рамках традиционных математических формул. Формальному подходу присуща строгая однозначность интерпретации, а все, что связано с применением естественного языка, имеет многозначную интерпретацию. Прилагательное «fuzzy», которое переводится на русский язык как «размытый», «ворсистый», «нечеткий», введено в название новой теории, чтобы разграничить ее с традиционной четкой математикой и аристотелевой логикой, оперирующих с четкими понятиями: «истина – ложь», «включено - не включено». Основатель современной концепции нечеткой логики профессор Л. Заде (L. Zaden) построил новую математическую дисциплину, в основе которой лежит не классическая теория множеств, а теория нечетких множеств. Последовательно проводя идею нечеткости, можно описать нечеткие аналоги всех основных математических понятий и создать аппарат нечеткой логики (НЛ) для моделирования человеческих рассуждений и способов решения задач.
Нечеткое множество - это формализация лингвистической информации для построения математических моделей. В основе этого понятия лежит представление о том, что составляющие данное множество элементы, обладающие общим свойством, могут обладать им в различной степени, и, следовательно, принадлежать к этому множеству с различной степенью.
Сущность НЛ сводится к следующим моментам:
- в ней используются лингвистические переменные (вместо обычных числовых) или в дополнение к ним;
- простые отношения между переменными описываются с помощью нечетких высказываний;
- сложные отношения определяются нечеткими алгоритмами.
Практическое использование НЛ предполагает наличие функций принадлежности (ФП), которыми описываются лингвистические переменные «малый», «средний», горячий» и т.д. Под ФП будем понимать кривую, указывающую, каким образом каждая точка входного пространства отображается в степень принадлежности между 0 и 1. Для нахождения ФП могут быть использованы различные методы, например: прямые; косвенные; посредством типовых форм; по данным эксперимента. Рекомендуется использовать типовые формы ФП, в частности, треугольные, трапециевидные, гауссовы и другие. Форма ФП определяется разработчиком системы, исходя из условий простоты, удобства и эффективности использования. Например, в модуле Fuzzy Logic системы Matlab, применяемого для решения задач посредством НЛ, имеется одиннадцать стандартных видов ФП.
1.2 Система нечеткого логического вывода
Нечеткий логический вывод - это аппроксимация зависимости «входы - выход» на основе лингвистических высказываний «если - то» и логических операций над нечеткими множествами. Типовая структура системы нечеткого вывода показана на рис.1.
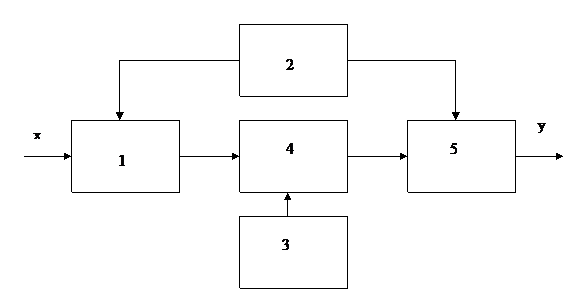
Рисунок 1 - Система нечеткого логического вывода
(1 – фаззификатор; 2 -функции принадлежности; 3 - нечеткая база знаний; 4 - машина нечеткого логического вывода; 5 - дефаззификатор)
Система логического вывода содержит следующие модули:
· фаззификатор - преобразует фиксированный вектор влияющих факторов Х в вектор нечетких множеств 
, необходимых для нечеткого вывода;
· функции принадлежности - используются для представления лингвистических термов в виде нечетких множеств;
· нечеткая база знаний - содержит информацию о зависимости Y = f ( X ) в виде лингвистических правил: если - то;
· машина нечеткого логического вывода - на основе базы знаний определяет значение выходной переменной в виде нечеткого множества 
, соответствующего нечетким значениям входных переменных ;
· дефаззификатор - преобразует выходное нечеткое множество в четкое число Y.
Ввиду важности базы знаний рассмотрим ее более подробно. Эта база задает взаимосвязь между входами и выходами исследуемого объекта в таком формате:
ЕСЛИ (посылка правила), ТО (заключение правила).
Посылка правила представляет собой утверждение типа «х есть малый», где «малый» - это терм, заданный нечетким множеством на универсальном множестве лингвистической переменной х. Заключение правила - это факт типа «у есть d », в котором значение выходной переменной может задаваться нечетким термом («у есть большой»), классом решений («у есть надежный заемщик»), четкой константой («у = 5»).
Многомерные зависимости «входы – выходы» задаются нечеткими правилами с логическими операциями И или ИЛИ. Нечеткую базу знаний, связывающую входы Х = (х1, х2,..., хn) с выходом у, представим следующим образом:
(1)
где 
- нечеткий терм, которым оценивается переменная хi в j -м правиле, 
; di - заключение j –го правила; m - количество правил в базе знаний; Θj - логическая операция (И или ИЛИ); 
- нечеткая импликация.
В машине нечеткого вывода часто используется логический вывод Мамдани, названный так в честь английского ученого, который впервые предложил нечеткий контроллер для модели парового двигателя. Этот вывод выполняется по базе знаний (1), в которой все значения входных и выходной переменных заданы нечеткими множествами. База знаний Мамдани может трактоваться как разбиение пространства влияющих факторов на подобласти с размытыми границами, внутри которых функция отклика принимает нечеткое значение. Правило в базе знаний представляет собой «информационный сгусток», отражающий одну из особенностей зависимостей «входы – выход».
В результате логического вывода по j – му правилу базы знаний получим нечеткое значение выходной переменной у. Результат логического вывода по всей базе знаний находят агрегированием нечетких множеств, т.е. посредством операции максимума всех выходных множеств.
Четкое значение выхода, соответствующее данному входному вектору, определяется путем дефаззификации суммарного выходного нечеткого множества. Наиболее часто применяется способ дефаззификации по методу центра тяжести, при котором четкий выход определяется как абсцисса центра тяжести фигуры, изображающей выходное нечеткое множество.
2 Работа на компьютере
2.1 Подключение виртуальной машины
Работа проводится на виртуальной машине (ВМ), на которой установлен программный модуль Fuzzy Logic системы Matlab, версия 7.01. Для подключения ВМ нужно сделать следующие шаги:
1. Диск D / Data (D:) / VMware MLab-FLt / Windows XP Professional / OK.
2. Ctrl –Alt –Insert
3. Пароль: ML
4. Matlab 7.01
5. Выключение (из окна виртуальной машины): Пуск / Завершение работы (не нажимая на крестик вверху справа).
2.2 Работа в системе Matlab
Схема работы с системой Matlab показана на рис.2.
Редактор входов
Рисунок 2 - Схема работы модуля Fuzzy Logic системы Matlab
1.Вход в модуль: после вызова системы Matlab в командном окне (Command Window) набрать слово fuzzy и нажать клавишу Enter. Появится окно редактора системы нечеткого вывода Fuzzy inference system (FIS) – editor (рис.3).
Рисунок 3 - Окно редактора
2. Для ознакомления с работой системы нечеткого вывода (СНВ) рассмотрим задачу о чаевых. Входными переменными являются качество еды и обслуживания, выходной переменной - размер чаевых официанту, назначаемый в процентах от величины счета.
По умолчанию редактор СНВ создает систему с одним входом и одним выходом; создаваемая система относится к типу Мамдани. Добавить второй вход, для чего в меню Edit выбираем команду Add variable - input (добавить переменную - вход). Появится окно редактора с двумя входами.
3. Переименовать входы и выход. Щелчком мыши выделить окно с первой переменной Input1, затем в окне редактора вместо Input1 набрать food (еда) и нажать Enter. Аналогичные процедуры произвести со вторым входом (обозначим его как service) и выходом (tip - чаевые). В результате должно получиться окно редактора с двумя входами, одним выходом и соответствующими новыми подписями переменных (рис.4).
Рисунок 4 - Окно редактора с двумя входами и одним выходом
4. Cохранить файл (если нужно), присвоив ему то же название, что и выходной переменной: tip. Для этого в окне редактора нажать File – Export to disk (отправить на диск) и набрать tip вместо прежнего наименования Untitled (безымянный). В этом случае данные сохраняются до окончания сеанса работы с системой Matlab.
5. Задать функции принадлежности (ФП) можно двумя способами:
· через меню Edit - Membership Functions (редактирование ФП);
· двойным щелчком по окну соответствующей переменной.
Установить диапазон изменений для первой переменной [0 10] в полях Range, Display Range (диапазон, отображение диапазона). Достаточно набрать [0 10] в первом окне, после чего нажать Enter, и требуемый диапазон появится в двух окнах.
Далее произвести редактирование ФП, для чего через меню Edit – Add MFs (добавить ФП) и в появившемся окне Membership Functions выбрать тип ФП (примем для первой переменной гауссов тип (gaussmf) и их количество, равное 3.
Присвоить имена трем ФП: плохая, хорошая, превосходная (bad, good, excellent). После переименования каждой из ФП необходимо нажать Enter (рис.5).
Рисунок 5 - Функции принадлежности для первой переменной
Аналогичную процедуру произвести для второй входной переменной service, установив для нее диапазон таким же, как и для первой переменной, но выбрав в качестве двух ФП трапеции (trapmf). Параметры трапеций установить в соответствующем окне, равными (0 0 1 3) и (7 9 10 10), присвоив наименования ФП: медленное (slow) и быстрое (quick) (рис.6).
Рисунок 6 - Функции принадлежности для второй переменной
Такая же последовательность действий нужна и для выходной переменной, где нужно задать диапазон от 0 до 25 процентов, выбрать три ФП треугольного типа (trimf) с параметрами (0 5 10), (5 12,5 20), (15 20 25) и наименованиями small, middle, big (рис.7).
Рисунок 7 - Функции принадлежности для выходной переменной
6. Создать базу правил через меню Edit - Rules (редактирование правил) следующего типа, например:
· Если еда - плохая или обслуживание - медленное, то чаевые - малые.
· Если еда - превосходная и обслуживание - быстрое, то чаевые – большие.
Добавить самостоятельно 1-2 правила. Обратить внимание на то, что непосредственно ничего набирать не надо: в окне редактора необходимо только отметить выбранные позиции.
После каждого правила нужно нажать Add rule (добавить правило) в нижней части окна. В скобках после каждого правила указан вес правила (по умолчанию принимается равный 1). База правил показана на рис.8.
Рисунок 8 - База правил системы нечеткого вывода
7. Провести моделирование работы созданной системы оценки чаевых, для чего через меню View –Rules (просмотр правил) выйти на систему графических окон, расположенных по строкам и по столбцам. Количество строк равно числу правил, а число столбцов - числу входных и выходной переменных. Кроме того, в дополнительном окне отображается суммарное выходное нечеткое множество, из которого путем дефаззификации определяется четкое значение выхода (в нашем случае - размера чаевых). Путем перемещения мыши по диапазонам входных переменных убедиться в работоспособности системы (рис.9 и 10).
Рисунок 9 - Оценка чаевых при плохой еде и медленном обслуживании (размер чаевых равен 5% от счета)
Рисунок 10 - Оценка чаевых при превосходной еде и быстром обслуживании (размер чаевых равен 18% от счета)
8. Построить трехмерные графики через меню View - Surface и провести их анализ (рис.11).
Рисунок 11 - Трехмерный график зависимости выходной переменной от входных факторов
Варианты заданий
Вариант 1. Оценка риска при выдаче кредита физическому лицу
Входные переменные: возраст клиента (годы), доход (доллар), квартира (баллы), автомобиль (баллы), дача (баллы).
Выходная переменная: величина кредитного риска.
Вариант 2. Оценка риска инвестиционного проекта
Входные переменные: длительность выполнения проекта (годы), объем вложенных средств (доллары), качество разработки проекта (хорошее, плохое), положение в стране, куда вкладываются инвестиции (стабильное, нестабильное).
Выходная переменная: величина инвестиционного риска.
Вариант 3. Туристская фирма, въездной туризм в России. Оценка риска нового разрабатываемого туристского маршрута
Входные переменные: ситуация в России (стабильная, нестабильная), погодные условия (плохие, средние, хорошие), контингент туристов по возрасту (до 25 лет, 25 – 50, выше 50), стоимость тура (500 – 1500 $).
Выходная переменная: риск туристской фирмы.
Вариант 4. Продажа квартир в строящемся доме
Входные переменные: площадь квартиры (кв.м), расстояние до станции метро (близкое, среднее, далекое), этаж, на котором находится квартира, стоимость квартиры ($).
Выходная переменная: риск непродажи квартир в новом доме.
Примечание. Варианты заданий могут быть дополнены как преподавателем, ведущим занятия, так и самими студентами применительно к их курсовым или дипломным работам.