ПРОВЕРКА ГИТОТЕЗЫО ЗАКОНЕ РАСПРЕДЕЛЕНИЯ
Выполнил студент
Группы ОД 10А1
Стегасов А.О.
Принял: Мирошниченко Т. П.
Омск - 2011
Исходные данные
В-17
Определение: Математическую статистику определяют как науку о методах получения и обработки результатов наблюдений (измерений) для установления закономерностей в массовых случайных явлениях.
Задачи математической статистики: на основании экспериментальных данных построить теоретико-вероятностную модель изучаемых явлений.
Пусть требуется изучить случайную величину х распределенную по некоторому неизвестному нам закону, множество значений случайной величины х называют генеральной совокупностью. Генеральная совокупность может содержать конечное или бесконечное число элементов. Отобранная из генеральной совокупности множество отдельных значений случайной величины х распределенные по определенному закону называются выборкой объема n.
Вариант №17
Дана выборка из генеральной совокупности случайной величины Х.
Требуется:
1) построить гистограмму(многоугольник относительных частот) и выдвинуть гипотезу о законе распределения случайной величины Х;
2) проверить эту гипотезу по критерию Пирсона (уровень значимости выбрать самостоятельно);
3) найти доверительные интервалы для математического ожидания и дисперсии (доверительную вероятность выбрать самостоятельно).
| 19,1 | 18,4 | 18,7 | 18,4 | 19,2 | 18,8 | 18,9 | 18,7 | 18,6 | 20,0 |
| 19,0 | 20,6 | 20,3 | 22,2 | 18,3 | 21,8 | 18,3 | 19,8 | 18,6 | 19,1 |
| 18,8 | 18,3 | 19,4 | 19,5 | 18,6 | 20,9 | 19,1 | 18,4 | 18,6 | 18,5 |
| 18,7 | 20,4 | 24,9 | 19,4 | 20,0 | 20,5 | 20,2 | 18,9 | 19,0 | 20,4 |
| 19,7 | 18,3 | 18,5 | 18,2 | 18,8 | 18,8 | 19,0 | 18,7 | 18,2 | 21,1 |
| 18,9 | 19,6 | 18,7 | 18,6 | 19,2 | 18,2 | 19,8 | 19,9 | 18,8 | 18,9 |
Имеем объем выборки n=60 случайной величины х
Интервальный вариационный ряд распределения.
| 18,2 | 18,2 | 18,2 | 18,3 | 18,3 | 18,3 | 18,3 | 18,4 | 18,4 | 18,4 |
| 18,5 | 18,5 | 18,6 | 18,6 | 18,6 | 18,6 | 18,6 | 18,7 | 18,7 | 18,7 |
| 18,7 | 18,7 | 18,8 | 18,8 | 18,8 | 18,8 | 18,8 | 18,9 | 18,9 | 18,9 |
| 18,9 | 19,0 | 19,0 | 19,0 | 19,1 | 19,1 | 19,1 | 19,2 | 19,2 | 19,4 |
| 19,4 | 19,5 | 19,6 | 19,7 | 19,8 | 19,8 | 19,9 | 20,0 | 20,0 | 20,2 |
| 20,3 | 20,4 | 20,4 | 20,5 | 20,6 | 20,9 | 21,1 | 21,8 | 22,2 | 24,4 |
Определение: Расположение выбранных наблюдаемых значений случайной величины х в порядке возрастания называется ранжированием.
Расположим эти наблюдения не в порядке получения, а в порядке возрастания, получим следующий вариационный ряд.
Определение: Разность между max и min значениями выборки называется размахом выборки.
R= xmax-xmin =24,4-18,2=6,2 (1)
Диапазон наблюденных значений случайной величины х укладывается в интервал (18,0;25,0). Разбиваем интервал наблюденных значений случайной величины на 7 разрядов с шагом ∆= 1.
Численность отдельной группы сгруппированного ряда опытных данных называется выборочной частотой попадания.
Σmiх= n=60 (2)
Отношение выборочной частоты данной варианты к объему выборки называется относительной выборочной частотой.
Pxi=mix/n (3)
Все вычисления представлены в таблице:
| N | Li- L I+1 | mi-частота попадания | xi-середина интервала | относительная частотаPxi=mx/n | высота гистограммыhx= mx/∆•n | 
|
| 18,0...19,0 | 18,5 | 0,56 | 0,56 | 1,3 | ||
| 19,0…20,0 | 19,5 | 0,25 | 0,25 | 0,35 | ||
| 20,0…21,0 | 20,5 | 0,12 | 0,12 | 0,097 | ||
| 21,0…22,0 | 21,5 | 0,03 | 0,03 | 0,065 | ||
| 22,0…23,0 | 22,5 | 0,02 | 0,02 | 0,02 | ||
| 23,0…24,0 | 23,5 | 0,0087 | ||||
| 24,0…25,0 | 24,5 | 0,02 | 0,02 | 0,007 | ||
| Σmi= 60 | ΣPx=1 |
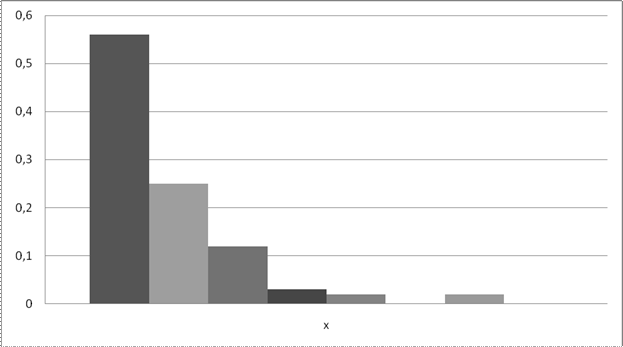
Гистограмма
Определение: Гистограмма - статистический аналог функции плотности непрерывной случайной величины х. По виду гистограммы можно выдвинуть гипотезу о расположении случайной величины х.
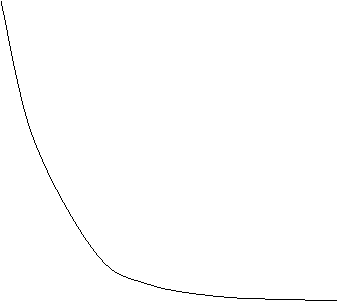
|
|
|
|
|
|
|
|
|
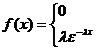
Оценки числовых характеристик и оценки параметров закона.
Определение: Оценка параметров генеральной совокупности, полученные на основе выборки называется статистической, если статистическая оценка характеризуется одним числом, то она называется точечной.
Выборочная средняя:
 =
=  (4)
(4)
 =1|60 (629 + 292,5 +143,5 +43+22,5+ 24,5) =19,25
=1|60 (629 + 292,5 +143,5 +43+22,5+ 24,5) =19,25
 =19,25-18,5=0,75
=19,25-18,5=0,75
Выборочная дисперсия:
 2=
2= 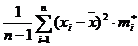 (5)
(5)
 2=1|59(19,1+0,9+10,9+10,1+10,6+27,6=1,35
2=1|59(19,1+0,9+10,9+10,1+10,6+27,6=1,35
Найдем оценки MX и DX
MX 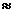 х=0,75
х=0,75
DX 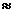 S2=0,473
S2=0,473
 =
= 