Математическое ожидание дискретной случайной величины
Произведение событий
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении ) этих событий. Например, если A —деталь годная, B - деталь окрашенная, то АВ —деталь годна и окрашена.
Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С — появление «герба» соответственно к первом, втором и третьем бросаниях монеты, то A,B,C — выпадение «герба» во всех трех испытаниях.
Задача
Вероятность того, что первый валик окажется конусным (событие А), Р (А)= 3/10. Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик— конусный, т. е. условная вероятность РА (В) = 7 / 9.
По теореме умножения, искомая вероятность Р (АВ) = Р (А) РА (В) = (3/10)-(7/9) = 7/30.Заметим, что, сохранив обозначения, легко найдем: Р (В)==7/10; РB (А) = 3 / 9, Р (В) РB (А)= 7/30
Билет № 19
1. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически. При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:
Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события X = х 1, X = х 2,..., X = хп образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице: p 1 +p 2 + …+pn= 1.
2. Формула полной вероятности
Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B 1 ,В 2 ,..., Вп, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
Р (A) = Р (B 1)  (А) + P (В 2) (А) + P (В 2)  (А) +... +Р (Вп) (А) +... +Р (Вп)  (А). (А).
Эту формулу называют «формулой полной вероятности».
Задача.
События А и В независимые, поэтому исходная вероятность будет читаться по формуле Р(АВ)=Р(А)*Р(В), Р(АВ)=0,7 *0,8 = 0,56
Ответ 0,56
Билет № 25
Математическое ожидание дискретной случайной величины
Пусть случайная величина X может принимать только значения х 1, х 2,..., хп, вероятности которых соответственно равны р 1, р 2,..., рп. Тогда математическое ожидание М (X) случайной величины X определяется равенством М (X) = х 1 р 1 + х 2 р 2 + … + xnpn
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
2. Формула полной вероятности
Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B 1 ,В 2 ,..., Вп, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
Р (A) = Р (B 1)  (А) + P (В 2) (А) + P (В 2)  (А) +... +Р (Вп) (А) +... +Р (Вп)  (А). (А).
Эту формулу называют «формулой полной вероятности».
3.Задача.
Вероятность появления «герба» в каждом бросании монеты р =1/2, следовательно, вероятность непоявления «герба» q = 1 — 1/2=1/2.
При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X таковы: x 1 = 2, x 2==1, x 3 = 0. Найдем вероятности этих возможных значений по формуле Бернулли:
Р 2(2) =  p 2 = (1 / 2)2 = 0, 25 ,Р 2(1) = p 2 = (1 / 2)2 = 0, 25 ,Р 2(1) =  pq= 2 * (1 / 2) * (1 / 2) = 0, 5, pq= 2 * (1 / 2) * (1 / 2) = 0, 5,
Р 2(0) =  q 2 = (1 / 2)2 = 0, 25. q 2 = (1 / 2)2 = 0, 25.
Напишем искомый закон распределения:
0,25 + 0,5 + 0,25=1.
| Билет № 9
1.. Вероятностный смысл математического ожидания: Математическое ожидание приблизительно равно среднему арифметическому наблюдаемых значений случайной величины
 где:mk– частота наблюдений, Wk– относительная частота.
2. Генеральная и выборочная совокупности
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов. Генеральной совокупностью называют совокупность объектов, из которых производится выборка
3.Задача.
Т.к надо найти вероятность события то задачу решаем по формуле вероятности P=m/n, где n- вероятность всех элементарных исходов
, т.к абонент мог набрать любую из 10 цифр то n = 10, так как нужна только одна правильная то m=1 Поставим значения в формулу вероятности и получим P=m/n=1/10 Ответ:вероятность того что набрана нужная цифра равна 1/10
Билет № 10
1. Числовые характеристики дискретных случайных величин
Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание.
2. Вероятность появления хотя бы одного из событий
А 1, А 2,..., Ап, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий где:mk– частота наблюдений, Wk– относительная частота.
2. Генеральная и выборочная совокупности
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов. Генеральной совокупностью называют совокупность объектов, из которых производится выборка
3.Задача.
Т.к надо найти вероятность события то задачу решаем по формуле вероятности P=m/n, где n- вероятность всех элементарных исходов
, т.к абонент мог набрать любую из 10 цифр то n = 10, так как нужна только одна правильная то m=1 Поставим значения в формулу вероятности и получим P=m/n=1/10 Ответ:вероятность того что набрана нужная цифра равна 1/10
Билет № 10
1. Числовые характеристики дискретных случайных величин
Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание.
2. Вероятность появления хотя бы одного из событий
А 1, А 2,..., Ап, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий  : P (A) = 1 — q 1 q 2 ... qn.
3.Задача.
Т.к надо найти вероятность события то задачу решаем по формуле вероятности P=m/n, где n- вероятность всех элементарных исходов
Обозначим через B событие – набраны две нужные цифры то
n= : P (A) = 1 — q 1 q 2 ... qn.
3.Задача.
Т.к надо найти вероятность события то задачу решаем по формуле вероятности P=m/n, где n- вероятность всех элементарных исходов
Обозначим через B событие – набраны две нужные цифры то
n= 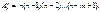 = А2/10=10*9=90 то n=90
Благоприятствует событию B лишь один исход, то m = 1. Подставим численные значения в формулу вероятности и получимP(B)=m/n= P (B)= 1/90.
Билет № 11
1.Целесообразность введения числовой характеристики рассеяния случайной величины
Зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью случайную величину не характеризует. По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики. Так, например, для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.
2. Вероятность гипотез. Формулы Бейеса
Пусть событие A может наступить при условии появления одного из несовместных событий B 1 ,В 2 ,..., Вп, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами
РА (Вi) = = А2/10=10*9=90 то n=90
Благоприятствует событию B лишь один исход, то m = 1. Подставим численные значения в формулу вероятности и получимP(B)=m/n= P (B)= 1/90.
Билет № 11
1.Целесообразность введения числовой характеристики рассеяния случайной величины
Зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью случайную величину не характеризует. По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики. Так, например, для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.
2. Вероятность гипотез. Формулы Бейеса
Пусть событие A может наступить при условии появления одного из несовместных событий B 1 ,В 2 ,..., Вп, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами
РА (Вi) =  Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
3.Задача
Т.к надо найти вероятность события то задачу решаем по формуле геометрической вероятности P=Пм/Пб, где Пб- площадь круга = ПR^2, Пм – площадь вписоного квадрата, её находим исходя из теоремы Пифагора R^2+R^2 =a^2=2R^2-Площадь квадрата. Подставляем значения в формулу получаем P=Пм/Пб=2R^2/ ПR^2=2/П
Билет № 20
1. Дисперсия числа появлений события в независимых испытаниях
Дисперсия числа появлений события А в п независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:D (X) = npq.
2. Теорема умножения вероятностей
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р (АВ) = Р (А) РА (В).
3. Задача
Вероятность события появления герба при одном бросании 2 монет, независимые решаются по формуле умножения независимых вероятностей Р (АВ) = Р (А) Р (В).
, найдем Р (А), n=2, m= 1, решаем по формуле вероятности P(А)=m/n=1/2=0,5 P(B)=0,5.Подставим значения в формулу умножения независимых вероятностей
Р (АВ) = 0,5*0,5=0,25 Ответ 0.25
Билет № 21
1. Дискретные и непрерывные случайные величины
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
2. Задачи математической статистики
Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики - разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:
а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;
б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов
3 Задача
События независимые поэтому вероятность будем искать по формуле умножения независимых вероятностей Р (АВ) = Р (А) Р (В) ., найдем Р (А), n=2, m= 1, решаем по формуле вероятности P(А)=m/n=1/2=0,5, найдем P(B) где m =1, n=6 P(B) =1/6 Поставим значения в формулу умножения независимых вероятностей Р (АВ) = Р (А) Р (В) = 1/2*1/6 = 1/12
Билет № 22
1. Свойства функции распределения
Свойство 1. Значения функции распределения принадлежат отрезку [О, 1]: 0≤ F (х) ≤1.
Свойство 2. F (х)— неубывающая функция,т. е.F (x 2) > F (х 1), если х 2> х 1.
Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а, b), то: 1) F (x) = 0 при х ≤ а; 2) F (x) = 1 при х > b.
2.Условная вероятность
.Если при вычислении вероятности события никаких других ограничений, кроме условий S, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной.
Условной вероятностью РА (В)называют вероятность события В, вычисленную в предположении, что событие А уже наступило
3.Задача
Найдем математическое ожидание X: М (Х) = 1 • 0, 2 + 2 • 0, 8 = 1, 8.
Найдем возможные значения отклонения, для чего из возможных значений X вычтем математическое ожидание М (Х): 1 — 1,8 = —0,8; 2—1,8 = 0,2.
Напишем закон распределения отклонения:
Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
3.Задача
Т.к надо найти вероятность события то задачу решаем по формуле геометрической вероятности P=Пм/Пб, где Пб- площадь круга = ПR^2, Пм – площадь вписоного квадрата, её находим исходя из теоремы Пифагора R^2+R^2 =a^2=2R^2-Площадь квадрата. Подставляем значения в формулу получаем P=Пм/Пб=2R^2/ ПR^2=2/П
Билет № 20
1. Дисперсия числа появлений события в независимых испытаниях
Дисперсия числа появлений события А в п независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:D (X) = npq.
2. Теорема умножения вероятностей
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р (АВ) = Р (А) РА (В).
3. Задача
Вероятность события появления герба при одном бросании 2 монет, независимые решаются по формуле умножения независимых вероятностей Р (АВ) = Р (А) Р (В).
, найдем Р (А), n=2, m= 1, решаем по формуле вероятности P(А)=m/n=1/2=0,5 P(B)=0,5.Подставим значения в формулу умножения независимых вероятностей
Р (АВ) = 0,5*0,5=0,25 Ответ 0.25
Билет № 21
1. Дискретные и непрерывные случайные величины
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
2. Задачи математической статистики
Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики - разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:
а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;
б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов
3 Задача
События независимые поэтому вероятность будем искать по формуле умножения независимых вероятностей Р (АВ) = Р (А) Р (В) ., найдем Р (А), n=2, m= 1, решаем по формуле вероятности P(А)=m/n=1/2=0,5, найдем P(B) где m =1, n=6 P(B) =1/6 Поставим значения в формулу умножения независимых вероятностей Р (АВ) = Р (А) Р (В) = 1/2*1/6 = 1/12
Билет № 22
1. Свойства функции распределения
Свойство 1. Значения функции распределения принадлежат отрезку [О, 1]: 0≤ F (х) ≤1.
Свойство 2. F (х)— неубывающая функция,т. е.F (x 2) > F (х 1), если х 2> х 1.
Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а, b), то: 1) F (x) = 0 при х ≤ а; 2) F (x) = 1 при х > b.
2.Условная вероятность
.Если при вычислении вероятности события никаких других ограничений, кроме условий S, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной.
Условной вероятностью РА (В)называют вероятность события В, вычисленную в предположении, что событие А уже наступило
3.Задача
Найдем математическое ожидание X: М (Х) = 1 • 0, 2 + 2 • 0, 8 = 1, 8.
Найдем возможные значения отклонения, для чего из возможных значений X вычтем математическое ожидание М (Х): 1 — 1,8 = —0,8; 2—1,8 = 0,2.
Напишем закон распределения отклонения:
| X-M (X)
| - 0, 8
| 0, 2
| | p
| 0, 2
| 0, 8
| Найдем математическое ожидание отклонения:
М [ Х — М (Х)] = (— 0, 8) • 0, 2 + 0, 2 • 0, 8 = 0.
| Билет № 12
1. Полигон и гистограмма
Полигоном частот называют ломаную, отрезки которой соединяют точки (x 1, n 1), (х 2; n 2),..., (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им частоты nj. Точки (xi; пi)соединяют отрезками прямых и получают полигон частот.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению ni/h (плотность частоты).Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni/h.
2.Вероятность попадания в заданный интервал нормальной случайной величины
Уже известно, что если случайная величина X задана плотностью распределения f (х), то вероятность того, что X примет значение, принадлежащее интервалу (a,b), такова:
P (a< X< b) =  Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (a,b), равна
P (a< X< b) =
Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (a,b), равна
P (a< X< b) =  Преобразуем эту формулу,окончательно получим
Преобразуем эту формулу,окончательно получим
 3.Задача.
Появление цветного шара означает появление либо красного либо синего шара, пусть вероятность появления красного шара это события А тогда, P(A)= m/n, где m=10 n =30 P(A)=1/3 вероятность появления синего шара P(B) = m/n где m = 5,n =30, где P(B) = 1/6, событие А и B несовместные поэтому можно применить теорему сложения P(A)+P(B)=P(A+B)= 1//3+1/6=1/2
Ответ: вероятность появления цветного шара равна ½
Билет № 13
1. Классическое определение вероятности
Вероятностью события A называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события A определяется формулой P (A) = m/n, где m – число элементарных исходов, благоприятствующих A; n – число всех возможных элементарных исходов испытания. Свойство 1. Вероятность достоверного события равна единице. P (A) = m / n = n / n = 1.
Свойство 2. Вероятность невозможного события равна нулю
P (A) = m / n = 0/ n = 0.Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. 0≤ P (A) ≤1.
2. Закон равномерного распределения вероятностей
Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются, например, законы равномерного, нормального и показательного распределений Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
3.Задача.
События А,Б,С образуют полную группу, поэтому сумма вероятностей этих событий равна 1.следовательно 0,7+ 0,2+р =1
Отсюда вероятность р= 1 – 0,9 = 0,1 Ответ: 0,1
Билет № 23
1,Свойства плотности распределения Вероятностный смысл плотности распределения
Свойство 1. Плотность распределения — неотрицательная функция: f (x) > 0.
Свойство 2. Несобственный интеграл от плотности распределения в пределах от -
3.Задача.
Появление цветного шара означает появление либо красного либо синего шара, пусть вероятность появления красного шара это события А тогда, P(A)= m/n, где m=10 n =30 P(A)=1/3 вероятность появления синего шара P(B) = m/n где m = 5,n =30, где P(B) = 1/6, событие А и B несовместные поэтому можно применить теорему сложения P(A)+P(B)=P(A+B)= 1//3+1/6=1/2
Ответ: вероятность появления цветного шара равна ½
Билет № 13
1. Классическое определение вероятности
Вероятностью события A называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события A определяется формулой P (A) = m/n, где m – число элементарных исходов, благоприятствующих A; n – число всех возможных элементарных исходов испытания. Свойство 1. Вероятность достоверного события равна единице. P (A) = m / n = n / n = 1.
Свойство 2. Вероятность невозможного события равна нулю
P (A) = m / n = 0/ n = 0.Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. 0≤ P (A) ≤1.
2. Закон равномерного распределения вероятностей
Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются, например, законы равномерного, нормального и показательного распределений Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
3.Задача.
События А,Б,С образуют полную группу, поэтому сумма вероятностей этих событий равна 1.следовательно 0,7+ 0,2+р =1
Отсюда вероятность р= 1 – 0,9 = 0,1 Ответ: 0,1
Билет № 23
1,Свойства плотности распределения Вероятностный смысл плотности распределения
Свойство 1. Плотность распределения — неотрицательная функция: f (x) > 0.
Свойство 2. Несобственный интеграл от плотности распределения в пределах от -  до до  равен единице: равен единице: 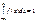 Пусть F (х)—функция распределения непрерывной случайной величины X. По определению плотности распределения, f (х)= F' (х), Так как F' (x) = f (x)и dx=
Пусть F (х)—функция распределения непрерывной случайной величины X. По определению плотности распределения, f (х)= F' (х), Так как F' (x) = f (x)и dx=  х, то F (х+ х, то F (х+  х) — F (х) х) — F (х)  f (x) f (x)  х. Вероятностный смысл этого равенства таков: вероятность того, что случайная величина примет значение, принадлежащее интервалу (х, х + х. Вероятностный смысл этого равенства таков: вероятность того, что случайная величина примет значение, принадлежащее интервалу (х, х +  х), приближенно равна (с точностью до бесконечно малых высшего порядка относительно х), приближенно равна (с точностью до бесконечно малых высшего порядка относительно  х)произведению плотности вероятности в точке х на длину интервала х)произведению плотности вероятности в точке х на длину интервала  х.
2. Числовые характеристики непрерывных случайных величин
Математическим ожиданием непрерывной случайной величины- X, Возможные значения которой принадлежат отрезку [ a,b ], называют определенный интеграл
M (X) = х.
2. Числовые характеристики непрерывных случайных величин
Математическим ожиданием непрерывной случайной величины- X, Возможные значения которой принадлежат отрезку [ a,b ], называют определенный интеграл
M (X) =  Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Если возможные значения X принадлежат отрезку[ a,b ], то
D (X) =
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Если возможные значения X принадлежат отрезку[ a,b ], то
D (X) =  Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенствомs(X) =
Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенствомs(X) =  .
3.Задача
M(x)=0,3+1+1=2,3 (x-M(x))^ (x1-M(x))^2 (x2-M(x))^2 (X3-M(x))^2
X1=1,69 x2=0,09 x3= 7,29 D(x)=1,69*0,3+0,09*0,5+7,29*0,2=2,01
Билет № 24
1.Вероятность попадания непрерывной случайной велечены в заданный интервал
Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b: Р (а<Х<b) = .
3.Задача
M(x)=0,3+1+1=2,3 (x-M(x))^ (x1-M(x))^2 (x2-M(x))^2 (X3-M(x))^2
X1=1,69 x2=0,09 x3= 7,29 D(x)=1,69*0,3+0,09*0,5+7,29*0,2=2,01
Билет № 24
1.Вероятность попадания непрерывной случайной велечены в заданный интервал
Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b: Р (а<Х<b) =  2.Теорема сложения вероятностей совместных событий
Вероятность появления хотя бы одного из двухсовместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р (А + В) = Р (А) + Р (В) — Р (АВ).
3.Задача
M(x)=x1p1+x2p2=x3p3+x4p4=0,04+0,4+1,5+5=6,94
(x-M(x))^ (x1-M(x))^2 (x2-M(x))^2 (x3-M(x))^2 (x4-M(x))^2
x1=(0,1-6,94)^2=46,7856 x2=(2-6,94)^2=24,4036 x3= (10-6,94)^2=9,3636 x4 = (20-6,94)^2=170,5636 D(x)= 46,7856*0,4+24,4036*0,2+9,3636*0.15+170,5636*0,35=18,71424+4,88072+1,40454+42,6409= 67,6404 Ответ D(x)= 67,6404
2.Теорема сложения вероятностей совместных событий
Вероятность появления хотя бы одного из двухсовместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р (А + В) = Р (А) + Р (В) — Р (АВ).
3.Задача
M(x)=x1p1+x2p2=x3p3+x4p4=0,04+0,4+1,5+5=6,94
(x-M(x))^ (x1-M(x))^2 (x2-M(x))^2 (x3-M(x))^2 (x4-M(x))^2
x1=(0,1-6,94)^2=46,7856 x2=(2-6,94)^2=24,4036 x3= (10-6,94)^2=9,3636 x4 = (20-6,94)^2=170,5636 D(x)= 46,7856*0,4+24,4036*0,2+9,3636*0.15+170,5636*0,35=18,71424+4,88072+1,40454+42,6409= 67,6404 Ответ D(x)= 67,6404
|
 (А) + P (В 2)
(А) + P (В 2)  (А) +... +Р (Вп)
(А) +... +Р (Вп)  (А).
(А). (А) + P (В 2)
(А) + P (В 2)  (А) +... +Р (Вп)
(А) +... +Р (Вп)  (А).
(А). p 2 = (1 / 2)2 = 0, 25 ,Р 2(1) =
p 2 = (1 / 2)2 = 0, 25 ,Р 2(1) =  pq= 2 * (1 / 2) * (1 / 2) = 0, 5,
pq= 2 * (1 / 2) * (1 / 2) = 0, 5, q 2 = (1 / 2)2 = 0, 25.
q 2 = (1 / 2)2 = 0, 25. где:mk– частота наблюдений, Wk– относительная частота.
2. Генеральная и выборочная совокупности
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов. Генеральной совокупностью называют совокупность объектов, из которых производится выборка
3.Задача.
Т.к надо найти вероятность события то задачу решаем по формуле вероятности P=m/n, где n- вероятность всех элементарных исходов
, т.к абонент мог набрать любую из 10 цифр то n = 10, так как нужна только одна правильная то m=1 Поставим значения в формулу вероятности и получим P=m/n=1/10 Ответ:вероятность того что набрана нужная цифра равна 1/10
Билет № 10
1. Числовые характеристики дискретных случайных величин
Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание.
2. Вероятность появления хотя бы одного из событий
А 1, А 2,..., Ап, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
где:mk– частота наблюдений, Wk– относительная частота.
2. Генеральная и выборочная совокупности
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов. Генеральной совокупностью называют совокупность объектов, из которых производится выборка
3.Задача.
Т.к надо найти вероятность события то задачу решаем по формуле вероятности P=m/n, где n- вероятность всех элементарных исходов
, т.к абонент мог набрать любую из 10 цифр то n = 10, так как нужна только одна правильная то m=1 Поставим значения в формулу вероятности и получим P=m/n=1/10 Ответ:вероятность того что набрана нужная цифра равна 1/10
Билет № 10
1. Числовые характеристики дискретных случайных величин
Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание.
2. Вероятность появления хотя бы одного из событий
А 1, А 2,..., Ап, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий  : P (A) = 1 — q 1 q 2 ... qn.
3.Задача.
Т.к надо найти вероятность события то задачу решаем по формуле вероятности P=m/n, где n- вероятность всех элементарных исходов
Обозначим через B событие – набраны две нужные цифры то
n=
: P (A) = 1 — q 1 q 2 ... qn.
3.Задача.
Т.к надо найти вероятность события то задачу решаем по формуле вероятности P=m/n, где n- вероятность всех элементарных исходов
Обозначим через B событие – набраны две нужные цифры то
n= 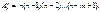 = А2/10=10*9=90 то n=90
Благоприятствует событию B лишь один исход, то m = 1. Подставим численные значения в формулу вероятности и получимP(B)=m/n= P (B)= 1/90.
Билет № 11
1.Целесообразность введения числовой характеристики рассеяния случайной величины
Зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью случайную величину не характеризует. По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики. Так, например, для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.
2. Вероятность гипотез. Формулы Бейеса
Пусть событие A может наступить при условии появления одного из несовместных событий B 1 ,В 2 ,..., Вп, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами
РА (Вi) =
= А2/10=10*9=90 то n=90
Благоприятствует событию B лишь один исход, то m = 1. Подставим численные значения в формулу вероятности и получимP(B)=m/n= P (B)= 1/90.
Билет № 11
1.Целесообразность введения числовой характеристики рассеяния случайной величины
Зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью случайную величину не характеризует. По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики. Так, например, для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.
2. Вероятность гипотез. Формулы Бейеса
Пусть событие A может наступить при условии появления одного из несовместных событий B 1 ,В 2 ,..., Вп, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами
РА (Вi) =  Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
3.Задача
Т.к надо найти вероятность события то задачу решаем по формуле геометрической вероятности P=Пм/Пб, где Пб- площадь круга = ПR^2, Пм – площадь вписоного квадрата, её находим исходя из теоремы Пифагора R^2+R^2 =a^2=2R^2-Площадь квадрата. Подставляем значения в формулу получаем P=Пм/Пб=2R^2/ ПR^2=2/П
Билет № 20
1. Дисперсия числа появлений события в независимых испытаниях
Дисперсия числа появлений события А в п независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:D (X) = npq.
2. Теорема умножения вероятностей
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р (АВ) = Р (А) РА (В).
3. Задача
Вероятность события появления герба при одном бросании 2 монет, независимые решаются по формуле умножения независимых вероятностей Р (АВ) = Р (А) Р (В).
, найдем Р (А), n=2, m= 1, решаем по формуле вероятности P(А)=m/n=1/2=0,5 P(B)=0,5.Подставим значения в формулу умножения независимых вероятностей
Р (АВ) = 0,5*0,5=0,25 Ответ 0.25
Билет № 21
1. Дискретные и непрерывные случайные величины
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
2. Задачи математической статистики
Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики - разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:
а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;
б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов
3 Задача
События независимые поэтому вероятность будем искать по формуле умножения независимых вероятностей Р (АВ) = Р (А) Р (В) ., найдем Р (А), n=2, m= 1, решаем по формуле вероятности P(А)=m/n=1/2=0,5, найдем P(B) где m =1, n=6 P(B) =1/6 Поставим значения в формулу умножения независимых вероятностей Р (АВ) = Р (А) Р (В) = 1/2*1/6 = 1/12
Билет № 22
1. Свойства функции распределения
Свойство 1. Значения функции распределения принадлежат отрезку [О, 1]: 0≤ F (х) ≤1.
Свойство 2. F (х)— неубывающая функция,т. е.F (x 2) > F (х 1), если х 2> х 1.
Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а, b), то: 1) F (x) = 0 при х ≤ а; 2) F (x) = 1 при х > b.
2.Условная вероятность
.Если при вычислении вероятности события никаких других ограничений, кроме условий S, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной.
Условной вероятностью РА (В)называют вероятность события В, вычисленную в предположении, что событие А уже наступило
3.Задача
Найдем математическое ожидание X: М (Х) = 1 • 0, 2 + 2 • 0, 8 = 1, 8.
Найдем возможные значения отклонения, для чего из возможных значений X вычтем математическое ожидание М (Х): 1 — 1,8 = —0,8; 2—1,8 = 0,2.
Напишем закон распределения отклонения:
Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
3.Задача
Т.к надо найти вероятность события то задачу решаем по формуле геометрической вероятности P=Пм/Пб, где Пб- площадь круга = ПR^2, Пм – площадь вписоного квадрата, её находим исходя из теоремы Пифагора R^2+R^2 =a^2=2R^2-Площадь квадрата. Подставляем значения в формулу получаем P=Пм/Пб=2R^2/ ПR^2=2/П
Билет № 20
1. Дисперсия числа появлений события в независимых испытаниях
Дисперсия числа появлений события А в п независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:D (X) = npq.
2. Теорема умножения вероятностей
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р (АВ) = Р (А) РА (В).
3. Задача
Вероятность события появления герба при одном бросании 2 монет, независимые решаются по формуле умножения независимых вероятностей Р (АВ) = Р (А) Р (В).
, найдем Р (А), n=2, m= 1, решаем по формуле вероятности P(А)=m/n=1/2=0,5 P(B)=0,5.Подставим значения в формулу умножения независимых вероятностей
Р (АВ) = 0,5*0,5=0,25 Ответ 0.25
Билет № 21
1. Дискретные и непрерывные случайные величины
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
2. Задачи математической статистики
Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики - разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:
а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;
б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов
3 Задача
События независимые поэтому вероятность будем искать по формуле умножения независимых вероятностей Р (АВ) = Р (А) Р (В) ., найдем Р (А), n=2, m= 1, решаем по формуле вероятности P(А)=m/n=1/2=0,5, найдем P(B) где m =1, n=6 P(B) =1/6 Поставим значения в формулу умножения независимых вероятностей Р (АВ) = Р (А) Р (В) = 1/2*1/6 = 1/12
Билет № 22
1. Свойства функции распределения
Свойство 1. Значения функции распределения принадлежат отрезку [О, 1]: 0≤ F (х) ≤1.
Свойство 2. F (х)— неубывающая функция,т. е.F (x 2) > F (х 1), если х 2> х 1.
Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а, b), то: 1) F (x) = 0 при х ≤ а; 2) F (x) = 1 при х > b.
2.Условная вероятность
.Если при вычислении вероятности события никаких других ограничений, кроме условий S, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной.
Условной вероятностью РА (В)называют вероятность события В, вычисленную в предположении, что событие А уже наступило
3.Задача
Найдем математическое ожидание X: М (Х) = 1 • 0, 2 + 2 • 0, 8 = 1, 8.
Найдем возможные значения отклонения, для чего из возможных значений X вычтем математическое ожидание М (Х): 1 — 1,8 = —0,8; 2—1,8 = 0,2.
Напишем закон распределения отклонения:
 Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (a,b), равна
P (a< X< b) =
Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (a,b), равна
P (a< X< b) =  Преобразуем эту формулу,окончательно получим
Преобразуем эту формулу,окончательно получим
 3.Задача.
Появление цветного шара означает появление либо красного либо синего шара, пусть вероятность появления красного шара это события А тогда, P(A)= m/n, где m=10 n =30 P(A)=1/3 вероятность появления синего шара P(B) = m/n где m = 5,n =30, где P(B) = 1/6, событие А и B несовместные поэтому можно применить теорему сложения P(A)+P(B)=P(A+B)= 1//3+1/6=1/2
Ответ: вероятность появления цветного шара равна ½
Билет № 13
1. Классическое определение вероятности
Вероятностью события A называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события A определяется формулой P (A) = m/n, где m – число элементарных исходов, благоприятствующих A; n – число всех возможных элементарных исходов испытания. Свойство 1. Вероятность достоверного события равна единице. P (A) = m / n = n / n = 1.
Свойство 2. Вероятность невозможного события равна нулю
P (A) = m / n = 0/ n = 0.Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. 0≤ P (A) ≤1.
2. Закон равномерного распределения вероятностей
Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются, например, законы равномерного, нормального и показательного распределений Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
3.Задача.
События А,Б,С образуют полную группу, поэтому сумма вероятностей этих событий равна 1.следовательно 0,7+ 0,2+р =1
Отсюда вероятность р= 1 – 0,9 = 0,1 Ответ: 0,1
Билет № 23
1,Свойства плотности распределения Вероятностный смысл плотности распределения
Свойство 1. Плотность распределения — неотрицательная функция: f (x) > 0.
Свойство 2. Несобственный интеграл от плотности распределения в пределах от -
3.Задача.
Появление цветного шара означает появление либо красного либо синего шара, пусть вероятность появления красного шара это события А тогда, P(A)= m/n, где m=10 n =30 P(A)=1/3 вероятность появления синего шара P(B) = m/n где m = 5,n =30, где P(B) = 1/6, событие А и B несовместные поэтому можно применить теорему сложения P(A)+P(B)=P(A+B)= 1//3+1/6=1/2
Ответ: вероятность появления цветного шара равна ½
Билет № 13
1. Классическое определение вероятности
Вероятностью события A называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события A определяется формулой P (A) = m/n, где m – число элементарных исходов, благоприятствующих A; n – число всех возможных элементарных исходов испытания. Свойство 1. Вероятность достоверного события равна единице. P (A) = m / n = n / n = 1.
Свойство 2. Вероятность невозможного события равна нулю
P (A) = m / n = 0/ n = 0.Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. 0≤ P (A) ≤1.
2. Закон равномерного распределения вероятностей
Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются, например, законы равномерного, нормального и показательного распределений Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
3.Задача.
События А,Б,С образуют полную группу, поэтому сумма вероятностей этих событий равна 1.следовательно 0,7+ 0,2+р =1
Отсюда вероятность р= 1 – 0,9 = 0,1 Ответ: 0,1
Билет № 23
1,Свойства плотности распределения Вероятностный смысл плотности распределения
Свойство 1. Плотность распределения — неотрицательная функция: f (x) > 0.
Свойство 2. Несобственный интеграл от плотности распределения в пределах от -  до
до 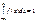 Пусть F (х)—функция распределения непрерывной случайной величины X. По определению плотности распределения, f (х)= F' (х), Так как F' (x) = f (x)и dx=
Пусть F (х)—функция распределения непрерывной случайной величины X. По определению плотности распределения, f (х)= F' (х), Так как F' (x) = f (x)и dx=  х, то F (х+
х, то F (х+  х) — F (х)
х) — F (х)  f (x)
f (x)  х), приближенно равна (с точностью до бесконечно малых высшего порядка относительно
х), приближенно равна (с точностью до бесконечно малых высшего порядка относительно  Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Если возможные значения X принадлежат отрезку[ a,b ], то
D (X) =
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Если возможные значения X принадлежат отрезку[ a,b ], то
D (X) =  Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенствомs(X) =
Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенствомs(X) =  .
3.Задача
M(x)=0,3+1+1=2,3 (x-M(x))^ (x1-M(x))^2 (x2-M(x))^2 (X3-M(x))^2
X1=1,69 x2=0,09 x3= 7,29 D(x)=1,69*0,3+0,09*0,5+7,29*0,2=2,01
Билет № 24
1.Вероятность попадания непрерывной случайной велечены в заданный интервал
Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b: Р (а<Х<b) =
.
3.Задача
M(x)=0,3+1+1=2,3 (x-M(x))^ (x1-M(x))^2 (x2-M(x))^2 (X3-M(x))^2
X1=1,69 x2=0,09 x3= 7,29 D(x)=1,69*0,3+0,09*0,5+7,29*0,2=2,01
Билет № 24
1.Вероятность попадания непрерывной случайной велечены в заданный интервал
Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b: Р (а<Х<b) =  2.Теорема сложения вероятностей совместных событий
Вероятность появления хотя бы одного из двухсовместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р (А + В) = Р (А) + Р (В) — Р (АВ).
3.Задача
M(x)=x1p1+x2p2=x3p3+x4p4=0,04+0,4+1,5+5=6,94
(x-M(x))^ (x1-M(x))^2 (x2-M(x))^2 (x3-M(x))^2 (x4-M(x))^2
x1=(0,1-6,94)^2=46,7856 x2=(2-6,94)^2=24,4036 x3= (10-6,94)^2=9,3636 x4 = (20-6,94)^2=170,5636 D(x)= 46,7856*0,4+24,4036*0,2+9,3636*0.15+170,5636*0,35=18,71424+4,88072+1,40454+42,6409= 67,6404 Ответ D(x)= 67,6404
2.Теорема сложения вероятностей совместных событий
Вероятность появления хотя бы одного из двухсовместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р (А + В) = Р (А) + Р (В) — Р (АВ).
3.Задача
M(x)=x1p1+x2p2=x3p3+x4p4=0,04+0,4+1,5+5=6,94
(x-M(x))^ (x1-M(x))^2 (x2-M(x))^2 (x3-M(x))^2 (x4-M(x))^2
x1=(0,1-6,94)^2=46,7856 x2=(2-6,94)^2=24,4036 x3= (10-6,94)^2=9,3636 x4 = (20-6,94)^2=170,5636 D(x)= 46,7856*0,4+24,4036*0,2+9,3636*0.15+170,5636*0,35=18,71424+4,88072+1,40454+42,6409= 67,6404 Ответ D(x)= 67,6404