Мы заподозрили, что безуспешность попыток разгадать секрет «аномалии Эксплорера» обусловлена неправильной постановкой задачи. Ведь задача ставилась так: объяснить, почему вместо ожидаемой эллиптической орбиты получилась другая эллиптическая орбита. Но действительно ли получившаяся орбита была эллиптической? Ведь Эксплорер-1, имевший вид трубы – головного отсека с аппаратурой и пустой оболочки двигателя четвёртой ступени – продолжал быстрое вращение вокруг своей продольной оси, сохраняя в полёте ориентацию этой оси в пространстве. Не может ли оказаться, что такие вращающиеся болванки летают отнюдь не по кеплеровым орбитам? и что их траектории могут даже не лежать в одной плоскости? Может, Эксплорер-1 вовсе не забирался на увеличенную высоту перигея, а где-то на орбите «вильнул в сторону» и удлинил свой путь? Казалось бы, что силам, необходимым для подобных боковых манёвров, просто неоткуда взяться – если подходить к вопросу в рамках ортодоксальных воззрений. Но мы усматриваем причину для бокового сноса Эксплорера-1.
Рассмотрим случай свободного диска, который быстро вращается в вертикальной плоскости, и его горизонтальная и вертикальная скорости близки к нулю. Если бы диск не вращался, то тяготение сообщало бы одно и то же ускорение свободного падения каждому элементу объёма диска, и он был бы не деформирован. При вращении же диска возникают деформации – причём, не только центрально-симметричные деформации растяжения из-за центробежных сил в диске. Заметим: когда элемент объёма диска, который вращается на радиусе r, переходит из своего верхнего положения в нижнее, он должен испытывать гравитационный прирост линейной скорости вращения, соответствующий гравитационному изменению энергии mg 2 r, где m - масса элемента объёма, g - ускорение свободного падения. С другой же стороны вращающегося диска – при подъёме элемента объёма из нижнего положения в верхнее – должно происходить гравитационное уменьшение линейной скорости вращения. Поскольку эти гравитационные эффекты в итоге не сказываются на угловой скорости вращения диска, то уместен вопрос: каким образом эти эффекты «отрабатываются»? Мы полагаем, что они «отрабатываются» через механические деформации диска, которые несколько снижают линейную скорость вращательного движения вниз и, наоборот, повышают линейную скорость вращательного движения вверх. При постоянной угловой скорости вращения, это делается через изменения радиусов вращения: диск оказывается «поджат» со стороны вращательного движения вниз и, наоборот, «раздут» со стороны вращательного движения вверх. Таким образом, вращающийся диск должен иметь деформацию сжатия-растяжения в горизонтальном направлении.
Такая деформация в свободном теле должна являться, на наш взгляд, источником безопорной горизонтальной тяги. Действительно, нам известно два основных способа силового воздействия на тело: либо через временную деформацию, т.е. через градиент частот в теле (как это делает, например, тяготение [8]), либо через пространственную деформацию растяжения или сжатия (как это делают, например, механические силы – тянущие или толкающие). Оба этих способа порождают в теле градиент собственных энергий у частиц вещества – а градиент энергий, по определению, означает силовое воздействие: F =-(dE/d r). Тяготение порождает градиент энергий, формируя перепад энергий у частиц, а механическое воздействие порождает градиент энергий, формируя перепад расстояний между частицами. Когда тело, на которое действует тяготение, «не падает» благодаря опоре или подвесу – это значит, что в теле силовое действие временных деформаций уравновешено силовым действием пространственных деформаций. При этом, типичное относительное укорочение или удлинение тела вдоль вертикали, при g =9.8 м/с2, имеет порядок 10-6. В случае свободного вращающегося диска, силовое действие вышеописанной деформации сжатия-растяжения не уравновешено, поэтому диск должен испытывать тягу в ту сторону, с которой имеется деформация растяжения, т.е. где происходит вращательное движение вверх.
Строгий расчёт ускорения этой тяги, через поле деформаций сжатия-растяжения, представляет собой весьма сложную задачу; мы ограничимся упрощённым подходом. При постоянной угловой скорости w вращения диска, картина деформаций, дающих боковой снос, не эволюционирует, поэтому ускорение бокового сноса при этом должно быть постоянно. По вышеописанной логике появления этих деформаций, для элемента объёма, вращающегося на радиусе r, приращение линейной скорости wD r вращательного движения вверх или вниз должно быть пропорционально гравитационному приращению этой скорости, т.е.
. (1)
На основе (1), для ускорения бокового сноса a S диска с радиусом r можно записать:
, (2)
где безразмерные множители Q и x имеют следующий смысл. 
- геометрический фактор, отражающий средневзвешенную сумму вкладов в a S от элементов объёма диска, которые вращаются по разлным радиусам; для однородного диска или цилиндра Q =0.8. Фактор же x, который много меньше единицы, отражает эффективность действия боковых деформаций во вращающемся диске – она, например, значительно меньше эффективности действия деформаций, которые создаются при механическом воздействии в торец стержня, из-за очевидных различий в геометрии этих двух случаев. Фактор x, по-видимому, уменьшается при увеличении как радиуса диска, так и угловой скорости его вращения. Подчеркнём, что в энергию бокового движения вращающегося свободного диска превращается не энергия его боковых деформаций и, тем более, не энергия его вращения. Боковые деформации являются в данном случае чисто геометрическим эффектом, обеспечивающим безопорную тягу. Энергия же бокового движения должна расти за счёт убыли собственных энергий частиц вещества диска – согласно принципу автономных превращений энергии [9].
Заметим: в описанном выше примере, лишь тяготение оказывает силовое воздействие на диск вдоль вертикали. Полагают, что и для полёта спутника Земли по стационарной орбите достаточно, в принципе, только центростремительной силы, т.е. силы тяготения. Эти представления, на наш взгляд, некорректны. Если в однородном поле тяготения пробное тело движется по эквипотенциальной поверхности – по горизонтальной плоскости – т.е., «не падает», то это означает, что действие тяготения уравновешено какой-то другой силой. Аналогично, при движении по круговой орбите тело тоже движется по эквипотенциальной поверхности, и это означает, что действие тяготения тоже чем-то уравновешено. Мы полагаем, что оно уравновешено центробежной силой – которая, как и сила тяготения, имеет частотно-градиентную природу [10]. При этом величина центробежного ускорения есть квадрат тангенциальной компоненты орбитальной скорости (т.е. компоненты, ортогональной радиус-вектору), делённый на длину радиус-вектора. При движении спутника по круговой орбите, сила тяготения и центробежная сила равны друг другу. При движении по эллиптической орбите, на перигейном участке центробежная сила больше, чем сила тяготения, а на апогейном участке – ситуация противоположная. Учитывая центробежную силу при движении спутника, мы не только получаем хорошо известные кеплеровы орбиты, но и делаем нетривиальные предсказания, которые подтверждаются на опыте [11].
Проиллюстрируем поведение центробежной силы, в сравнении с силой тяготения, при полёте по расчётной орбите Эксплорера-1. Как отмечалось выше, центробежное ускорение a CB есть
a CB=(V orb×cos b)2/ R, (3)
где V orb - модуль орбитальной скорости, b - угол между вектором орбитальной скорости и плоскостью, ортогональной к радиус-вектору, R - длина радиус-вектора. Выражения для этих величин имеют вид [12]:
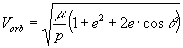, (4)
, (5)
, (6)
где m =3.987×1014 м3/с2 – гравитационный параметр Земли, p и e - фокальный параметр и эксцентриситет орбиты (для расчётной орбиты Эксплорера-1 p =7208 км, e =0.0929), q - угол положения радиус-вектора, отсчитываемый от направления на перигей. При малом эксцентриситете орбиты, можно без заметной потери точности дальнейших расчётов считать угловую скорость вращения радиус-вектора постоянной, т.е. зависимость угла q от времени считать линейной: q (t)=2p t / T, где T - период обращения. На основе известного соотношения [4] между периодом обращения по эллиптической орбите и длиной её большой полуоси A,
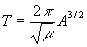, (7)
для периода обращения по расчётной орбите Эксплорера-1, при A =7271 км, получаем T =6169 секунд. Для этой орбиты, на Рис.1 показаны гравитационное ускорение (aG = m / R 2) и центробежное ускорение a CB, в единицах м/c2, как функции времени (точки 0 и 6169 с соответствуют перигею).
Рис.1
По логике вышеизложенного, для расчёта ускорения бокового сноса вращающегося спутника следует в выражении (2), вместо гравитационного ускорения, использовать модуль разности D a гравитационного и центробежного ускорений – в проекции на плоскость, которая ортогональна оси вращения спутника. На Рис.2 схематически показано, как были бы направлены эти разности ускорений и их вышеназванные проекции, а также указано – вправо
Рис.2
или влево, по отношению к вектору орбитальной скорости, было бы направлено ускорение бокового сноса. Направления «вправо» и «влево» зависят от направления вращения спутника, которое нам неизвестно – но можно видеть, что на перигейном и на апогейном «полу-витках» боковой снос должен происходить в противоположные стороны.
Результирующее ускорение бокового сноса (в м/с2), как функция времени, показано на Рис.3. Положительные значения соответствуют ускорению «влево», а отрицательные – ускорению «вправо». Результат двойного интегрирования по времени ускорения бокового сноса, т.е. линейный уход от расчётной траектории, показан на Рис.4 – где вся шкала
Рис.3
составляет 3000 км. Заметный здесь и далее дисбаланс для восходящего и нисходящего полувитков обусловлен тем, что на перигейном участке разность ускорений D a в среднем больше, чем на апогейном. Следует иметь в виду, что результаты на Рис.3,4 (и далее) получены при допущении, что фактор Qx (см. (2)) равен 0.03. Ниже мы уточним его значение.
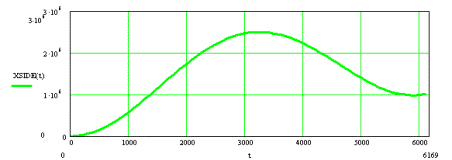
Рис.4
Боковой снос спутника даёт увеличение большой полуоси орбиты!
Хорошо известно [12], что боковое ускорение спутника приводит к повороту плоскости его орбиты. Но если бы у Эксплорера-1, из-за бокового сноса, плоскость орбиты несколько повернулась на восходящем участке, а затем почти вернулась в начальное положение на нисходящем участке – без изменения высот апогея и перигея – то спутник сократил бы себе
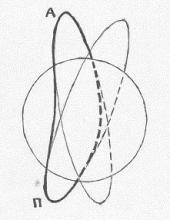
Рис.5
путь (см. схематический Рис.5), и его сигнал обнаружился бы не с опозданием, а с опережением. Для того, чтобы путь оказался удлинён, высоты апогея и перигея должны были увеличиться – а для этого боковой снос должен был приводить… к увеличению орбитальной скорости.
Но ведь так и должно быть! При сложении вектора начальной скорости V0 (см. Рис.6) и ортогонального ему вектора приращения скорости DV, результирующий вектор V1 является
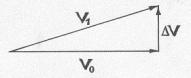
Рис.6
гипотенузой прямоугольного треугольника, и, конечно, ½ V1 ½>½ V0 ½. Можно возразить, что силовое воздействие, ортогональное вектору скорости, «не совершает работы», что оно только поворачивает вектор скорости, но не изменяет его величину – и привести хрестоматийный пример движения спутника по круговой орбите. Этот пример, на наш взгляд, крайне неудачен. Выше мы отмечали: при движении тела по круговой орбите, величина его орбитальной скорости постоянна потому, что здесь силовое воздействие на тело равно нулю, поскольку сила тяготения и центробежная сила уравновешивают друг друга. На эллиптической же орбите, когда эти силы не уравновешивают друг друга, не уравновешено и боковое силовое воздействие на вращающийся спутник, поэтому вектор его орбитальной скорости должен расти.
Итак, логическая цепочка в нашей задаче такова: увеличение времени полёта на первом витке определяется увеличением высот апогея и перигея, которые определяются увеличениями орбитальной скорости из-за ускорения бокового сноса спутника. Приращение большой полуоси A орбиты из-за тангенциального ускорения a q, которое, при малом эксцентриситете, почти сонаправлено с вектором орбитальной скорости и обеспечивает его рост, есть [12]
. (8)
Ускорение a q мы определяли как производную по времени от поправки D V к величине расчётной орбитальной скорости V orb из-за скорости бокового сноса V S:
, где 
, (9)
причём, V S находилась интегрированием ускорения бокового сноса a S (Рис.3). Полученная зависимость D V от времени приведена на Рис.7, в м/с, а зависимость a q - на Рис.8, в м/с2 –
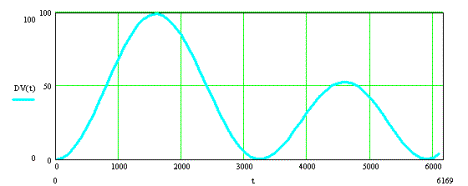
Рис.7
с инверсией знака производной на спадающих участках зависимости D V, поскольку боковой снос только увеличивает орбитальную скорость и, соответственно, только увеличивает большую полуось орбиты. Интегрирование, согласно (8), первого и четвёртого «горбов» функции на Рис.8 дало увеличения большой полуоси, соответственно, на 245 и 130 км. Таким
Рис.8
образом, для полного увеличения большой полуоси на первом витке мы получили (245+130)´2=750 км.
Теперь сопоставим этот результат с прямым расчётом приращения большой полуоси, через увеличение длительности витка. Для больших полуосей расчётной и «фактической» орбит Эксплорера-1, полученных на основе вышеприведённых апогейных и перигейных высот, период обращения (7) по расчётной орбите составляет, как уже отмечалось, 6169 с, а по фактической – 6874 с, т.е. на 11.8 мин больше. Из выражения (7) получаем:
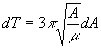. (10)
Учитывая, что на восходящем и нисходящем полувитках приращения большой полуоси различались в 0.53 раза, на основе (10) запишем
, (11)
где D T =11.8 мин, A 0=7271 км – большая полуось расчётной орбиты Эксплорера-1, D A – приращение большой полуоси на восходящем полувитке. Решение уравнения (11) относительно D A (средствами MathCAD) дало D A =359 км. Тогда для полного приращения большой полуоси на первом витке мы получаем 359´(1+0.53)=549 км. Этот результат прямого расчёта несколько меньше величины 750 км, полученной выше на основе модели бокового сноса спутника. Но это рассогласование можно устранить коррекцией множителя Qx (см. (2)), взятого равным 0.03, на коэффициент (549/750).
Наш модельный расчёт выполнен при ряде упрощающих допущений, и его точность невысока. Тем не менее, «аномалия Эксплорера», на наш взгляд, получила разумное объяснение.
Небольшое обсуждение.
Согласно вышеизложенному подходу, боковой снос быстро вращавшегося Эксплорера-1 и соответствующий рост орбитальной скорости происходили как на восходящем, так и на нисходящем участках траектории. Из-за этого траектория не могла быть замкнутой и, после первого витка, должна была продолжать свои эволюции, которые не укладывались в традиционные представления об орбитальном движении. «Сразу же после церемоний, связанных с запуском Explorer I, фон Браун начал писать и рассылать письма … очень выборочной группе «необычных физиков»… он явно искал «альтернативную физику», которая могла бы объяснить, что произошло с Explorer I на самом деле » [1]. Ведь, если вышеизложенный подход хотя бы в общих чертах верен, то апогей первого витка Эксплорера-1 находился над точкой земной поверхности, сдвинутой «вбок» от расчётной точки примерно на 1800 км, и такой же порядок имела ошибка по дальности, эквивалентная пятиминутному запаздыванию. Можно представить, какова была «точность» наведения первых межконтинентальных баллистических ракет США!
Следует добавить: наши расчёты сделаны при допущении, что угловая скорость вращения Эксплорера-1 оставалась постоянной. В действительности, она должна была уменьшаться – из-за преобразования энергии вращения в тепловую энергию через бегущие, в теле спутника, волны деформаций сжатия-растяжения. Поэтому вышеописанные эволюции орбиты Эксплорера-1 должны были ослабевать с каждым витком, и, после некоторого количества витков, орбита должна была стать, практически, стационарной.
Подчеркнём, что выше речь шла только о боковом сносе спутника, когда ось его вращения, практически, лежит в «плоскости орбиты» - в которой лежат радиус-вектор спутника и вектор его орбитальной скорости. Но ось вращения спутника может быть и ортогональна плоскости орбиты. Если спутник, при движении по эллиптической орбите, «кувыркается вперёд», то, по логике вышеизложенного, результирующая безопорная тяга должна тормозить его, а если спутник «кувыркается назад», то результирующая безопорная тяга должна ускорять его.В первом случае спутник с выключенными двигателями должен двигаться по скручивающейся траектории, а во втором – по раскручивающейся. По слухам, так и происходит – но публикаций об этом мы не нашли. Специалисты обычно помалкивают о том, чему они не нашли объяснения.
В завершени темы об «аномалии Эксплорера» следует уточнить, что безопорная тяга, которая появляется при вращении тела, свободно движущегося по не-круговой траектории, отнюдь не действует на планеты – хотя они движутся по эллиптическим орбитам вокруг Солнца и имеют собственные вращения. Опыт свидетельствует о том, что планеты покоятся в центрах своих областей тяготения, в которых солнечное тяготение «отключено» [8] (особый случай – Меркурий [13]). Вращение любого элемента объёма планеты происходит в постоянном «гравитационном потенциале». Значит, у планет отсутствуют вышеописанные деформации сжатия-растяжения, а потому равны нулю и ускорения бокового сноса.
Автор благодарит С.П.Гурьянова, В.Н.Тетерева и А.В.Толокнова за техническое содействие при подготовке эксперимента с вращающимся диском.
Ссылки.
1. Р.К.Хоагленд. Пятидесятилетний секрет фон Брауна. Веб-ресурс https://alexfl.ru/vechnoe/vechnoe_braun.html
2. В.Т.Волков, Д.А.Ягодников. Исследование и стендовая отработка ракетных двигателей на твёрдом топливе. «Изд-во МГТУ им. Н.Э.Баумана», М., 2007.
3. О первом искусственном спутнике Земли США. Веб-ресурс https://tvsh2004.narod.ru/1-isz3.html
4. В.И.Левантовский. Механика космического полёта в элементарном изложении. «Наука», М., 1974.
5. Т.М.Мелькумов, Н.И.Мелик-Пашаев, П.Г.Чистяков, А.Г.Шиуков. Ракетные двигатели. «Машиностроение», М., 1976.
6. Б.Т.Ерохин. Теория внутрикамерных процессов и проектирование РДТТ. «Машиностроение», М., 1991.
7. Газодинамические и теплофизические процессы в ракетных двигателях твёрдого топлива. Под ред. акад. А.С.Коротеева. «Машиностроение», М., 2004.
8. А.А.Гришаев. Книга «Этот «цифровой» физический мир». 2010.
9. А.А.Гришаев. Автономные превращения энергии квантовых пульсаторов – фундамент закона сохранения энергии.
10. А.А.Гришаев. Частотно-градиентная природа центробежных сил.
11. А.А.Гришаев. Сидерические вариации параметров орбит GPS: ещё одно подтверждение новой концепции тяготения.
12. К.Б.Алексеев, Г.Г.Бебенин, В.А.Ярошевский. Маневрирование космических аппаратов. «Машиностроение», М., 1970.
13. А.А.Гришаев. Тяготение Меркурия и проблема векового движения его перигелия.