1. Дайте определение функции. Что называется областью определения функции? Что называется графиком функции? Какие функции называются четными, нечетными, периодическими и какие особенности их графиков?
2. Начертите графики основных элементарных функций.
3. Сформулируйте определение предела функции при стремлении аргумента к конечному пределу и при стремлении аргумента к бесконечности.
4. Как связано понятие предела функции с понятиями ее пределов слева и справа?
5. Какая функция называется бесконечно малой и какие ее основные свойства?
6. Какая функция называется бесконечно большой и как она связана с бесконечно малой?
7. Сформулируйте основные теоремы о пределах.
8. Что такое первый и второй замечательные пределы?
9. Сформулируйте определения непрерывности функции в точке и на отрезке. Какие точки называются точками разрыва функции?
10. Сформулируйте определение производной. Каков ее механический и геометрический смысл?
11. Запишите формулы производных суммы, произведения, частного двух функций и таблицу производных.
12. Сформулируйте правило дифференцирования сложной функции и теорему о дифференцировании обратной функции.
13. Что такое логарифмическое дифференцирование?
14. Как находятся производные параметрически заданных функций?
15. Сформулируйте определение дифференциала функции. Каков его геометрический смысл?
16. В чем состоит правило Лопиталя для раскрытия неопределенностей?
17. Запишите формулу Тейлора с остаточным членом в форме Лагранжа в общем случае и для функций y=ex, y= sin x, y= cos x.
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ
Контрольная работа № 1
“Элементы аналитической геометрии и линейной алгебры”
Задача № 1
Даны координаты вершин пирамиды A1A2A3A4. Найти:
1) длину ребра A1A2;
2) угол между ребрами A1A2 и A1A4 ;
3) уравнение ребра A1A4, уравнение плоскости A1A2A3 и угол между ребром A1A4 и плоскостью A1A2A3;
4) уравнение высоты, опущенной из вершины A4 на грань A1A2A3;
5) площадь грани A1A2A3 и объем пирамиды;
6) показать, что векторы 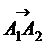 ,
, 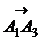 ,
, 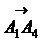 , образуют базис и найти координаты вектора
, образуют базис и найти координаты вектора  в этом базисе.
в этом базисе.
| Номер варианта | A1 | A2 | A3 | A4 |
| (4;0;3) | (1;  3;2) 3;2)
| (2;  4;5) 4;5)
| ( 1;8;2) 1;8;2)
| |
| 2 | (4;2;  3) 3)
| (2;1;0) | (1;2;  2) 2)
| (0;3;7) |
(5;  2;4) 2;4)
| (2;0;4) | (2;1;  1) 1)
| (8;2;  1) 1)
| |
| (0;2;7) | (2;3;1) | (3;2;4) | (2;  3;1) 3;1)
| |
(5;  1;0) 1;0)
| (3;2;2) | (2;  3;1) 3;1)
| (2;3;1) | |
| (3;4;1) | (-2;5;3) | ( 2;5;0) 2;5;0)
| (3;2;  1) 1)
| |
( 1;2;3) 1;2;3)
| (1;0;4) | ( 1;5;1) 1;5;1)
| (4;  2;3) 2;3)
| |
(4;  3;5) 3;5)
| (1;5;2) | (6;1;4) | (7;5;0) | |
| (4;1;3) | ( 1;0;5) 1;0;5)
| (6;2;3) | (2;2;  3) 3)
| |
(1;3;  5) 5)
| (1;  2;1) 2;1)
| (0;  2;3) 2;3)
| (2;3;1) | |
(5;  3;4) 3;4)
| (2;3;  1) 1)
| (3;2;0) | ( 1;2;5) 1;2;5)
| |
(4;0;  3) 3)
| (1;4;  2) 2)
| (5;2;3) | (3;2;4) | |
(2;  1;2) 1;2)
| ( 1;4;0) 1;4;0)
| (2;1;3) | (3;4;  2) 2)
| |
( 1;0;2) 1;0;2)
| (4;  4;1) 4;1)
| (2;6;3) | ( 2;5;4) 2;5;4)
| |
(2;  1;3) 1;3)
| ( 3;3;0) 3;3;0)
| (2;3;  1) 1)
| (1;2;  2) 2)
| |
| (3;2;1) | (4;4;  1) 1)
| ( 5;0;4) 5;0;4)
| (3;1;4) | |
(1;2;  3) 3)
| (4;0;2) | ( 2;4;5) 2;4;5)
| (0;4;3) | |
(1;3;  3) 3)
| (2;4;2) | (6;  3;0) 3;0)
| (2;1;3) | |
(2;3;  4) 4)
| ( 4;1;3) 4;1;3)
| (4;  2;5) 2;5)
| (0;3;2) | |
(0;  2;5) 2;5)
| ( 4;2;3) 4;2;3)
| (2;3;1) | (3;4;0) |
Задача № 2
. Даны координаты вершин треугольника ABC. Найти:
1) уравнения сторон AB, BC и их угловые коэффициенты;
2) тангенс угла АBC;
3) уравнение высоты CD и ее длину;
4) уравнение медианы AE и координаты точки K пересечения этой медианы с высотой CD.
Сделать чертеж.
| Номер варианта | А | В | С |
( 4;2) 4;2)
| (4;  4) 4)
| (8;8) | |
| 2 | (2;2) | ( 6; 6;  4) 4)
| ( 10;8) 10;8)
|
( 3,0) 3,0)
| (3;  6) 6)
| (9;6) | |
| (6;4) | ( 2; 2;  2) 2)
| ( 6;10) 6;10)
| |
( 3; 3;  1) 1)
| (3;5) | (9;  7) 7)
| |
| (4;2) | ( 4; 4;  4) 4)
| ( 8;8) 8;8)
| |
| (2;2) | ( 4; 4;  6) 6)
| (8;  10) 10)
| |
| (3,0) | ( 3; 3;  6) 6)
| ( 9;6) 9;6)
| |
( 6;4) 6;4)
| (2;  2) 2)
| (6;10) | |
(1;  3) 3)
| ( 5;3) 5;3)
| (7;9) | |
(2;  4) 4)
| ( 4; 4) 4; 4)
| (8;8) | |
( 2;2) 2;2)
| (4;  6) 6)
| ( 8; 8;  10) 10)
| |
( 3,0) 3,0)
| (3;6) | (9;  6) 6)
| |
| (4;6) | ( 2; 2;  2) 2)
| (10;  6) 6)
| |
( 1;-3) 1;-3)
| (5;3) | ( 7;9) 7;9)
| |
| (2;4) | ( 4; 4;  4) 4)
| (8;  8) 8)
| |
| (2;-2) | ( 6;4) 6;4)
| ( 10; 10;  8) 8)
| |
(0;  3) 3)
| ( 6;3) 6;3)
| (6;9) | |
(4;  6) 6)
| ( 2;2) 2;2)
| (10;6) | |
(3;  1) 1)
| ( 3;5) 3;5)
| ( 9; 9;  7) 7)
|
Задача № 3
Линия задана уравнением r = r (j) в полярной системе координат. Требуется:
1) построить линию по точкам от j =0 до j = p, придавая значения j через промежуток p /6;
2) найти уравнение линии в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось OX - с полярной осью;
3) определить вид линии по уравнению в декартовой системе координат;
4) сделать чертеж.
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 
7.  8.
8.  9.
9.  10.
10.  11.
11.  12.
12. 
13. 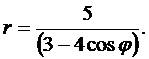 14.
14. 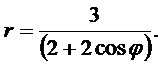 15.
15.  16.
16.  17.
17.  18.
18. 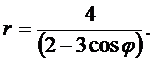
19.  20.
20. 
Задача № 4
Сделать чертеж и составить уравнение линии:
1) расстояние каждой точки которой до точки А (3; 0) втрое меньше расстояния ее до прямой х =  1;
1;
2) каждая точка которой находится вдвое дальше от точки А (3;0), чем от точки В ( 3; 0);
3; 0);
3) расстояние каждой точки которой до точки А (2; 0) вдвое меньше расстояния до точки В (8; 0);
4) каждая точка которой равноудалена от точки А (1;2) и от оси ОY;
5) для каждой точки которой сумма квадратов расстояний до точек А (−2;0) и В (2;,0) равна 40;
6) для каждой точки которой сумма квадратов расстояний до осей координат и до прямых х =2 и y =2 равна 6;
7) расстояние каждой точки которой до точки А (4; 0) втрое меньше расстояния ее до прямой х =  4;
4;
8) каждая точка которой находится втрое дальше от точки А (3;0), чем от точки В ( 1; 0);
1; 0);
9) расстояние каждой точки которой до точки А (2; 0) втрое меньше расстояния до точки В ( 6; 0);
6; 0);
4) каждая точка которой равноудалена от точки А (2;3) и от оси ОX;
11) для каждой точки которой сумма квадратов расстояний до точек А (−3;0) и В (3;0) равна 68;
12) для каждой точки которой сумма квадратов расстояний до осей координат и до прямых х =4 и y =−4 равна 24;
13) расстояние каждой точки которой до точки А ( 2; 0) вдвое меньше расстояния ее до прямой х =4;
2; 0) вдвое меньше расстояния ее до прямой х =4;
14) каждая точка которой находится вдвое дальше от точки А ( 3; 0), чем от точки В (6; 0);
3; 0), чем от точки В (6; 0);
15) расстояние каждой точки которой до точки А (1; 0) вдвое меньше расстояния до точки В (4; 0);
16) каждая точка которой равноудалена от точки А (5;2) и от оси ОY;
17) для каждой точки которой сумма квадратов расстояний до точек А (−1;0) и В (1;0) равна 20;
18) для каждой точки которой сумма квадратов расстояний до осей координат и до прямых х =−2 и y =−2 равна 6;
19) расстояние каждой точки которой до точки А (1; 0) вдвое меньше расстояния ее до прямой х =  5;
5;
20) каждая точка которой находится втрое дальше от точки А ( 3;0), чем от точки В (5; 0).
3;0), чем от точки В (5; 0).
Задача № 5
Решить системы линейных уравнений: а) методом Гаусса, б) методом Крамера и используя обратную матрицу.
1. а)  б)
б)  .
.
2. а)  б)
б) 
3. а)  б)
б)  .
.
4. а)  б)
б) 
5. а)  б)
б) 
6. а)  б)
б) 
7. а)  б)
б) 
8. а)  б)
б) 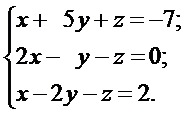
9. а)  б)
б) 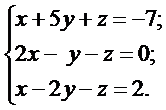
10. а)  б)
б) 
11. а) 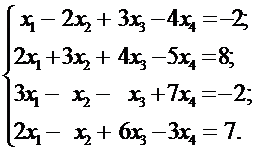 б)
б) 
12. а)  б)
б) 
13. а)  б)
б) 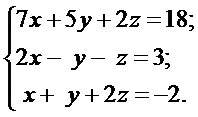
14. а)  б)
б) 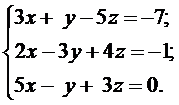
15. а)  б)
б) 
16. а)  б)
б) 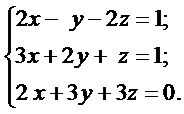
17. а)  б)
б) 
18. а)  б)
б) 
19. а)  б)
б) 
20. а)  б)
б) 
Контрольная работа № 2
“Введение в анализ. Техника дифференцирования”
Задача № 1
Найти пределы, не пользуясь правилом Лопиталя.
1. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
2. а)  ; б)
; б) 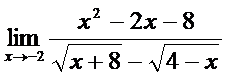 ;
;
в) 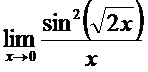 ; г)
; г) 
 ;
;
3. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
4. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
5. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
6. а) 
 ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
7. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
8. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
9. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
10. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
11. а)  ; б)
; б) 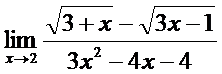 ;
;
в)  ; г)
; г) 
 ;
;
12. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
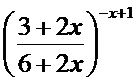 ;
;
13. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
14. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
15. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
16. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
17. а)  ; б)
; б)  ;
;
в) 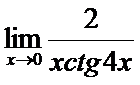 ; г)
; г) 
 ;
;
18. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
19. а) 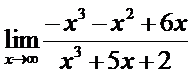 ; б)
; б) 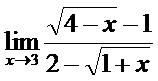 ;
;
в)  ; г)
; г) 
 ;
;
20. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
 ;
;
Задача № 2
Задана функция f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
1.  2.
2. 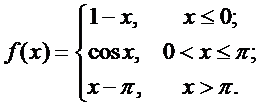
3.  4.
4. 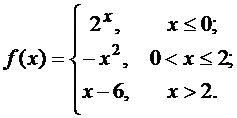
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
Задача № 3
Найти производные 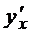 функций.
функций.
1. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ,
,
д) x tg y = y sin x.
2. а) 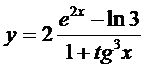 ; б)
; б)  ;
;
в)  ; г)
; г) 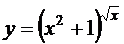 ;
;
д) (sin x) /y = (cos y) /x.
3. а)  ; б)
; б) 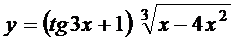 ;
;
в)  ; г)
; г)  ;
;
д) (x+y) sin x = cos y.
4. а)  ; б)
; б) 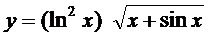 ;
;
в)  ; г)
; г) 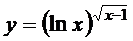 ;
;
д) x sin (x+y) = y.
5. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) y/x = sin (x 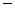 y).
y).
6. а)  ; б)
; б) 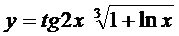 ;
;
в) 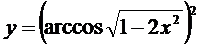 ; г)
; г)  ;
;
д) xy = sin (x+y).
7. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) x/y = ctg (x+y).
8. а)  ; б)
; б) 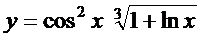 ;
;
в)  ; г)
; г)  ;
;
д) x cos y 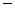 y sin x = 0.
y sin x = 0.
9. а) 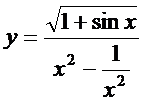 ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
10. а)  ; б)
; б)  ;
;
в) 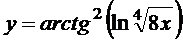 ; г)
; г)  ;
;
д)  .
.
11. а) 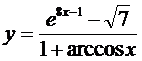 ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
12. а) 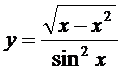 ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
13. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
14. а)  ; б)
; б)  ;
;
в) 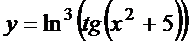 ; г)
; г) 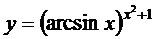 ;
;
д)  .
.
15. а)  ; б)
; б) 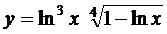 ;
;
в)  ; г)
; г)  ;
;
д)  .
.
16. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) cos(x-y)= x +2 y.
17. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
18. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
19. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
20. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) 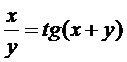 .
.
Задача 4
Найти производную второго порядка  от функции, заданной параметрически.
от функции, заданной параметрически.
1.  2.
2. 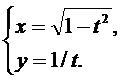 3.
3. 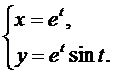
4.  5.
5.  6.
6. 
7.  8.
8.  9.
9. 
10.  11.
11.  12.
12. 
13. 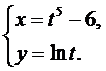 14.
14.  15.
15. 
16.  17.
17.  18.
18. 
19. 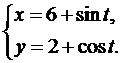 20.
20. 