Для металлов величина n является постоянной в широком интервале температур, поскольку определяется концентрацией атомов в кристалле.(n~1022-1025см-3). Средняя энергия свободных электронов в металлах, согласно квантовой механике (вырожденный электронный газ), является постоянной величиной, следовательно, V=const. Поэтому температурная зависимость удельного сопротивления может определяться лишь длиной свободного пробега l
Соответствующий квантовомеханический расчет дает, что в случае идеальной кристаллической решетки металла и при абсолютном нуле температуры Т=0К электроны проводимости не испытывали бы при своем движении никакого сопротивления. В этом случае практически отсутствует тепловое колебательное движение ионов кристаллической решетки и электроны движутся сквозь металл, не испытывая столкновений. При этом длина свободного пробега электронов l и удельная электропроводность металла s 
были бы бесконечно большими, а удельное сопротивление r® 0. Однако кристаллическая решетка никогда не бывает идеальной. Нарушения строгой периодичности решетки бывают обусловлены наличием атомов примеси или вакансий (т.е. отсутствием атома в узле решетки).
Кроме того, с повышением температуры ионы металла приходят в тепловое колебательное движение, нарушающее правильность кристаллической решетки. То сближаясь, то удаляясь друг от друга ионы создают «флуктуации» (изменения) плотности, на которых происходит рассеивание электронов. Чем выше температура, тем интенсивнее и чаще возникают флуктуации плотности кристаллической решетки и тем короче длина свободного пробега электрона. Квантовомеханический расчет показывает, что средняя длина свободного пробега электрона в кристалле обратно пропорциональна температуре:
(12)
Удельное электрическое сопротивление металлов можно представить в виде:
r=rкол+rпр (13)
где rкол - удельное сопротивление, обусловленное тепловыми колебаниями решетки, rпр - сопротивление, обусловленное рассеянием электронов на атомах примесей. Слагаемое rпр при небольшой концентрации примеси не зависит от температуры и образует так называемое остаточное сопротивление металла r0 при Т=0К.
Таким образом, выражение (10) с учетом (8) и (9) можно записать:
r=r0+aT (14)
где a - температурный коэффициент удельного сопротивления металла, r0 – остаточное удельное сопротивление металла.
Эта формула хорошо подтверждается экспериментом. В промышленности широко используются термометры сопротивления. Такой термометр представляет собой металлическую (обычно платиновую) проволочку, намотанную на фарфоровый или слюдяной каркас. После градуировки им можно измерять температуру с точностью несколько сотых долей градус в достаточно большом температурном интервале.
В полупроводниках температурная зависимость удельной проводимости обуславливается изменением концентрации носителей заряда (электронов и дырок), другие, вышеперечисленные механизмы, вносят вклад на много порядков меньше и ими можно пренебречь. Концентрация носителей заряда в полупроводнике зависит не только от температуры, а и от количества и типа примеси в нем. Рассмотрим три типа полупроводников:
1. Собственный полупроводник – не содержит посторонних примесей рис.5. Благодаря тепловому хаотическому движению при температурах больше нуля часть электронов переходит из валентной зоны в зону проводимости и становятся свободными. В валентной зоне образуются свободные от электронов места, которые могут двигаться под действием электрического тока как частицы с положительным зарядом (дырки). Число свободных электронов строго равно числу дырок.
Концентрация электронов и дырок зависит от температуры по экспоненциальному закону:
(15)
где DEg – ширина запрещенной зоны; k – постоянная Больцмана; Т – температура по шкале Кельвина; А – множитель, который можно считать постоянным, поскольку он слабо зависит от температуры по сравнению с экспонентой (A ~ T 3/2).
| |||
| Рис. 5 Энергетическая схема собственного полупроводника |
2. Полупроводник n-типа – содержит примесь, атомы которой имеют валентных электронов на один больше чем полупроводник. Например, кремний, основной материал современной микроэлектроники, имеет 4 валентных электрона, а фосфор, сурьма, мышьяк – 5. Четыре электрона примеси осуществляют валентные связи в кристалле, а пятый электрон имеет слабую связь с атомом, может легко перейти в зону проводимости рис.6. DEd – называется энергией ионизации донора. В результате электрический ток в полупроводнике n-типа определяется отрицательными зарядами (электронами). Такая примесь называется донорной. Обычно DЕd – сравнима и даже меньше энергии хаотического движения частиц при комнатной температуре (кТ), поэтому все доноры ионизованы. Такой полупроводник имеет ярко выраженный электронный тип проводимости.
| |||
| Рис.6 Энергетическая схема полупроводника n-типа |
3. Полупроводник Р – типа содержит акцепторную примесь. Атомы ее содержат валентных электронов на один меньше чем полупроводник. В кремнии - алюминий, галлий, индий. В кристалле атомы примеси образует энергетический уровень вблизи валентной зоны на расстоянии DEd рис.7. При температуре отличной от нуля на этот уровень будут переходить электроны из валентной зоны, образуя в ней подвижные дырки.
| |||
| Рис.7 Энергетическая схема полупроводника р-типа |
При температурах, близких к комнатной, энергия хаотического движения атомов кристалла kT сравнима с энергией ионизации донорной (DEd) или акцепторной (DEa) примесей. В результате примеси оказываются ионизованными. В полупроводниках n-типа концентрация электронов становится равной концентрации донорной примеси, а в р-типа концентрация дырок равна концентрации акцепторной примеси. При росте температуры концентрация носителей в примесном полупроводнике может в некотором интервале не зависеть от температуры, пока не станет проявляться собственная проводимость. Температура, при которой преобладает собственная проводимость, определяется шириной запрещенной зоны. Например, кремниевые полупроводниковые приборы могут работать до температур @120оС, (DEg=1,1эВ), а германиевые - @60оС. (DEg=0,7эВ). При достаточно низких температурах, (@70К) происходит деионизация доноров и акцепторов и концентрация носителей заряда уменьшается.
В собственном полупроводнике согласно (11) и (15) проводимость равна:
(16)
Поскольку подвижность электронов и дырок слабо зависит от температуры формулу (16) мы можем записать в виде:
(17)
где DEg – ширина запрещенной зоны; k – постоянная Больцмана; Т – температура по шкале Кельвина; s(T) – удельная электропроводность кристалла как функция температуры, s0 - начальная удельная электропроводность.
Прологарифмировав (17) получим:
(18)
График функции lns(T) от (
) представляет собой прямую линию (рис.8). Тангенс угла между данной прямой и осью абсцисс равен DEg./(2k). На этом и основан экспериментальный метод определения ширины запрещенной зоны полупроводников по измерению проводимости (сопротивления).
 |
Рис.8. Пример графика выражения (17) для расчета ширины
запрещенной зоны
Формула для расчета ширины запрещенной зоны на основании графика, представленного на рис.8, имеет следующий вид:
(19)
Точки 1 и 2 берутся на прямой (см. ниже). Для удобства расчета формулу (19) представим в виде:
(20)
где tgα определяется по формуле:
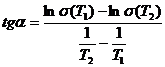(21)
На эксперименте определяется сопротивление образца R. Величина, обратная сопротивлению образца, называется электропроводностью: Σ=1/ R. При этом удельная электропроводность σ и электропроводность Σ связаны соотношением:
где S -площадь поперечного сечения образца, l - его длина. Отношение S/l изменяется незначительно при изменении температуры, поэтому σ и Σ отличаются постоянным множителем, не зависящим от температуры и в формулах (19 и 21) вместо σ можно использовать Σ:
(22)
(23)
На рис.9 представлена зависимость Σ от ()
 |
Рис.9. Пример графика для расчета ширины
запрещенной зоны по экспериментальным данным.
Величину tgα невозможно определить из графика путем измерения угла на графике. Для определения tgα вначале на график зависимости lnΣ(T) от () наносятся экспериментальные точки. Далее проводится прямая, наилучшим образом согласующаяся с этими точками в той области температур, где собственная проводимость значительно превышает примесную (50 ─ 1000С). При расчетах на компьютере используется метод наименьших квадратов. На усредненной прямой берутся точки 1 и 2 (см. рис.9). Для этих точек определяются lnΣ(T) и (), которые и подставляются в формулу (21).
Блок-схема установки приведена на рис.10.
Задание
1. Измерить зависимость сопротивления меди и германия от температуры. Измерения сопротивления проводить через каждые 5оС в области от комнатной температуры до 100оС. Полученные результаты занести в таблицу 1.
Таблица 1
| ToC | RCu, кОм | RGe, кОм |
На основании данных таблицы 1 построить графики зависимостей RCu(ToC) и RGe(ToC)
2. Определить ширину запрещенной зоны германия, для чего:
· Заполнить таблицу 2. В расчетных данных для Ln(ΣGe) и 1/T приводить три значащих цифры.
Таблица 2
| ToC | T, K | 1/T, K-1 | RCu, кОм | ΣGe, (кОм)-1 | Ln(ΣGe) |
· По данным таблицы 2 построить график зависимости lnΣ(T) от (), аналогичный представленному на рис.9.
· Для данных, соответствующих области 50-1000С, провести на графике усредненную прямую.
· Выбрать на прямой точки 1 и 2 и определить координаты этих точек.
· Определить тангенс угла наклона прямой по формуле (23).
· Рассчитать ширину запрещенной зоны германия по формуле (20). Значение постоянной Больцмана k = 1,38∙10-23 Дж/K
 |
Рис.10. Блок-схема установки
Литература
1. Савельев И. В. Курс общей физики, т. 3. М.: Наука и техника, 1989
2. Калашников С. Г. Электричество.- М.: Наука, 1977.