Решается задача расчета электромагнита, вписанного в сектор, развивающего максимальный момент деформации сектора гибкого якоря торцевого волнового шагового двигателя (ТВШД) при заданных величинах постоянного напряжения питания и перегрева обмотки.
1.1. Определение основных размеров ЭМ
Тяговое усилие двухполюсного электромагнита
(1.1.1)
где 
, Тл – магнитная индукция в воздушном зазоре, Sc, м2 – площадь сечения магнитопровода, 
Гн/м – магнитная проницаемость воздуха.
Магнитный поток
Вб (1.1.2)
С учетом (1.1.2)
Н. (1.1.3)
Пренебрегая потоками рассеяния и падением магнитного напряжения в магни-топроводе можно записать, что
, Вб, (1.1.4)
где 
- сила тока в А и число витков обмотки;
Магнитное сопротивление воздушного зазора
, (1.1.5)
где 
, м – суммарный воздушный зазор.
С учетом (1.1.4), (1.1.5)
Н (1.1.6)
Сила тока в обмотке
А, (1.1.7)
где 
, 
- плотность тока, 
- сечение обмоточного привода без изоляции.
Число витков обмотки
, (1.1.8)
где 
, 
- площадь окна под обмотку; 
- коэффициент заполнения окна медью.
С учетом (1.1.7), (1.1.8)
Н (1.1.9)
и момент деформации (изгибающий момент)
, (1.1.10)
где 
, м – плечо приложения силы F.
Из (1.1.10) видно, что момент прямо пропорционален 
. Рассмотрим подробнее эту величину.
На рис. 1.1.1 показаны размеры электромагнита, вписанного в сектор, образованный наружным диаметром Dн, внутренним диаметром Dвн и углом α.
Рис. 1.1.1 Размеры ЭМ
Из Рис. 1.1.1 можно записать, что:
Ширина полюса, м
, (1.1.11)
где 
и 
, 
- наружный и внутренний диаметры сектора,
, 
и 
, 
- ширина окна под обмотку и расстояние от внутреннего диаметра сектора до обмотки;
толщина полюса, 
, (1.1.12)
где 
- угол сектора;
высота окна под обмотку, 
(1.1.13)
где 
,
высота электромагнита,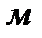 
|
|
, (1.1.14)
где 
, м – начальное значение немагнитного зазора между якорем ЭМ и сердечником.
Средний диаметр зубцовой зоны
, (1.1.15)
где 
- зазор по радиусу между наружным стержнем ЭМ и краем окна ГЯ, 
- выступ якоря, ЭМ для его крепления к ГЯ, 
- длина зубца (Рис. П3.2).
При перемещении зубца ГЯ на расстояние 
якорь ЭМ переместится на расстояние
, (1.1.16)
Где hз, м – высота зубца; δ0, м – начальное расстояние между вершинами зубцов.
Начальный немагнитный зазор якоря ЭМ
, (1.1.17)
где δк, м – конечный немагнитный зазор якоря ЭМ – толщина немагнитной прокладки между якорем и стержнями ЭМ.
Плечо приложения силы, 
(1.1.18)
площадь окна под обмотку
, 
(1.1.19)
площадь полюса
, (1.1.20)
где 
- коэффициент заполнения сердечника сталью.
Поясним как зависит 
от 
и 
С увеличением и 
произведение 
увеличивается. С увеличением 
, второй сомножитель в 
уменьшается, а третий – увеличивается, следовательно 
при изменении 
имеет максимум; при 
, 
имеет наибольшее значение, поэтому при изменении a и h, Sc имеет максимум. Координаты 
, 
максимума 
определяются из уравнений частных производных:
, (1.1.21)
; (1.1.22)
, (1.1.23)
. (1.1.24)
При изменении и , 
также будет иметь максимум, но его координаты 
, 
. C учетом проведенных расчетных исследований, координаты максимума 
можно приближенно определить по формуле:
, (1.1.25)
, (1.1.26)
где коэффициенты 
, 
.
С учетом найденных величин 
и 
, по вышеприведенным формулам определяют: 
(все размеры в системе СИ).
1.2. Электромагнитный расчет ЭМ
По найденным значениям и , заданным величинам напряжения питания 
, перегрева 
и изменении высоты окна 
под обмотку рассчитывают обмоточные данные, МДС обмотки, магнитную цепь с учетом падения МДС в магнитопроводе и потока рассеяния, магнитную индукцию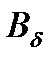 
, тяговое усилие 
и момент 
. Вы-брав максимальное значение 
определяют окончательно 
. Ниже приводятся и поясняются формулы, необходимые для вышеуказанной последовательности расчета.
|
|
Средний перегрев обмотки
(1.2.1)
где 
- коэффициент увеличения температуры внутри обмотки;
мощность потерь обмотки
, Вт (1.2.2)
где 
, А – сила тока обмотки;
коэффициент теплоотдачи при расчетной температуре 
Вт/м2 ºС; 
(1.2.3)
боковая поверхность обмотки
, (1.2.4)
где 
- начальное значение высоты окна под обмотку по (1.1.13) при 
;
- коэффициент теплоотдачи при 50ºС определяется по таблице 1.2.1
Таблица 1.2.1 коэффициенты теплоотдачи при 50ºС
 , Вт/м2 оС
| ||||
 , 
| 10-4 | 10-3 | 10-2 | 10-1 |
С учетом (1.2.1), (1.2.2) сила тока обмотки
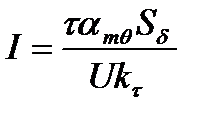, (1.2.5)
где перегрев обмоток при расчетной температуре θ и температуре окружаю-щего воздуха 
, оС (1.2.6)
Сопротивление обмотки при расчетной температуре
Ом (1.2.7)
с другой стороны
Ом (1.2.8)
где удельное электрическое сопротивление провода при температуре 
, (1.2.9)
средняя длина витка
м, (1.2.10)
W и Sпр, м2 – число витков и сечение провода обмотки по меди.
Из (1.2.8)
; (1.2.11)
с другой стороны
, (1.2.12)
где 
- коэффициент заполнения окна медью
С учетом (1.2.8), (1.2.12)
м2, (1.2.13)
где площадь окна
м2, (1.2.14)
Выбрав значение плотности тока 
A/м2 определяют сечение провода нулевого приближения
м2, (1.2.15)
округляют его до ближайшего большего стандартного значения и выбирают диаметры проводов без изоляции 
и с изоляцией 
по приложению 1.
|
|
Коэффициент заполнения окна медью при нулевом приближении
, (1.2.16)
где 
- коэффициент укладки
По (1.2.13) определяется сечение провода первого приближения 
, округляется до стандартного значения, выбираются 
и 
и по (1.2.16) 
. Если 
, то окончательно принимаются параметры провода первого приближения, по (1.2.12) – число витков и с учетом (1.2.5) – МДС обмотки 
.
Изгибающий момент ЭМ без учета магнитного насыщения стали и потока рассеяния
(1.2.17)
Начальное значение магнитной индукции в воздушном зазоре и якоре
Тл; (1.2.18)
С учетом насыщения и рассеяния 
выбирают на (5-10)% меньше 
. Магнитный поток в воздушном зазоре и якоря
Вб. (1.2.19)
Напряженность магнитного поля в воздушном зазоре
A/м. (1.2.20)
Напряженность магнитного поля в якоре 
при 
определяют по основной кривой намагничивания для выбранной марки стали по приложению 2.
Без учета падения МДС в магнитопроводе элементарный магнитный поток рассеяния через окно
(1.2.21)
Магнитный поток рассеяния
, Вб (1.2.22)
Магнитный поток в сердечнике
, Вб (1.2.23)
Магнитная индукция в сердечнике
, Тл (1.2.24)
По основной кривой намагничивания определяется напряженность магнитного поля в сердечнике 
, А/м.
По закону полного тока определяется МДС для создания выбранного значения 
.
А, (1.2.15)
где средние длины участков магнитопровода –сердечника и якоря:
м, (1.2.26)
м. (1.2.27)
Если 
, где 
- ранее найденная МДС при заданном перегреве обмотки 
, то корректируется выбранное значение 
и повторяется расчет магнитной цепи до совпадения обоих значений МДС.
Далее по (1.1.1) определяются тяговое усилие 
и изгибающий момент
(1.2.28)
Задавая другие значения 
в сторону увеличения проводят аналогичные расчеты, выбирают наибольший момент и соответствующее ему , 
, МДС и обмоточные данные.
Тяговое усилие 
и момент 
при конечном немагнитном зазоре 
определяются с учетом расчета магнитной цепи по найденному значению МДС при заданном перегреве обмотки.
Для начального немагнитного зазора 
и оптимального ЭМ рассчитывают:
индуктивность обмотки
Гн; (1.2.29)
электромагнитную постоянную времени
с; (1.2.30)
время такта
с; (1.2.31)
период следования импульсов напряжения (тока)
с, (1.2.32)
где 
- количество тактов коммутации фазы.
Для конечного немагнитного зазора 
аналогично рассчитывают 
, 
, 
.