Метод Симпсона (парабол)

Алгоритм вычисления определенного интеграла

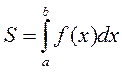
методом Симпсона с переменным шагом интегрирования.

 

§ Разбивается отрезок интегрирования на 2n равных частей с шагом h=(b-a)/(2n).

§ На каждом отрезке, состоящих из трех точек на интервалах [x₀,x₂], [x₂,x₄],…[x_2n-1,x_2n], подынтегральная функция f(x) заменяется параболой в виде интерполяционной формулы Ньютона: .

§ Суммируя интервалы, получим , где f₀ =f(a); f_2n = f(b); f_i - значение функции внутри отрезка.

§ Затем шаг интегрирования h уменьшается вдвое и производится оценка точности вычислений R двух последних циклов вычислений сумм площадей, которая сравнивается с величиной ε по условию R=|S_2n-S_n|/15<ε.

§ Процесс вычисления площадей повторяется, если R будет ложно.

 

 

Блок –схема метода Симпсона(парабол)

Составные части программы

Титульный лист программы

Находиться в Form 2.

Открывает программу и имеет кнопку входа в программу.

 

 

 

Главная форма программы

Главная форма программы расположена в Form1.

Начальные условие, т.е число разбиений n задается в объекте TextBox. С помощью объекта OptionButton организованы кнопки выбора метода вычисления.

Также в главной форме организовано простое меню.

Структура меню:

Меню

· Выход

График

Справка

· Блок схема метода трапеции

· Блок схема метода Симпсона

· Об авторе

· О программе

Исследование

Результат вычисления выводиться в объект PictureBox.

 

 

Form3.Визуализация метода

Для того, чтобы перейти в форму “Визуализация метода”, необходимо в меню главной формы выбрать вкладку График

При нажатии на кнопку «Построить график» на экран выводиться визуализация метода прямоугольников. Чтобы возвратиться в Главную форму, нужно нажать на кнопку «Назад».

 

Form4. Разработчик.

 

Чтобы открыть форму «Разработчик», нужно нажать:

Справка=> Об авторе.

При нажатии «Назад» происходит возврат в Главную форму.

 

 

Form5. Исследование методов.

При нажатии в меню Главной формы: Исследование появляется окно формы.

Если нажать кнопку «Построить» показывается результаты вычисления погрешностей методов.

 

Чтобы сохранить результаты исследования в текстовый файл,

имеется кнопка «Сохранить».

 

Form6. Блок-схема метода Симпсона

 

Чтобы открыть форму «Блок-схема метода Симпсона», нужно нажать:

Справка=>Блок-схема метода Симпсона

При нажатии «Назад» происходит возврат в Главную форму.

 

Form7. Блок-схема метода трапеции

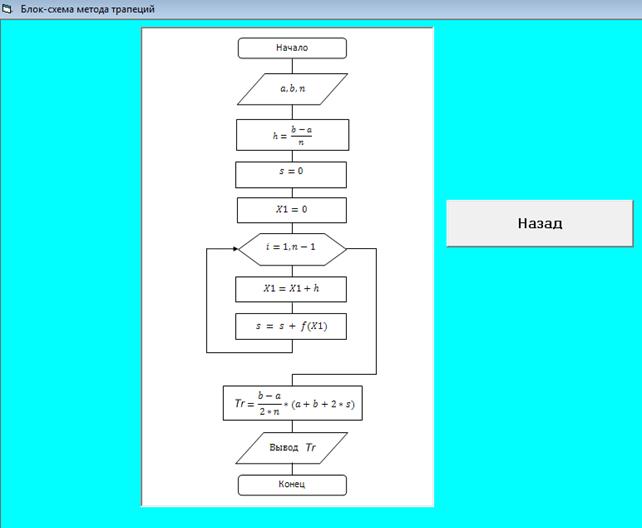
Чтобы открыть форму «Блок-схема метода трапеции», нужно нажать:

Справка=> Блок-схема метода трапеции.

При нажатии «Назад» происходит возврат в Главную форму

 

 

Form8. О программе

 

 

Чтобы открыть форму «О программе», нужно нажать:

Справка=> О программе.

При нажатии «Назад» происходит возврат в Главную форму.

 

 

Список литературы

1. Информатика: Учебник. – 3-е перераб. Изд. /под ред. Проф. Макаровой.- Финансы и статистика, 2000. -768 с.:ил.

2. Ананьев А.И., Федоров А.Ф. Самоучитель Visual Basic 6.0 – БХБ – Петербург, 2005. – 624 с.: ил.

3. Карчевская М.П., Рамбургер О.Л., Бикмеев А.Т. Лабораторный практикум по дисциплине «Информатика» -Уфимский Государственный Авиационный Технический Университет, Кафедра ИИ, Версия 0.8 beta; Уфа-2007.

4. Измерение и представление информации: Практикум по дисциплине «Информатика». Часть 1/ Уфимск. гос. авиац. техн. ун-т; Сост.: М.П. Карчевская, О.Л. Рамбургер.- Уфа, 2007.-27с

 

Приложения

Текст программы

Form1

Private Sub avtor_Click()

Form4.Show

Form1.Hide

End Sub

 

Private Sub Command1_Click()

n = Val(Text3)

a = Val(Text1)

b = Val(Text2)

Picture1.Cls

If Option1.Value Then

h = (b - a) / n

s = 0

x = a

For i = 1 To n - 1

x = x + h

y = f(x)

s = s + y

Next

trap = (2 * s + f(a) + f(b)) / 2 * h

Picture1.Print trap

End If

If Option2.Value Then

n1 = 2 * n

h = (b - a) / n1

s = 0

x = a

C = 1

For i = 1 To n1 - 1

x = x + h

y = x ^ x * (1 + Log(x))

s = s + (3 + C) * y

C = -C

Next

simp = h * (f(a) + f(b) + s) / 3

Picture1.Print simp

End If

If Option3.Value Then

s = f1(b) - f1(a)

Picture1.Print s

End If

End Sub

 

 

Private Sub exit_Click()

End

End Sub

 

Private Sub grafic_Click()

Form3.Show

Form1.Hide

End Sub

 

Private Sub isl_Click()

Form5.Show

Form2.Hide

End Sub

 

Private Sub prog_Click()

Form8.Show

Form1.Hide

End Sub

 

Private Sub simps_Click()

Form7.Show

Form1.Hide

End Sub

 

Private Sub trape_Click()

Form6.Show

Form1.Hide

End Sub

Form2

Private Sub Command1_Click()

Form1.Show

Form2.Hide

End Sub

 

Form3

Private Sub Command1_Click()

ymin = f(a)

ymax = f(a)

Picture1.Cls

h = (b - a) / n

For x = a To b Step 0.5

If f(x) > ymax Then ymax = f(x)

If f(x) < ymin Then ymin = f(x)

Next

Picture1.Scale (a - 0.5, ymax + 0.5)-(b + 0.5, ymin - 3)

For x = a To b Step 0.01

Picture1.PSet (x, f(x))

Next

For z = a To b + h Step h

Picture1.CurrentX = z - 0.01

Picture1.CurrentY = -0.01

Picture1.Print Format(z, "0.01")

Next z

 

Picture1.Line (a, f(a))-(b + h, f(a))

Picture1.Line (a, f(a))-(a, f(b))

s = 0

X1 = a

X0 = X1

For i = 1 To n

X1 = X1 + h

s1 = f(X0)

s = f(X1)

Picture1.Line (X0, 1)-(X0, s1), vbGreen

Picture1.Line (X1, 1)-(X1, s), vbGreen

X0 = X1

Next

End Sub

 

 

Private Sub Command2_Click()

Form1.Show

Form3.Hide

End Sub

Form4

Private Sub Command1_Click()

Form4.Hide

Form1.Show

End Sub

 

 

Form5

Picture1.Scale (0, 130)-(215, -5)

Picture1.Line (0, 0)-(215, 0)

Picture1.Line (10, 0)-(10, 200)

 

 

Ni_Li = f1(b) - f1(a)

For n = 10 To 200 Step 10

n1 = 2 * n

h = (b - a) / n1

s = 0

x = a

For i = 1 To n1 - 1

x = x + h

s = s + (3 + C) * f(x)

C = -C

Next

simp = h * (f(a) + f(b) + s) / 3

R(1, n / 10) = Abs(Ni_Li - simp)

Picture2.Print Format(R(1, n / 10), "0.00001")

Next

 

For n = 10 To 200 Step 10

h = (b - a) / n

s = 0

x = a

For i = 1 To n - 1

x = x + h

y = f(x)

s = s + y

Next

trap = (2 * s + f(a) + f(b)) / 2 * h

R(2, n / 10) = Abs(Ni_Li - trap)

Picture3.Print Format(R(2, n / 10), "0.000001")

Next

 

For i = 10 To 200

Picture1.Line (i, R(2, i / 10) * 100)-(i + 1, R(2, (i + 1) / 10) * 100), vbGreen

Picture1.Line (i, R(1, i / 10) * 100)-(i + 1, R(1, (i + 1) / 10) * 100), vbRed

Next

For d = 10 To 130 Step 10

Picture1.Line (8, d)-(10, d)

Picture1.Print d

Next

n = 10

For i = 0 To 20

Picture1.Line (n, 0)-(n, -2)

Picture1.Print n

If n = 200 Then Exit For

n = n + 10

Next

End Sub

 

Private Sub Command2_Click()

Form1.Show

Form5.Hide

End Sub

 

Private Sub Command3_Click()

CommonDialog1.ShowSave

Open CommonDialog1.FileName For Output As #1

For n = 10 To 200 Step 10

Print #1, "При числе разбиений равным" + Str(n) + vbCrLf; "погрешность вычисления методом Симпсона (парабол) равна " + Str(R(1, n / 10)) + vbCrLf; "погрешность методом трапеции равна" + Str(R(3, n / 10)) + vbCrLf;

Next

Close #1

End Sub

 

Private Sub CommonDialog2_Click()

 

End Sub

Form6

Private Sub Command1_Click()

ymin = f(a)

ymax = f(a)

Picture1.Cls

h = (b - a) / n

For x = a To b Step 0.5

If f(x) > ymax Then ymax = f(x)

If f(x) < ymin Then ymin = f(x)

Next

Picture1.Scale (a - 0.5, ymax + 0.5)-(b + 0.5, ymin - 0.5)

For x = a To b Step 0.01

Picture1.PSet (x, f(x)), vbRed

Next

For i = a To b + h Step h

Picture1.CurrentX = -0.01

Picture1.CurrentY = y - 0.01

Picture1.Print i

Next

Picture1.Line (a, f(a))-(b + h, f(a))

s = 0

X1 = a

X0 = X1

For i = 1 To n

X1 = X1 + h

s1 = f(X0)

s = f(X1)

Picture1.Line (X0, 1)-(X0, s1)

Picture1.Line (X0, s1)-(X1, s)

Picture1.Line (X1, 1)-(X1, s)

X0 = X1

Next

End Sub

 

Private Sub Command2_Click()

Form6.Hide

Form1.Show

End Sub

Form7

 

Private Sub Command1_Click()

Form7.Hide

Form1.Show

End Sub

Form8

Private Sub Command1_Click()

Form8.Hide

Form1.Show

End Sub